Graphs & Trees & Heaps
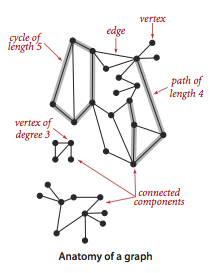
- A graph is a set of vertices and a collection of edges that each connect a pair of vertices.
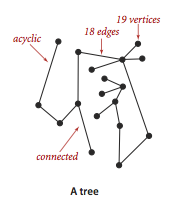
- A tree is an acyclic connected graph. A disjoint set of trees is called a forest.
- A spanning tree of a connected graph is a subgraph that contains all of that graph’s vertices and is a single tree.
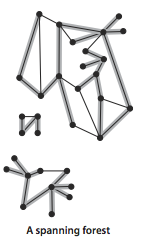
- A spanning forest of a graph is the union of spanning trees of its connected components.
- A tree is a data structure composed of nodes: A root node, and has zero or more child nodes. Each child node has zero or more child nodes.
- A binary tree is a tree in which each node has up to two children. A binary search tree is a binary tree which every node fits a specific ordering property: All left descendents <= n < all right descendents.
- A binary heap (min-heap or max-heap) is a complete binary tree, takes O(n) to build a heap. insertion and deletion will both take O(log(n)) time.
- A trie (prefix tree) is a variant of a binary tree (R-way tree) in which characters are stored at each node. Each path down the tree may represent a word. Tries Searching
 |
 |
 |
Graph Search
- The two most common ways to search a graph are depth-first search (DFS) and breadth-first search (BFS). DFS is often preferred if we want to visit every node in the graph. BFS is generally better if we want to find the shortest path (or just any path).
- Bidirectional search is used to find the shortest path between a source and destination node. It operates by essentially running two simultaneous BFS, one from each node. When their searches collide, we have found a path. The complexity reduces from O(k^d) to O(k^(d/2)).
- A directed graph (or digraph) is a set of vertices and a collection of directed edges that each connects an ordered pair of vertices.
- A directed acyclic graph (or DAG) is a digraph with no directed cycles.
- A minimum spanning tree (MST) of an edge-weighted graph is a spanning tree whose weight (the sum of the weights of its edges) is no larger than the weight of any other spanning tree. Prim’s or Kruskal’s algorithm computes the MST of any connected edge-weighted graph.
Construct Graph
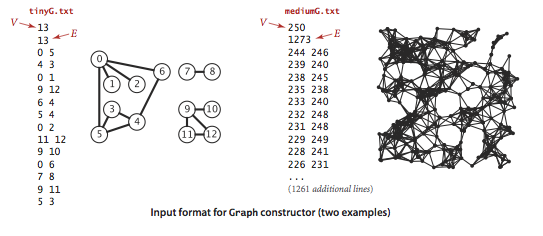
We use the adjacency-lists representation, where we maintain a vertex-indexed array of lists of the vertices connected by an each to each vertex.
  |
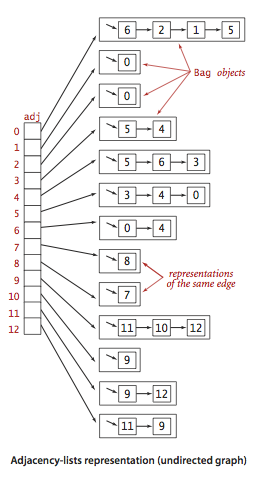 |
Construct Symbol Graph
Typical applications involve processing graphs using strings, not integer indices, to define and refer to vertices. We can use following data structure:
- A map table with String keys (vertex names) and int values (indices).
- An array keys[] that serves as an inverted index, giving the vertex name tied with each integer index.
- A Graph built using the indices to refer to vertices.
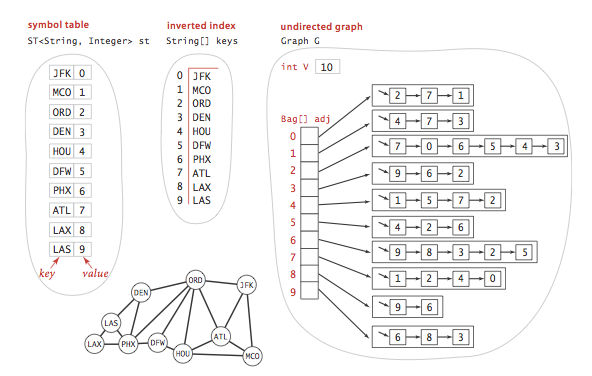
public class SymbolGraph {
private final String NEW_LINE = System.getProperty("line.separator");
private final int numVertices;
private int numEdges;
private Map<String, Integer> map; // key -> index
private String[] keys; // index -> key, inverted array
private List<List<Integer>> adjacents;
public SymbolGraph(String filename, String delimiter) {
map = new HashMap<String, Integer>();
// First pass builds the index by reading strings to associate
// distinct strings with an index
try {
File file = new File(filename);
FileInputStream stream = new FileInputStream(file);
Scanner scanner = new Scanner(new BufferedInputStream(stream));
// first pass builds the index by reading vertex names
while (scanner.hasNextLine()) {
String[] a = scanner.nextLine().split(delimiter);
for (String value : a) {
if (!map.containsKey(value))
map.put(value, map.size());
}
}
// inverted index to get string keys in an array
keys = new String[map.size()];
for (String name : map.keySet()) {
keys[map.get(name)] = name;
}
numVertices = map.size();
// second pass builds the graph by connecting first vertex on each
// line to all others
this.numEdges = 0;
this.adjacents = new ArrayList<>(numVertices);
for (int v = 0; v < numVertices; v++) {
adjacents.add(new ArrayList<Integer>());
}
stream = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(stream));
while (scanner.hasNextLine()) {
String[] a = scanner.nextLine().split(delimiter);
int v = map.get(a[0]);
for (int i = 1; i < a.length; i++) {
int w = map.get(a[i]);
addEdge(v, w);
}
}
scanner.close();
} catch (Exception e) {
throw new IllegalArgumentException("Could not read " + filename, e);
}
}
public boolean contains(String key) {
return map.containsKey(key);
}
public int indexOf(String key) {
return map.get(key);
}
public String nameOf(int vertex) {
validateVertex(vertex);
return keys[vertex];
}
public int numVertices() {
return numVertices;
}
public int numEdges() {
return numEdges;
}
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
numEdges++;
adjacents.get(v).add(w);
adjacents.get(w).add(v);
}
public Iterable<Integer> adjacents(int v) {
validateVertex(v);
return adjacents.get(v);
}
public int degree(int v) {
validateVertex(v);
return adjacents.get(v).size();
}
private void validateVertex(int vertex) {
if (vertex < 0 || vertex >= numVertices)
throw new IllegalArgumentException("vertex " + vertex + " is not between 0 and " + (numVertices - 1));
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(numVertices + " vertices, " + numEdges + " edges " + NEW_LINE);
for (int v = 0; v < numVertices; v++) {
s.append(v + ": ");
for (int w : adjacents.get(v)) {
s.append(w + " ");
}
s.append(NEW_LINE);
}
return s.toString();
}
}
Degrees of Separation
One of the classic applications of graph processing is to find the degree of separation between two individuals in a social network.
We will take the movies.txt data to demonstrate the SymbolGraph and BreadFirstPaths to find shortest paths in graphs.
public class DegreesOfSeparation {
private static final int INFINITY = Integer.MAX_VALUE;
private boolean[] visited; // marked[v] = is there an s-v path
private int[] edgeTo; // edgeTo[v] = previous edge on shortest s-v path
private int[] indegrees; // indegrees[v] = number of edges shortest s-v path
public DegreesOfSeparation(SymbolGraph graph, int source) {
visited = new boolean[graph.numVertices()];
indegrees = new int[graph.numVertices()];
edgeTo = new int[graph.numVertices()];
validateVertex(source);
bfs(graph, source);
}
private void bfs(SymbolGraph graph, int source) {
Queue<Integer> queque = new LinkedList<Integer>();
for (int v = 0; v < graph.numVertices(); v++)
indegrees[v] = INFINITY;
indegrees[source] = 0;
visited[source] = true;
queque.offer(source);
while (!queque.isEmpty()) {
int v = queque.poll();
for (int w : graph.adjacents(v)) {
if (!visited[w]) {
edgeTo[w] = v;
indegrees[w] = indegrees[v] + 1;
visited[w] = true;
queque.offer(w);
}
}
}
}
public boolean hasPathTo(int v) {
validateVertex(v);
return visited[v];
}
/**
* Returns the number of edges in a shortest path between the source and target
*/
public int indegress(int vertex) {
validateVertex(vertex);
return indegrees[vertex];
}
public Iterable<Integer> pathTo(int vertex) {
validateVertex(vertex);
if (!hasPathTo(vertex))
return null;
Stack<Integer> path = new Stack<Integer>();
int x;
for (x = vertex; indegrees[x] != 0; x = edgeTo[x])
path.push(x);
path.push(x);
return path;
}
// throw an IllegalArgumentException unless {@code 0 <= v < V}
private void validateVertex(int vertex) {
int V = visited.length;
if (vertex < 0 || vertex >= V)
throw new IllegalArgumentException("vertex " + vertex + " is not between 0 and " + (V - 1));
}
public String getPathToTarget(SymbolGraph sg, String target) {
StringBuilder builder = new StringBuilder();
if (sg.contains(target)) {
int t = sg.indexOf(target);
if (hasPathTo(t)) {
for (int v : pathTo(t)) {
if (builder.length() > 0)
builder.append(" -> ");
builder.append(sg.nameOf(v));
}
} else {
builder.append(target).append(" not connected.");
}
} else {
builder.append(target).append(" not in database.");
}
return builder.toString();
}
public static void main(String[] args) {
SymbolGraph graph = new SymbolGraph("data/movies.txt", "/");
String sourceName = "Bacon, Kevin";
if (!graph.contains(sourceName)) {
System.out.println(sourceName + " not in database.");
return;
}
int source = graph.indexOf(sourceName);
DegreesOfSeparation bfs = new DegreesOfSeparation(graph, source);
String target = "Kidman, Nicole";
String result = bfs.getPathToTarget(graph, target);
String answer = "Kidman, Nicole -> Cold Mountain (2003) -> Sutherland, Donald (I) -> Animal House (1978) -> Bacon, Kevin";
assert result.equals(answer);
target = "Grant, Cary";
result = bfs.getPathToTarget(graph, target);
answer = "Grant, Cary -> Charade (1963) -> Matthau, Walter -> JFK (1991) -> Bacon, Kevin";
assert result.equals(answer);
target = "Richie, Chen";
result = bfs.getPathToTarget(graph, target);
answer = "Richie, Chen not in database.";
assert result.equals(answer);
}
}
Construct Digraph
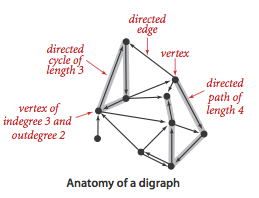 |
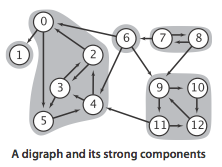 |
Compute MST
Kruskal’s algorithm processes the edges in order of their weight values (smallest to largest), taking for the MST (coloring black) each edge that does not form a cycle with edges previously added, stopping after adding V-1 edges. The black edges form a forest of trees that evolves gradually into a single tree, the MST (Minimum Spanning Tree).
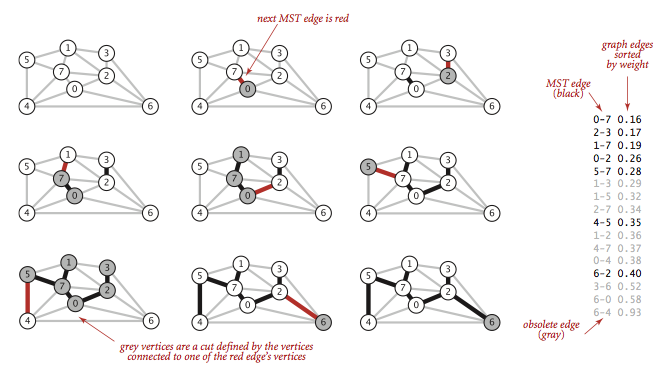
This implementation of Kruskal’s algorithm uses a queue to hold MST edges, a priority queue to hold edges not yet examined, and a union-find data structure for identifying ineligible edges.
public class KruskalMST {
private Queue<Edge> mst;
public KruskalMST(EdgeWeightedGraph G) {
mst = new Queue<Edge>();
MinPQ<Edge> pq = new MinPQ<Edge>();
for (Edge e : G.edges) {
pq.insert(e);
}
UionFind uf = new UF(G.V());
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
Edge e = pq.delMin();
int v = e.either(), w = e.other(v);
if (uf.connected(v, w)) continue;
uf.union(v, w);
mst.enqueue(e);
}
}
}
public class UnionFind {
private int[] parent; // parent[i] = parent of i
private byte[] rank; // rank[i] = rank of subtree rooted at i (never more than 31)
private int count; // number of components
public UnionFind(int n) {
if (n < 0)
throw new IllegalArgumentException();
count = n;
parent = new int[n];
rank = new byte[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 0;
}
}
public int find(int p) {
validate(p);
while (p != parent[p]) {
parent[p] = parent[parent[p]]; // path compression by halving
p = parent[p];
}
return p;
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
if (rank[rootP] < rank[rootQ])
parent[rootP] = rootQ;
else if (rank[rootP] > rank[rootQ])
parent[rootQ] = rootP;
else {
parent[rootQ] = rootP;
rank[rootP]++;
}
count--;
}
private void validate(int p) {
if (p < 0 || p >= parent.length)
throw new IllegalArgumentException();
}
}
Shortest Paths
- A shortest path from vertex s to vertex t is a directed path in a edge-weighted digraph, that no other path has a lower weight. The implementation is based on edge relaxation. The table below summarizes the 3 shortest-paths algorithms.
| algorithm | restriction | typical | worst-case | extra space | sweet spot |
|---|---|---|---|---|---|
| Dijkstra (eager) | positive edge weights | \(E\log V\) | \(E\log V\) | \(V\) | worst-case guarantee |
| topological order | edge-weighted DAGs | \(E + V\) | \(E + V\) | \(V\) | optimal for acyclic |
| Bellman-Ford (queue-based) | no negative cycles | \(E + V\) | \(EV\) | \(V\) | widely applicable |
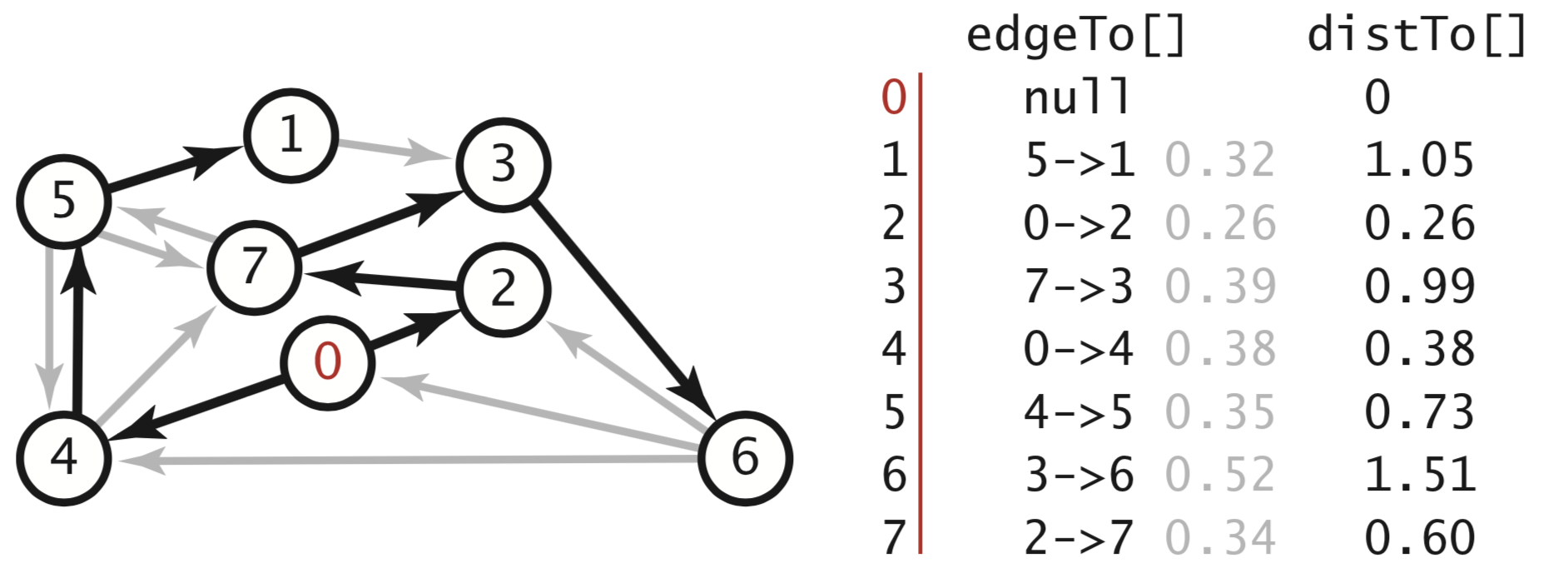
- Dijkstra’s algorithm solves the single-source shortest-paths problem in edge-weighted digraphs with nonnegative weights using extra space proportional to V and time proportional to E log V (in the worst case). It initializes dist[s] to 0 and all other distTo[] entries to positive infinity. Then, repeatedly relaxes and adds to the tree a non-tree vertex with the lowest distTo[] value, continuing until all vertices are on the tree or no non-tree vertex has a finite distTo[] value. We add a priority queue to keep track of vertices that are candidates for being the next to be relaxed. The visited[] array is not needed, because the lens[] or distTo[] is MAX_VALUE or POSITIVE_INFINITY.
- By relaxing vertices in topological order, we can solve the single-source shortest-paths problem for acyclic edge-weighted digraph (called edge-weighted DAG) in time proportional to E + V. It handles negative edge weights. Also, we can solve the single-source longest paths problems in edge-weighted DAGs by initializing the distTo[] values to negative infinity and switching the sense of the inequality in relax(); Or another way is to create a copy of the given edge-weighted DAG that all edge weights are negated, then just need to find the shortest path.
public AcyclicSP(EdgeWeightedDigraph G, int s) {
distTo = new double[G.V()];
edgeTo = new DirectedEdge[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
// visit vertices in topological order
Topological topological = new Topological(G);
if (!topological.hasOrder())
throw new IllegalArgumentException("Digraph is not acyclic.");
for (int v : topological.order()) {
for (DirectedEdge e : G.adj(v))
relax(e);
}
}
// relax edge e
private void relax(DirectedEdge e) {
int v = e.from(), w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
}
}
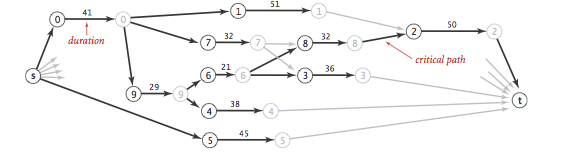
- The critical path method for parallel scheduling jobs is to proceed as follows:
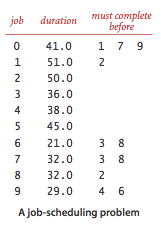 |
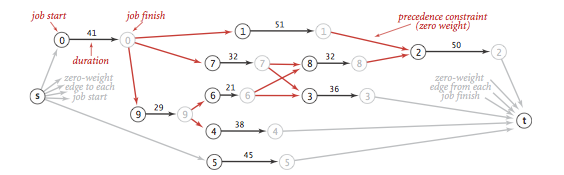  |
public static void main(String[] args) {
// number of jobs
int n = StdIn.readInt();
// start and end
int start = 2 * n;
int end = 2 * n + 1;
// build network
EdgeWeightedDigraph G = new EdgeWeightedDigraph(2 * n + 2);
for (int i = 0; i < n; i++) {
double duration = StdIn.readDouble();
G.addEdge(new DirectedEdge(start, i, 0.0));
G.addEdge(new DirectedEdge(i + n, end, 0.0));
G.addEdge(new DirectedEdge(i, i + n, duration));
// precedence constraints
int m = StdIn.readInt();
for (int j = 0; j < m; j++) {
int precedent = StdIn.readInt();
G.addEdge(new DirectedEdge(n + i, precedent, 0.0));
}
}
// compute longest path
AcyclicLP lp = new AcyclicLP(G, start);
}
- Shortest paths in general edge-weighted digraphs. A negative cycle is a directed cycle whose total weight (sum of the weights of its edges) is negative. The concept of a shortest path is meaningless if there is a negative cycle. Bellman-Ford algorithm with negative cycle detection can solve this problem.
- Queue-based Bellman-Ford algorithm is an effective and efficient method for solving the shortest paths problem even for the case when edge weights are negative.
public BellmanFordSP(EdgeWeightedDigraph G, int s) {
distTo = new double[G.V()];
edgeTo = new DirectedEdge[G.V()];
onQueue = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
queue = new Queue<Integer>();
queue.enqueue(s);
onQueue[s] = true;
while (!queue.isEmpty() && !hasNegativeCycle()) {
int v = queue.dequeue();
onQueue[v] = false;
relax(G, v);
}
assert check(G, s);
}
// relax vertex v and put other endpoints on queue if changed
private void relax(EdgeWeightedDigraph G, int v) {
for (DirectedEdge e : G.adj(v)) {
int w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if (!onQueue[w]) {
queue.enqueue(w);
onQueue[w] = true;
}
}
// check negative cycle after done V times calls/relaxes
if (cost++ % G.V() == 0) {
findNegativeCycle();
if (hasNegativeCycle()) return; // found a negative cycle
}
}
}
Maximum Flow
An st-flow (flow) is an assignment of values to the edges such that:
- Capacity constraint: 0 ≤ edge’s flow ≤ edge’s capacity.
- Local equilibrium: inflow = outflow at every vertex (except s and t).
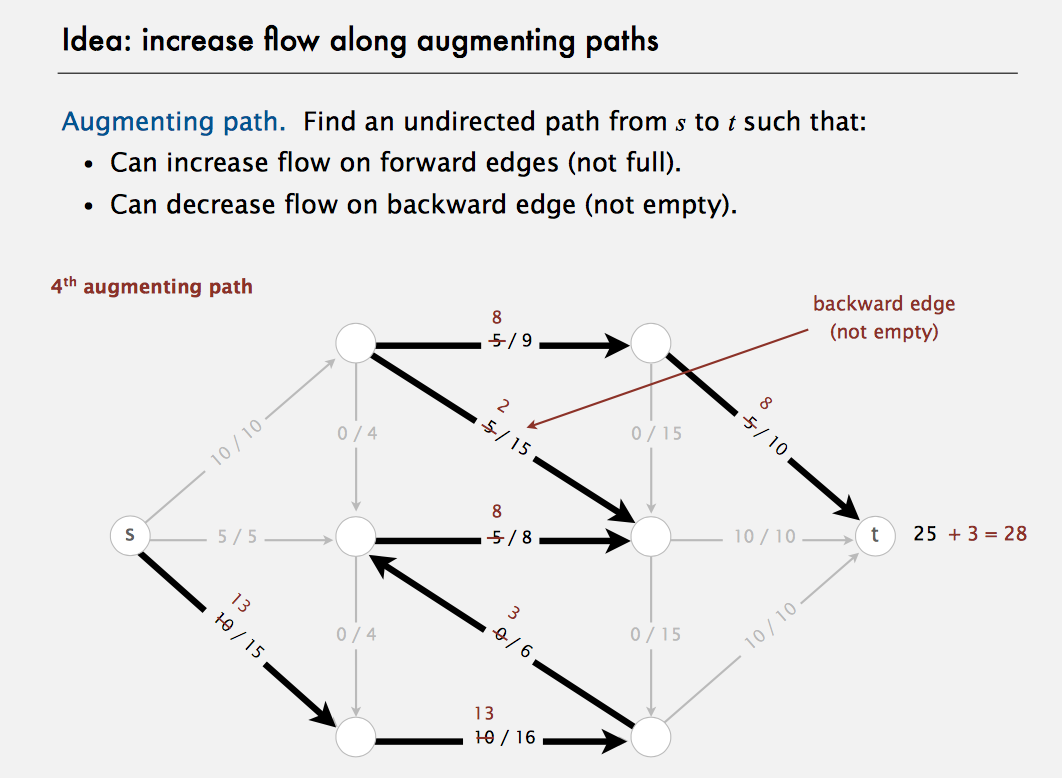
Ford-Fulkerson algorithm:
- Start with 0 flow.
While there exists an augmenting path:
- find an augmenting path
- compute bottleneck capacity
- increase flow on that path by bottleneck capacity
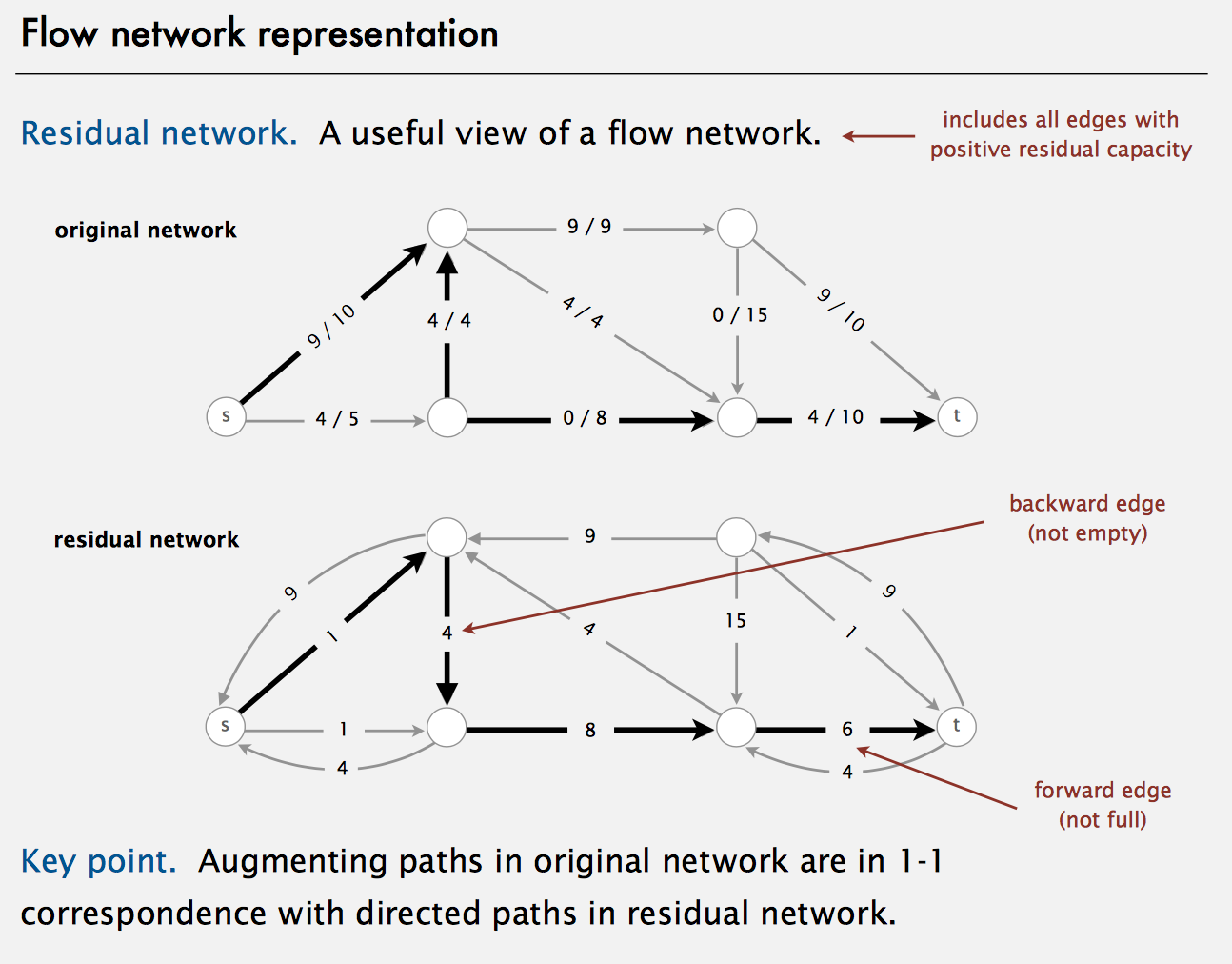
The shortest-augmenting-path implementation of the Ford-Fulkerson maxflow algorithm takes time proportional to EV(E+V) in the worst case. Bread-first search examines at most E edges and V vertices.
public class FordFulkerson {
private static final double FLOATING_POINT_EPSILON = 1E-11;
private final int V; // number of vertices
private boolean[] marked; // marked[v] = true if s->v path in residual graph
private FlowEdge[] edgeTo; // edgeTo[v] = last edge on shortest residual s->v path
private double value; // current value of max flow
/**
* Compute a maximum flow and minimum cut in the network {@code G} from vertex {@code s} to
* vertex {@code t}.
*/
public FordFulkerson(FlowNetwork G, int s, int t) {
V = G.V();
validate(s);
validate(t);
if (s == t)
throw new IllegalArgumentException("Source equals sink");
if (!isFeasible(G, s, t))
throw new IllegalArgumentException("Initial flow is infeasible");
// while there exists an augmenting path, use it
value = excess(G, t);
while (hasAugmentingPath(G, s, t)) {
// compute bottleneck capacity
double bottle = Double.POSITIVE_INFINITY;
for (int v = t; v != s; v = edgeTo[v].other(v)) {
bottle = Math.min(bottle, edgeTo[v].residualCapacityTo(v));
}
// augment flow
for (int v = t; v != s; v = edgeTo[v].other(v)) {
edgeTo[v].addResidualFlowTo(v, bottle);
}
value += bottle;
}
}
public double value() {
return value;
}
public boolean inCut(int v) {
validate(v);
return marked[v];
}
private void validate(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
// is there an augmenting path?
// if so, upon termination edgeTo[] will contain a parent-link representation of such a path
// this implementation finds a shortest augmenting path (fewest number of edges),
// which performs well both in theory and in practice
private boolean hasAugmentingPath(FlowNetwork G, int s, int t) {
edgeTo = new FlowEdge[G.V()];
marked = new boolean[G.V()];
// breadth-first search
Queue<Integer> queue = new LinkedList<Integer>();
queue.offer(s);
marked[s] = true;
while (!queue.isEmpty() && !marked[t]) {
int v = queue.poll();
for (FlowEdge e : G.adj(v)) {
int w = e.other(v);
// if residual capacity from v to w
if (e.residualCapacityTo(w) > 0) {
if (!marked[w]) {
edgeTo[w] = e;
marked[w] = true;
queue.offer(w);
}
}
}
}
// is there an augmenting path?
return marked[t];
}
// return excess flow at vertex v
private double excess(FlowNetwork G, int v) {
double excess = 0.0;
for (FlowEdge e : G.adj(v)) {
if (v == e.from())
excess -= e.flow();
else
excess += e.flow();
}
return excess;
}
// return excess flow at vertex v
private boolean isFeasible(FlowNetwork G, int s, int t) {
// check that capacity constraints are satisfied
for (int v = 0; v < G.V(); v++) {
for (FlowEdge e : G.adj(v)) {
if (e.flow() < -FLOATING_POINT_EPSILON || e.flow() > e.capacity() + FLOATING_POINT_EPSILON) {
System.err.println("Edge does not satisfy capacity constraints: " + e);
return false;
}
}
}
// check that net flow into a vertex equals zero, except at source and sink
if (Math.abs(value + excess(G, s)) > FLOATING_POINT_EPSILON) {
System.err.println("Excess at source = " + excess(G, s));
System.err.println("Max flow = " + value);
return false;
}
if (Math.abs(value - excess(G, t)) > FLOATING_POINT_EPSILON) {
System.err.println("Excess at sink = " + excess(G, t));
System.err.println("Max flow = " + value);
return false;
}
for (int v = 0; v < G.V(); v++) {
if (v == s || v == t)
continue;
else if (Math.abs(excess(G, v)) > FLOATING_POINT_EPSILON) {
System.err.println("Net flow out of " + v + " doesn't equal zero");
return false;
}
}
return true;
}
public class FlowNetwork {
private final int V;
private int E;
private Bag<FlowEdge>[] adj;
/**
* Initializes an empty flow network with {@code V} vertices and 0 edges.
*/
public FlowNetwork(int V) {
if (V < 0)
throw new IllegalArgumentException("Number of vertices in a Graph must be nonnegative");
this.V = V;
this.E = 0;
adj = (Bag<FlowEdge>[]) new Bag[V];
for (int v = 0; v < V; v++)
adj[v] = new Bag<FlowEdge>();
}
public int V() {
return V;
}
public int E() {
return E;
}
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
public void addEdge(FlowEdge e) {
int v = e.from();
int w = e.to();
validateVertex(v);
validateVertex(w);
adj[v].add(e);
adj[w].add(e);
E++;
}
public Iterable<FlowEdge> adj(int v) {
validateVertex(v);
return adj[v];
}
// return list of all edges - excludes self loops
public Iterable<FlowEdge> edges() {
Bag<FlowEdge> list = new Bag<FlowEdge>();
for (int v = 0; v < V; v++)
for (FlowEdge e : adj(v)) {
if (e.to() != v)
list.add(e);
}
return list;
}
}
class FlowEdge {
// to deal with floating-point roundoff errors
private static final double FLOATING_POINT_EPSILON = 1E-10;
private final int v; // from
private final int w; // to
private final double capacity; // capacity
private double flow; // flow
public FlowEdge(int v, int w, double capacity) {
if (v < 0)
throw new IllegalArgumentException("vertex index must be a non-negative integer");
if (w < 0)
throw new IllegalArgumentException("vertex index must be a non-negative integer");
if (!(capacity >= 0.0))
throw new IllegalArgumentException("Edge capacity must be non-negative");
this.v = v;
this.w = w;
this.capacity = capacity;
this.flow = 0.0;
}
public FlowEdge(FlowEdge e) {
this.v = e.v;
this.w = e.w;
this.capacity = e.capacity;
this.flow = e.flow;
}
public int from() {
return v;
}
public int to() {
return w;
}
public double capacity() {
return capacity;
}
public double flow() {
return flow;
}
/**
* Returns the endpoint of the edge that is different from the given vertex (unless the edge
* represents a self-loop in which case it returns the same vertex).
*/
public int other(int vertex) {
if (vertex == v)
return w;
else if (vertex == w)
return v;
else
throw new IllegalArgumentException("invalid endpoint");
}
/**
* Returns the residual capacity of the edge in the direction to the given {@code vertex}.
*/
public double residualCapacityTo(int vertex) {
if (vertex == v)
return flow; // backward edge
else if (vertex == w)
return capacity - flow; // forward edge
else
throw new IllegalArgumentException("invalid endpoint");
}
/**
* Increases the flow on the edge in the direction to the given vertex. If {@code vertex} is
* the tail vertex, this increases the flow on the edge by {@code delta}; if {@code vertex}
* is the head vertex, this decreases the flow on the edge by {@code delta}.
*/
public void addResidualFlowTo(int vertex, double delta) {
if (!(delta >= 0.0))
throw new IllegalArgumentException("Delta must be nonnegative");
if (vertex == v)
flow -= delta; // backward edge
else if (vertex == w)
flow += delta; // forward edge
else
throw new IllegalArgumentException("invalid endpoint");
// round flow to 0 or capacity if within floating-point precision
if (Math.abs(flow) <= FLOATING_POINT_EPSILON)
flow = 0;
if (Math.abs(flow - capacity) <= FLOATING_POINT_EPSILON)
flow = capacity;
if (!(flow >= 0.0))
throw new IllegalArgumentException("Flow is negative");
if (!(flow <= capacity))
throw new IllegalArgumentException("Flow exceeds capacity");
}
}
}
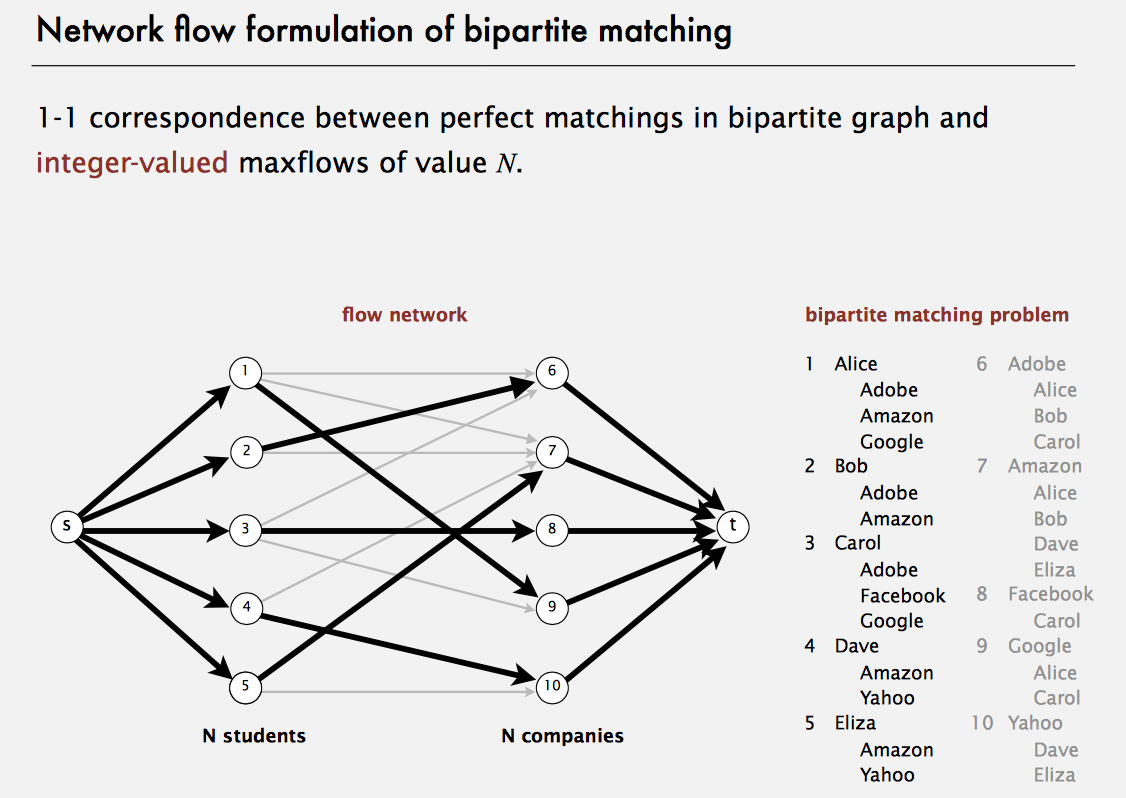
Bipartite Matching
A bipartite graph in a graph whose vertices can be partitioned into two disjoint sets such that every edge has one endpoint in either set. A perfect matching is a matching which matches all vertices in the graph.
This implementation uses the alternating path algorithm. It is equivalent to reducing to the maximum flow problem and running the augmenting path algorithm on the resulting flow network. The worst case is O((E+V)V)
Network flow formulation of bipartite matching:
- Create s, t, one vertex for each student, and one vertex for each job.
- Add edge from s to each student (capacity 1).
- Add edge from each job to t (capacity 1).
- Add edge from student to each job offered (infinity capacity).
public class BipartiteMatching {
private static final int UNMATCHED = -1;
private final int V; // number of vertices in the graph
private BipartiteX bipartition; // the bipartition
private int cardinality; // cardinality of current matching
private int[] mate; // mate[v] = w if v-w is an edge in current matching, = -1 if v is not in current matching
private boolean[] inMinVertexCover; // inMinVertexCover[v] = true if v is in min vertex cover
private boolean[] marked; // marked[v] = true if v is reachable via alternating path
private int[] edgeTo; // edgeTo[v] = w if v-w is last edge on path to w
/**
* Determines a maximum matching (and a minimum vertex cover) in a bipartite graph.
*/
public BipartiteMatching(Graph G) {
bipartition = new BipartiteX(G);
if (!bipartition.isBipartite()) {
throw new IllegalArgumentException("graph is not bipartite");
}
this.V = G.V();
// initialize empty matching
mate = new int[V];
for (int v = 0; v < V; v++)
mate[v] = UNMATCHED;
// alternating path algorithm
while (hasAugmentingPath(G)) {
// find one endpoint t in alternating path
int t = -1;
for (int v = 0; v < G.V(); v++) {
if (!isMatched(v) && edgeTo[v] != -1) {
t = v;
break;
}
}
// update the matching according to alternating path in edgeTo[] array
for (int v = t; v != -1; v = edgeTo[edgeTo[v]]) {
int w = edgeTo[v];
mate[v] = w;
mate[w] = v;
}
cardinality++;
}
// find min vertex cover from marked[] array
inMinVertexCover = new boolean[V];
for (int v = 0; v < V; v++) {
if (bipartition.color(v) && !marked[v])
inMinVertexCover[v] = true;
if (!bipartition.color(v) && marked[v])
inMinVertexCover[v] = true;
}
}
/*
* is there an augmenting path?
* - if so, upon termination adj[] contains the level graph;
* - if not, upon termination marked[] specifies those vertices reachable via an alternating
* path from one side of the bipartition
*
* an alternating path is a path whose edges belong alternately to the matching and not
* to the matching
*
* an augmenting path is an alternating path that starts and ends at unmatched vertices
*
* this implementation finds a shortest augmenting path (fewest number of edges), though there
* is no particular advantage to do so here
*/
private boolean hasAugmentingPath(Graph G) {
marked = new boolean[V];
edgeTo = new int[V];
for (int v = 0; v < V; v++)
edgeTo[v] = -1;
// breadth-first search (starting from all unmatched vertices on one side of bipartition)
Queue<Integer> queue = new LinkedList<Integer>();
for (int v = 0; v < V; v++) {
if (bipartition.color(v) && !isMatched(v)) {
queue.offer(v);
marked[v] = true;
}
}
// run BFS, stopping as soon as an alternating path is found
while (!queue.isEmpty()) {
int v = queue.poll();
for (int w : G.adj(v)) {
// either (1) forward edge not in matching or (2) backward edge in matching
if (isResidualGraphEdge(v, w) && !marked[w]) {
edgeTo[w] = v;
marked[w] = true;
if (!isMatched(w))
return true;
queue.offer(w);
}
}
}
return false;
}
// is the edge v-w a forward edge not in the matching or a reverse edge in the matching?
private boolean isResidualGraphEdge(int v, int w) {
if ((mate[v] != w) && bipartition.color(v))
return true;
if ((mate[v] == w) && !bipartition.color(v))
return true;
return false;
}
/**
* Returns the vertex to which the specified vertex is matched in the maximum matching computed
* by the algorithm.
*/
public int mate(int v) {
validate(v);
return mate[v];
}
/**
* Returns true if the specified vertex is matched in the maximum matching computed by the
* algorithm.
*/
public boolean isMatched(int v) {
validate(v);
return mate[v] != UNMATCHED;
}
/**
* Returns the number of edges in a maximum matching.
*/
public int size() {
return cardinality;
}
/**
* Returns true if the graph contains a perfect matching. That is, the number of edges in a
* maximum matching is equal to one half of the number of vertices in the graph (so that every
* vertex is matched).
*/
public boolean isPerfect() {
return cardinality * 2 == V;
}
/**
* Returns true if the specified vertex is in the minimum vertex cover computed by the
* algorithm.
*/
public boolean inMinVertexCover(int v) {
validate(v);
return inMinVertexCover[v];
}
private void validate(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
class BipartiteX {
private static final boolean WHITE = false;
private boolean isBipartite; // is the graph bipartite?
private boolean[] color; // color[v] gives vertices on one side of bipartition
private boolean[] marked; // marked[v] = true if v has been visited in DFS
private int[] edgeTo; // edgeTo[v] = last edge on path to v
private Queue<Integer> cycle; // odd-length cycle
/**
* Determines whether an undirected graph is bipartite and finds either a bipartition or an
* odd-length cycle.
*/
public BipartiteX(Graph G) {
isBipartite = true;
color = new boolean[G.V()];
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V() && isBipartite; v++) {
if (!marked[v]) {
bfs(G, v);
}
}
assert check(G);
}
private void bfs(Graph G, int s) {
Queue<Integer> q = new LinkedList<>();
color[s] = WHITE;
marked[s] = true;
q.offer(s);
while (!q.isEmpty()) {
int v = q.poll();
for (int w : G.adj(v)) {
if (!marked[w]) {
marked[w] = true;
edgeTo[w] = v;
color[w] = !color[v];
q.offer(w);
} else if (color[w] == color[v]) {
isBipartite = false;
// to form odd cycle, consider s-v path and s-w path
// and let x be closest node to v and w common to two paths
// then (w-x path) + (x-v path) + (edge v-w) is an odd-length cycle
// Note: distTo[v] == distTo[w];
cycle = new LinkedList<Integer>();
Stack<Integer> stack = new Stack<Integer>();
int x = v, y = w;
while (x != y) {
stack.push(x);
cycle.offer(y);
x = edgeTo[x];
y = edgeTo[y];
}
stack.push(x);
while (!stack.isEmpty())
cycle.offer(stack.pop());
cycle.offer(w);
return;
}
}
}
}
/**
* Returns true if the graph is bipartite.
*/
public boolean isBipartite() {
return isBipartite;
}
/**
* Returns the side of the bipartite that vertex {@code v} is on.
*/
public boolean color(int v) {
validateVertex(v);
if (!isBipartite)
throw new UnsupportedOperationException("Graph is not bipartite");
return color[v];
}
/**
* Returns an odd-length cycle if the graph is not bipartite, and {@code null} otherwise.
*/
public Iterable<Integer> oddCycle() {
return cycle;
}
private boolean check(Graph G) {
// graph is bipartite
if (isBipartite) {
for (int v = 0; v < G.V(); v++) {
for (int w : G.adj(v)) {
if (color[v] == color[w]) {
System.err.printf("edge %d-%d with %d and %d in same side of bipartition\n", v, w, v, w);
return false;
}
}
}
}
// graph has an odd-length cycle
else {
// verify cycle
int first = -1, last = -1;
for (int v : oddCycle()) {
if (first == -1)
Val first = v;
last = v;
}
if (first != last) {
System.err.printf("cycle begins with %d and ends with %d\n", first, last);
return false;
}
}
return true;
}
// throw an IllegalArgumentException unless {@code 0 <= v < V}
private void validateVertex(int v) {
int V = marked.length;
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
}
}
Graph Boot Camp
Flip A Boolean Matrix
Implement a routine that takes an n x m boolean array A together with an entry (x, y) and flips the color of the region associated with (x, y).
Let’s implement with DFS and BFS
// Deep-first Search
public static void flipColorDFS(List<List<Boolean>> A, int x, int y) {
final int[][] DIRS = new int[][] { { 0, 1 }, { 0, -1 }, { 1, 0 }, { -1, 0 } };
boolean color = A.get(x).get(y);
A.get(x).set(y, !color); // flip
for (int[] dir : DIRS) {
int nextX = x + dir[0], nextY = y + dir[1];
if (nextX >= 0 && nextX < A.size() && nextY >= 0 && nextY < A.get(nextX).size()
&& A.get(nextX).get(nextY) == color) {
flipColorDFS(A, nextX, nextY);
}
}
}
// Bread-first Search
public static void flipColorBFS(List<List<Boolean>> A, int x, int y) {
final int[][] DIRS = { { 0, 1 }, { 0, -1 }, { 1, 0 }, { -1, 0 } };
boolean color = A.get(x).get(y);
Queue<Point> queue = new LinkedList<>();
A.get(x).set(y, !A.get(x).get(y)); // flip
queue.add(new Point(x, y));
while (!queue.isEmpty()) {
Point curr = queue.element();
for (int[] dir : DIRS) {
Point next = new Point(curr.x + dir[0], curr.y + dir[1]);
if (next.x >= 0 && next.x < A.size() && next.y >= 0 && next.y < A.get(x).size()
&& A.get(next.x).get(next.y) == color) {
A.get(next.x).set(next.y, !color);
queue.add(next);
}
}
}
queue.remove();
}
Fill Enclosed Regions
Let A be a 2D array whose entries are either W or B, write a program that takes A, and replaces all Ws that can not reach the boundary with a B.
It is easier to focus on the inverse problem. Staring from outside and mark all the Ws (including neighbors) that can reach the boundary. Finally update other Ws.
public static void fillEnclosedRegions(List<List<Character>> board) {
// starting from first or last columns
for (int i = 0; i < board.size(); i++) {
if (board.get(i).get(0) == 'W')
markBoundaryRegion(i, 0, board);
if (board.get(i).get(board.get(i).size() - 1) == 'W')
markBoundaryRegion(i, board.get(i).size() - 1, board);
}
// starting from first or last rows
for (int j = 0; j < board.get(0).size(); j++) {
if (board.get(0).get(j) == 'W')
markBoundaryRegion(0, j, board);
if (board.get(board.size() - 1).get(j) == 'W')
markBoundaryRegion(board.size() - 1, j, board);
}
// marks the enclosed white regions as black
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board.size(); j++) {
board.get(i).set(j, board.get(i).get(j) != 'T' ? 'B' : 'W');
}
}
}
private static void markBoundaryRegion(int i, int j, List<List<Character>> board) {
Queue<Point> queue = new LinkedList<>();
queue.add(new Point(i, j));
while (!queue.isEmpty()) {
Point curr = queue.poll();
if (curr.x >= 0 && curr.x < board.size() && curr.y >= 0 && curr.y < board.get(curr.x).size()
&& board.get(curr.x).get(curr.y) == 'W') {
board.get(curr.x).set(curr.y, 'T');
queue.add(new Point(curr.x - 1, curr.y));
queue.add(new Point(curr.x + 1, curr.y));
queue.add(new Point(curr.x, curr.y + 1));
queue.add(new Point(curr.x, curr.y - 1));
}
}
}
Kill Process
Given n processes, each process has a unique PID (process id) and its PPID (parent process id).
Each process only has one parent process, but may have one or more children processes. This is just like a tree structure. Only one process has PPID that is 0, which means this process has no parent process. All the PIDs will be distinct positive integers.
We use two list of integers to represent a list of processes, where the first list contains PID for each process and the second list contains the corresponding PPID.
Now given the two lists, and a PID representing a process you want to kill, return a list of PIDs of processes that will be killed in the end. You should assume that when a process is killed, all its children processes will be killed. No order is required for the final answer.
Example 1:
Input:
pid = [1, 3, 10, 5]
ppid = [3, 0, 5, 3]
kill = 5
Output: [5,10]
Explanation:
3
/ \
1 5
/
10
Kill 5 will also kill 10.
HashMap + Breadth First Search or Depth First Search, Both O(n) complexity.
public static List<Integer> killProcess(List<Integer> pid, List<Integer> ppid, int kill) {
List<Integer> list = new ArrayList<>();
Map<Integer, List<Integer>> graph = new HashMap<>();
for (int i = 0; i < ppid.size(); i++) {
if (ppid.get(i) > 0) {
graph.putIfAbsent(ppid.get(i), new ArrayList<>());
graph.get(ppid.get(i)).add(pid.get(i));
}
}
// killProcessDfs(graph, kill, list);
killProcessBfs(graph, kill, list);
return list;
}
private static void killProcessDfs(Map<Integer, List<Integer>> graph, int kill, List<Integer> list) {
list.add(kill);
if (graph.containsKey(kill)) {
for (int next : graph.get(kill)) {
killProcessDfs(graph, next, list);
}
}
}
private static void killProcessBfs(Map<Integer, List<Integer>> graph, int kill, List<Integer> list) {
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(kill);
while (!queue.isEmpty()) {
int id = queue.poll();
list.add(id);
if (graph.containsKey(id)) {
for (int next : graph.get(kill)) {
queue.offer(next);
}
}
}
}
Deadlock Detection
One deadlock detection algorithm makes use of a “wait-for” graph: Processes are represented as nodes, and an edge from process P to Q implies P is waiting for Q to release its lock on the resource. A cycle in this graph implies the possibility of a deadlock.
Write a program that takes as input a directed graph and checks if the graph contains a cycle.
We can check for the existence of a cycle in graph by running DFS with maintaining a set of status. As soon as we discover an edge from a visiting vertex to a visiting vertex, a cycle exists in graph and we can stop.
The time complexity of DFS is O(V+E): we iterate over all vertices, and spend a constant amount of time per edge. The space complexity is O(V), which is the maximum stack depth.
public static boolean isDeadlocked(List<Vertex> graph) {
for (Vertex vertex : graph) {
if (vertex.state == State.UNVISITED && hasCycle(vertex)) {
return true;
}
}
return false;
}
private static boolean hasCycle(Vertex current) {
if (current.state == State.VISITING) {
return true;
}
current.state = State.VISITING;
for (Vertex next : current.edges) {
if (next.state != State.VISITED && hasCycle(next)) {
// edgeTo[next] = current; // if we need to track path
return true;
}
}
current.state = State.VISITED;
return false;
}
In a directed graph, we start at some node and every turn, walk along a directed edge of the graph. If we reach a node that is terminal, We say our starting node is eventually safe.
// This is a classic "white-gray-black" DFS algorithm
public List<Integer> eventualSafeNodes(int[][] graph) {
int N = graph.length;
int[] color = new int[N];
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < N; i++) {
if (hasNoCycle(i, color, graph))
ans.add(i);
}
return ans;
}
// colors: WHITE 0, GRAY 1, BLACK 2;
private boolean hasNoCycle(int node, int[] color, int[][] graph) {
if (color[node] > 0)
return color[node] == 2;
color[node] = 1;
for (int nei : graph[node]) {
if (color[nei] == 2)
continue;
if (color[nei] == 1 || !hasNoCycle(nei, color, graph))
return false;
}
color[node] = 2;
return true;
}
Clone A Graph
Design an algorithm that takes a reference to a vertex u, and creates a copy of the graph on the vertices reachable from u. Return the copy of u.
We recognize new vertices by maintaining a hash table mapping vertices in the original graph to their counterparts in the new graph.
public static Vertex cloneGraph(Vertex graph) {
if (graph == null)
return null;
Map<Vertex, Vertex> map = new HashMap<>();
Queue<Vertex> queue = new LinkedList<>();
queue.add(graph);
map.put(graph, new Vertex(graph.id));
while (!queue.isEmpty()) {
Vertex v = queue.remove();
for (Vertex e : v.edges) {
if (!map.containsKey(e)) {
map.put(e, new Vertex(e.id));
queue.add(e);
}
map.get(v).edges.add(map.get(e));
}
}
return map.get(graph);
}
Word Ladder
Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
Only one letter can be changed at a time. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
For example, Given:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]
As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
A transformation sequence is simply a path in Graph, so what we need is a shortest path from beginWord to endWord, by using two-end BFS, we can reduce the time complexity from O(n^k) -> O(2n^(k/2)), also use Trie in place of Set to break the loop as earlier as possible.
public class WordLadder {
// Two-end BFS, O(n^k) -> O(2n^(k/2))
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
Set<String> wordSet = new HashSet<>(wordList);
// confirm if word list must contain end word!
if (!wordSet.contains(endWord))
return 0;
int length = 1;
Set<String> beginSet = new HashSet<>();
Set<String> endSet = new HashSet<>();
beginSet.add(beginWord);
endSet.add(endWord);
while (!beginSet.isEmpty() && !endSet.isEmpty()) {
// always choose the smaller end
if (beginSet.size() > endSet.size()) {
Set<String> temp = beginSet;
beginSet = endSet;
endSet = temp;
}
Set<String> newSet = new HashSet<String>();
for (String word : beginSet) {
char[] chrs = word.toCharArray();
for (int i = 0; i < chrs.length; i++) {
char temp = chrs[i];
for (char c = 'a'; c <= 'z'; c++) {
chrs[i] = c;
String target = String.valueOf(chrs);
if (endSet.contains(target))
return length + 1;
if (wordSet.contains(target)) {
newSet.add(target);
wordSet.remove(target);
}
}
chrs[i] = temp;
}
}
beginSet = newSet;
length++;
}
return 0;
}
// Use Set O(n^k)
public int ladderLength2(String beginWord, String endWord, List<String> wordList) {
Set<String> set = new HashSet<>(wordList);
Queue<Ladder> queue = new LinkedList<>();
queue.offer(new Ladder(beginWord, 1));
while (!queue.isEmpty()) {
Ladder ladder = queue.poll();
char[] chrs = ladder.word.toCharArray();
for (int i = 0; i < chrs.length; i++) {
char temp = chrs[i];
for (char j = 'a'; j <= 'z'; j++) {
chrs[i] = j;
String target = new String(chrs);
if (set.contains(target)) {
if (target.equals(endWord))
return ladder.depth + 1;
queue.offer(new Ladder(target, ladder.depth + 1));
set.remove(target); // only use it once!
}
}
chrs[i] = temp;
}
}
return 0;
}
// Use Trie O(n^k), break loop as earlier as possible!
public int ladderLength3(String beginWord, String endWord, List<String> wordList) {
TrieNode trie = buildTrieTree(wordList);
Queue<Ladder> queue = new LinkedList<>();
queue.offer(new Ladder(beginWord, 1));
while (!queue.isEmpty()) {
Ladder ladder = queue.poll();
char[] chrs = ladder.word.toCharArray();
TrieNode node = trie;
for (int i = 0; node != null && i < chrs.length; i++) {
char temp = chrs[i];
for (char j = 'a'; j <= 'z'; j++) {
chrs[i] = j;
if (searchAndMark(node, chrs, i)) {
String target = new String(chrs);
if (target.equals(endWord))
return ladder.depth + 1;
queue.offer(new Ladder(target, ladder.depth + 1));
}
}
chrs[i] = temp;
node = node.next[temp - 'a'];
}
}
return 0;
}
private TrieNode buildTrieTree(List<String> words) {
TrieNode root = new TrieNode();
for (String word : words) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
int j = word.charAt(i) - 'a';
if (node.next[j] == null)
node.next[j] = new TrieNode();
node = node.next[j];
}
node.isWord = true;
}
return root;
}
private boolean searchAndMark(TrieNode node, char[] word, int start) {
for (int i = start; i < word.length; i++) {
node = node.next[word[i] - 'a'];
if (node == null)
return false;
}
boolean isWord = node.isWord;
node.isWord = false;
return isWord;
}
private class Ladder {
String word;
int depth;
Ladder(String word, int deep) {
this.word = word;
this.depth = deep;
}
}
class TrieNode {
boolean isWord = false;
TrieNode[] next = new TrieNode[26];
}
public static void main(String[] args) {
WordLadder solution = new WordLadder();
List<String> wordList = new ArrayList<>();
wordList.addAll(Arrays.asList("hot", "dot", "dog", "lot", "log", "cog"));
int steps = solution.ladderLength("hit", "cog", wordList);
System.out.println(steps);
assert steps == 5;
}
}
Word Ladder II
The same as above, find all shortest transformation sequence(s) from beginWord to endWord
Use Two-end recursion or iteration BFS, achieve the complexity O(2n^(k/2)).
// BFS
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> ladders = new ArrayList<>();
Set<String> wordSet = new HashSet<>(wordList);
if (!wordSet.contains(endWord))
return ladders;
// build the DAG graph using bidirectional BFS
Map<String, List<String>> graph = new HashMap<String, List<String>>();
if (!buildDAGbyBFS(beginWord, endWord, wordSet, graph)) {
return ladders;
}
// generate ladders by traversing the DAG graph
List<String> list = new ArrayList<>();
list.add(beginWord);
generateLadders(beginWord, endWord, graph, list, ladders);
return ladders;
}
private boolean buildDAGbyBFS(String beginWord, String endWord, Set<String> wordSet, Map<String, List<String>> graph) {
if (wordSet.contains(beginWord)) {
wordSet.remove(beginWord);
}
Set<String> beginSet = new HashSet<String>();
Set<String> endSet = new HashSet<String>();
beginSet.add(beginWord);
endSet.add(endWord);
boolean found = false;
boolean isForward = true;
while (!beginSet.isEmpty() && !endSet.isEmpty()) {
Set<String> newSet = new HashSet<String>();
// always choose the smaller set as begin set
if (beginSet.size() > endSet.size()) {
Set<String> temp = beginSet;
beginSet = endSet;
endSet = temp;
isForward = !isForward;
}
// clean up previous words
wordSet.removeAll(beginSet);
for (String word : beginSet) {
char[] chrs = word.toCharArray();
for (int i = 0; i < word.length(); i++) {
char old = chrs[i];
for (char c = 'a'; c <= 'z'; c++) {
chrs[i] = c;
if (old == c) {
continue;
}
String next = new String(chrs);
if (!wordSet.contains(next))
continue;
newSet.add(next);
String key = isForward ? word : next;
String value = isForward ? next : word;
graph.computeIfAbsent(key, k -> new ArrayList<>()).add(value);
if (endSet.contains(next))
found = true;
}
// backtrack
chrs[i] = old;
}
}
beginSet = newSet;
if (found) {
break;
}
}
return found;
}
// DFS
public List<List<String>> findLadders2(String beginWord, String endWord, List<String> wordList) {
List<List<String>> ladders = new ArrayList<>();
Set<String> wordSet = new HashSet<>(wordList);
if (!wordSet.contains(endWord))
return ladders;
Map<String, List<String>> graph = new HashMap<>(wordList.size());
Set<String> beginSet = new HashSet<>();
beginSet.add(beginWord);
Set<String> endSet = new HashSet<>();
endSet.add(endWord);
// build the DAG graph using bidirectional DFS
if (!buildDAGbyDFS(wordSet, beginSet, endSet, graph, true))
return ladders;
// generate ladders by traversing the DAG graph
List<String> list = new ArrayList<>();
list.add(beginWord);
generateLadders(beginWord, endWord, graph, list, ladders);
return ladders;
}
private boolean buildDAGbyDFS(Set<String> wordSet, Set<String> beginSet, Set<String> endSet, Map<String, List<String>> graph, boolean isForward) {
if (beginSet.isEmpty() || endSet.isEmpty())
return false;
wordSet.removeAll(beginSet);
boolean found = false;
Set<String> newSet = new HashSet<>();
for (String word : beginSet) {
char[] chrs = word.toCharArray();
for (int i = 0; i < chrs.length; i++) {
char old = chrs[i];
for (char c = 'a'; c <= 'z'; c++) {
if (old == c)
continue;
chrs[i] = c;
String next = new String(chrs);
if (!wordSet.contains(next))
continue;
newSet.add(next);
String key = isForward ? word : next;
String value = isForward ? next : word;
graph.computeIfAbsent(key, k -> new ArrayList<>()).add(value);
if (endSet.contains(next))
found = true;
}
// backtrack
chrs[i] = old;
}
}
if (found)
return true;
if (newSet.size() > endSet.size())
return buildDAGbyDFS(wordSet, endSet, newSet, graph, !isForward);
return buildDAGbyDFS(wordSet, newSet, endSet, graph, isForward);
}
private void generateLadders(String beginWord, String endWord, Map<String, List<String>> graph, List<String> path, List<List<String>> result) {
if (beginWord.equals(endWord)) {
result.add(new ArrayList<>(path));
} else if (graph.containsKey(beginWord)) {
for (String word : graph.get(beginWord)) {
path.add(word);
generateLadders(word, endWord, graph, path, result);
path.remove(path.size() - 1);
}
}
}
Can Tile
Small tile is 1 unit, Big tile is 5 units, given number of small tiles and big tiles, check whether we can tile the target.
public class Tile {
public static boolean canTile(int small, int big, int target) {
// return small >= (big * 5 > target ? target % 5 : target - big * 5);
return small >= (target / 5 > big ? target - big * 5 : target % 5);
}
public static boolean canTile2(int small, int big, int target) {
if (target == 0)
return true;
if (target < 0)
return false;
if (small == 0 && big == 0)
return false;
return (small > 0 && canTile2(small - 1, big, target - 1)) || (big > 0 && canTile2(small, big - 1, target - 5));
}
public static void main(String[] args) {
assert canTile(3, 4, 23) == canTile2(3, 4, 23);
assert canTile(3, 4, 24) == canTile2(3, 4, 24);
}
}
Sliding Puzzle
On a 2x3 board, there are 5 tiles represented by the integers 1 through 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it. The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].
Given a puzzle board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]
Think of this problem as a shortest path problem on a graph. Each node is a different board state, and we connect two boards by an edge if they can transformed into one another in one move. We can solve shortest path problems with breadth first search. There are (R*C)! possible board states, so the time and space complexity are both O(R*C*(R*C)!).
public int slidingPuzzle(int[][] board) {
int r = board.length, c = board[0].length;
int sr = 0, sc = 0;
search: for (sr = 0; sr < r; sr++)
for (sc = 0; sc < c; sc++)
if (board[sr][sc] == 0)
break search;
int[][] dirs = new int[][] { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } };
Queue<Node> queue = new ArrayDeque<>();
Node start = new Node(board, sr, sc, 0);
queue.add(start);
Set<String> visited = new HashSet<>();
visited.add(start.boardHash);
String target = Arrays.deepToString(new int[][] { { 1, 2, 3 }, { 4, 5, 0 } });
while (!queue.isEmpty()) {
Node node = queue.remove();
if (node.boardHash.equals(target))
return node.depth;
for (int[] dir : dirs) {
int neiR = dir[0] + node.zeroR;
int neiC = dir[1] + node.zeroC;
if (neiR < 0 || neiR >= r || neiC < 0 || neiC >= c)
continue;
int[][] newBoard = new int[r][c];
int t = 0;
for (int[] row : node.curBoard)
newBoard[t++] = row.clone();
newBoard[node.zeroR][node.zeroC] = newBoard[neiR][neiC];
newBoard[neiR][neiC] = 0;
Node nei = new Node(newBoard, neiR, neiC, node.depth + 1);
if (visited.contains(nei.boardHash))
continue;
queue.add(nei);
visited.add(nei.boardHash);
}
}
return -1;
}
class Node {
int[][] curBoard;
String boardHash;
int zeroR;
int zeroC;
int depth;
Node(int[][] curBoard, int zeroR, int zeorC, int depth) {
this.curBoard = curBoard;
this.zeroR = zeroR;
this.zeroC = zeorC;
this.depth = depth;
this.boardHash = Arrays.deepToString(curBoard);
}
}
Bus Routes
We have a list of bus routes. Each routes[i] is a bus route that the i-th bus repeats forever. For example if routes[0] = [1, 5, 7], this means that the first bus (0-th indexed) travels in the sequence 1->5->7->1->5->7->1->… forever. We start at bus stop S (initially not on a bus), and we want to go to bus stop T. Travelling by buses only, what is the least number of buses we must take to reach our destination? Return -1 if it is not possible.
Solution: Instead of thinking of the stops as vertex (of a graph), think of the buses as nodes. We want to take the least number of buses, which is a shortest path problem, conducive to using a breadth-first search.
public int numBusesToDestination(int[][] routes, int S, int T) {
if (S == T)
return 0;
int N = routes.length;
List<List<Integer>> graph = new ArrayList<>(N);
for (int i = 0; i < N; i++) {
Arrays.sort(routes[i]);
graph.add(new ArrayList<>());
}
// two buses are connected if they share at least one bus stop.
for (int i = 0; i < N - 1; i++) {
for (int j = i + 1; j < N; j++) {
if (intersect(routes[i], routes[j])) {
graph.get(i).add(j);
graph.get(j).add(i);
}
}
}
// breadth first search with queue
Set<Integer> visited = new HashSet<>();
Set<Integer> targets = new HashSet<>();
Queue<Vertex> queue = new ArrayDeque<>();
for (int i = 0; i < N; i++) {
if (Arrays.binarySearch(routes[i], S) >= 0) {
queue.offer(new Vertex(i, 0));
visited.add(i);
}
if (Arrays.binarySearch(routes[i], T) >= 0)
targets.add(i);
}
while (!queue.isEmpty()) {
Vertex vertex = queue.poll();
if (targets.contains(vertex.id))
return vertex.depth + 1;
for (Integer neighbor : graph.get(vertex.id)) {
if (!visited.contains(neighbor)) {
queue.offer(new Vertex(neighbor, vertex.depth + 1));
visited.add(neighbor);
}
}
}
return -1;
}
private boolean intersect(int[] routeA, int[] routeB) {
int i = 0, j = 0;
while (i < routeA.length && j < routeB.length) {
if (routeA[i] == routeB[j])
return true;
else if (routeA[i] < routeB[j])
i++;
else
j++;
}
return false;
}
public static void main(String[] args) {
BusRoutes solution = new BusRoutes();
int[][] routes = { { 1, 2, 7 }, { 3, 6, 7 }, { 6, 4, 5 } };
assert solution.numBusesToDestination(routes, 1, 5) == 3;
}
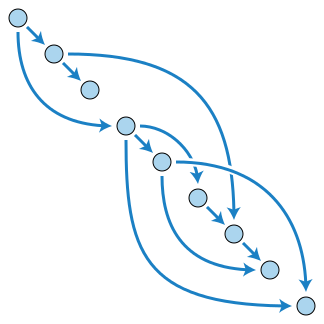
Topological Ordering
A topological ordering of a directed acyclic graph (DAG): every edge goes from earlier in the ordering (upper left) to later in the ordering (lower right). A directed graph is acyclic if and only if it has a topological ordering.
DAGs can be used to represent compilation operations, dataflow programming, events and their influence, family tree, version control, compact sequence data, binary decision diagram etc.
Let us practice it with the Course Schedule problem:
There are a total of n courses you have to take, labeled from 0 to n - 1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses.
There may be multiple correct orders, you just need to return one of them. If it is impossible to finish all courses, return an empty array.
For example:
2, [[1,0]]
There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is [0,1]
4, [[1,0],[2,0],[3,1],[3,2]]
There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3]. Another correct ordering is[0,2,1,3].
The problem turns out to find a topological sort order of the courses, which would be a DAG if it has a valid order. try BFS and DFS to resolve it! O(E+V)
public int[] findOrderInBFS(int numCourses, int[][] prerequisites) {
// initialize directed graph
int[] indegrees = new int[numCourses];
List<List<Integer>> adjacents = new ArrayList<>(numCourses);
for (int i = 0; i < numCourses; i++) {
adjacents.add(new ArrayList<>());
}
for (int[] edge : prerequisites) {
indegrees[edge[0]]++;
adjacents.get(edge[1]).add(edge[0]);
}
// breadth first search
int[] order = new int[numCourses];
Queue<Integer> toVisit = new ArrayDeque<>();
for (int i = 0; i < indegrees.length; i++) {
if (indegrees[i] == 0)
toVisit.offer(i);
}
int visited = 0;
while (!toVisit.isEmpty()) {
int from = toVisit.poll();
order[visited++] = from;
for (int to : adjacents.get(from)) {
indegrees[to]--;
if (indegrees[to] == 0)
toVisit.offer(to);
}
}
// should visited all courses
return visited == indegrees.length ? order : new int[0];
}
// track cycle with three states
public int[] findOrderInDFS(int numCourses, int[][] prerequisites) {
// initialize directed graph
List<List<Integer>> adjacents = new ArrayList<>(numCourses);
for (int i = 0; i < numCourses; i++) {
adjacents.add(new ArrayList<>());
}
for (int[] edge : prerequisites) {
adjacents.get(edge[1]).add(edge[0]);
}
int[] states = new int[numCourses]; // 0=unvisited, 1=visiting, 2=visited
Stack<Integer> stack = new Stack<>();
for (int from = 0; from < numCourses; from++) {
if (!topologicalSort(adjacents, from, stack, states))
return new int[0];
}
int i = 0;
int[] order = new int[numCourses];
while (!stack.isEmpty()) {
order[i++] = stack.pop();
}
return order;
}
private boolean topologicalSort(List<List<Integer>> adjacents, int from, Stack<Integer> stack, int[] states) {
if (states[from] == 1)
return false;
if (states[from] == 2)
return true;
states[from] = 1; // visiting
for (Integer to : adjacents.get(from)) {
if (!topologicalSort(adjacents, to, stack, states))
return false;
}
states[from] = 2; // visited
stack.push(from);
return true;
}
/**
* There are n different online courses numbered from 1 to n. You are given an array courses where
* courses[i] = [durationi, lastDayi] indicate that the ith course should be taken continuously for
* durationi days and must be finished before or on lastDayi.
*
* You will start on the 1st day and you cannot take two or more courses simultaneously.
*
* Return the maximum number of courses that you can take.
*
* Use priority queue can achieve time complexity: O(nlog(n)).
*/
public int scheduleCourseIII(int[][] courses) {
// It's always profitable to take the course with a smaller lastDay
Arrays.sort(courses, (a, b) -> a[1] - b[1]);
// It's also profitable to take the course with a smaller duration and replace the larger one.
Queue<int[]> queue = new PriorityQueue<>((a, b) -> b[0] - a[0]);
int daysUsed = 0;
for (int[] course : courses) {
if (daysUsed + course[0] <= course[1]) {
queue.offer(course);
daysUsed += course[0];
} else if (!queue.isEmpty() && queue.peek()[0] > course[0]) {
daysUsed += course[0] - queue.poll()[0];
queue.offer(course);
}
}
return queue.size();
}
/**
* There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You
* are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take
* course ai first if you want to take course bi.
*
* For example, the pair [0, 1] indicates that you have to take course 0 before you can take course
* 1. Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is
* a prerequisite of course c, then course a is a prerequisite of course c.
*
* You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should
* answer whether course uj is a prerequisite of course vj or not.
*
* Return a boolean array answer, where answer[j] is the answer to the jth query.
*/
public List<Boolean> scheduleCourseIV(int numCourses, int[][] prerequisites, int[][] queries) {
int[] indegrees = new int[numCourses];
List<List<Integer>> adjacents = new ArrayList<>(numCourses);
// Use BitSet to track the previous courses been taken
List<BitSet> previousCourses = new ArrayList<>(numCourses);
for (int i = 0; i < numCourses; i++) {
adjacents.add(new ArrayList<>());
previousCourses.add(new BitSet(numCourses));
}
for (int[] edge : prerequisites) {
indegrees[edge[1]]++;
adjacents.get(edge[0]).add(edge[1]);
}
Deque<Integer> toVisit = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegrees[i] == 0) {
toVisit.push(i);
}
}
while (!toVisit.isEmpty()) {
int index = toVisit.pop();
for (int v : adjacents.get(index)) {
previousCourses.get(v).set(index);
previousCourses.get(v).or(previousCourses.get(index));
indegrees[v]--;
if (indegrees[v] == 0) {
toVisit.push(v);
}
}
}
List<Boolean> result = new ArrayList<>(queries.length);
for (int[] query : queries) {
if (previousCourses.get(query[1]).get(query[0])) {
result.add(true);
} else {
result.add(false);
}
}
return result;
}
Alien Dictionary
There is a new alien language which uses the latin alphabet. However, the order among letters are unknown to you. You receive a list of non-empty words from the dictionary, where words are sorted lexicographically by the rules of this new language. Derive the order of letters in this language.
Example: Input: [ “wrt”, “wrf”, “er”, “ett”, “rftt”]; Output: “wertf”
This is another typical topological sorting problem.
public String alienOrder(String[] words) {
Map<Character, Set<Character>> map = new HashMap<>();
Map<Character, Integer> degree = new HashMap<>();
StringBuilder result = new StringBuilder();
for (String word : words) {
for (char c : word.toCharArray()) {
degree.put(c, 0);
}
}
for (int i = 0; i < words.length - 1; i++) {
String curr = words[i];
String next = words[i + 1];
for (int j = 0; j < Math.min(curr.length(), next.length()); j++) {
char c1 = curr.charAt(j);
char c2 = next.charAt(j);
if (c1 != c2) {
if (!map.containsKey(c1))
map.put(c1, new HashSet<>());
Set<Character> set = map.get(c1);
if (!set.contains(c2)) {
set.add(c2);
degree.put(c2, degree.getOrDefault(c2, 0) + 1);
}
break;
}
}
}
Queue<Character> queue = new LinkedList<>();
for (Map.Entry<Character, Integer> entry : degree.entrySet()) {
if (entry.getValue() == 0)
queue.add(entry.getKey());
}
while (!queue.isEmpty()) {
char c = queue.remove();
result.append(c);
if (map.containsKey(c)) {
for (char c2 : map.get(c)) {
degree.put(c2, degree.get(c2) - 1);
if (degree.get(c2) == 0)
queue.add(c2);
}
}
}
if (result.length() != degree.size())
result.setLength(0);
return result.toString();
}
Is Graph Bipartible?
Given an undirected graph, return true if and only if it is bipartite.
Recall that a graph is bipartite if we can split it’s set of nodes into two independent subsets A and B such that every edge in the graph has one node in A and another node in B.
The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice.
Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
Solution: Coloring by Depth-First Search, Time Complexity O(N+E), We explore each node once when we transform it from uncolored to colored, traversing all its edges in the process.
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] color = new int[n];
Arrays.fill(color, -1);
for (int start = 0; start < n; ++start) {
if (color[start] == -1) {
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(start);
color[start] = 0;
while (!queue.isEmpty()) {
Integer node = queue.poll();
for (int nei : graph[node]) {
if (color[nei] == -1) {
queue.offer(nei);
color[nei] = color[node] ^ 1;
} else if (color[nei] == color[node]) {
return false;
}
}
}
}
}
return true;
}
public static boolean isBipartible(Map<String, Set<String>> graph) {
Map<String, Integer> color = new HashMap<>();
for (String node : graph.keySet()) {
color.put(node, -1);
}
for (String start : graph.keySet()) {
if (color.get(start) == -1) {
Stack<String> stack = new Stack<>();
stack.push(start);
// We can always set to 0 because it starts with a new tree, not depends on other trees!
color.put(start, 0);
while (!stack.empty()) {
String node = stack.pop();
for (String nei : graph.get(node)) {
if (color.get(nei) == -1) {
stack.push(nei);
color.put(nei, color.get(node) ^ 1);
} else if (color.get(nei) == color.get(node)) {
return false;
}
}
}
}
}
return true;
}
// Another similar question to bipartite dislikes persons/parties
public static boolean possibleBipartition(int N, int[][] dislikes) {
// construct graph
@SuppressWarnings("unchecked")
List<Integer>[] graph = new ArrayList[N + 1];
for (int i = 1; i <= N; ++i)
graph[i] = new ArrayList<>();
for (int[] edge : dislikes) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
// coloring bipartites
Integer[] coloring = new Integer[N + 1];
for (int start = 1; start <= N; start++) {
if (coloring[start] == null) {
// use BFS
/*
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(start);
coloring[start] = 0;
while (!queue.isEmpty()) {
Integer node = queue.poll();
for (int nei : graph[node]) {
if (coloring[nei] == null) {
queue.offer(nei);
coloring[nei] = coloring[node] ^ 1;
} else if (coloring[nei].equals(coloring[node])) {
return false;
}
}
}
*/
// use DFS
if (!possibleBipartition(start, 0, graph, coloring))
return false;
}
}
return true;
}
public static boolean possibleBipartition(int node, int color, List<Integer>[] graph, Integer[] coloring) {
if (coloring[node] != null)
return coloring[node] == color;
coloring[node] = color;
for (int nei : graph[node])
if (!possibleBipartition(nei, color ^ 1, graph, coloring))
return false;
return true;
}
// The input can be Map<String, Collection<String>> dislikes
public boolean possibleBipartition(int N, int[][] dislikes) {
// construct graph
Map<Integer, Set<Integer>> graph = new HashMap<>();
for (int i = 1; i <= N; ++i)
graph.put(i, new HashSet<>());
for (int[] edge : dislikes) {
graph.get(edge[0]).add(edge[1]);
graph.get(edge[1]).add(edge[0]);
}
// coloring bipartites
Map<Integer, Integer> coloring = new HashMap<>();
for (int start : graph.keySet()) {
if (!coloring.containsKey(start)) {
// use BFS
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(start);
coloring.put(start, 0);
while (!queue.isEmpty()) {
Integer node = queue.poll();
for (int nei : graph.get(node)) {
if (!coloring.containsKey(nei)) {
queue.offer(nei);
coloring.put(nei, coloring.get(node) ^ 1);
} else if (coloring.get(nei).equals(coloring.get(node))) {
return false;
}
}
}
// use DFS
/*
if (!possibleBipartitionDfs(start, 0, graph, coloring))
return false;
*/
}
}
return true;
}
public boolean possibleBipartitionDfs(Integer node, Integer color, Map<Integer, Set<Integer>> graph, Map<Integer, Integer> coloring) {
if (coloring.containsKey(node))
return coloring.get(node).equals(color);
coloring.put(node, color);
for (int nei : graph.get(node)) {
if (!possibleBipartitionDfs(nei, color ^ 1, graph, coloring))
return false;
}
return true;
}
Sentence Similarity II
Given two sentences words1, words2 (each represented as an array of strings), and a list of similar word pairs pairs, determine if two sentences are similar.
For example, words1 = [“great”, “acting”, “skills”] and words2 = [“fine”, “drama”, “talent”] are similar, if the similar word pairs are pairs = [[“great”, “good”], [“fine”, “good”], [“acting”,”drama”], [“skills”,”talent”]].
Solution: Two words are similar if they are the same, or there is a path connecting them from edges represented by pairs.
We can check whether this path exists by performing a depth-first search from a word and seeing if we reach the other word. The search is performed on the underlying graph specified by the edges in pairs.
Time Complexity: O(NP), where N is the maximum length of words1 and words2, and P is the length of pairs. Each of N searches could search the entire graph. You can also use Union-Find search to achieve Time Complexity: O(NlogP+P).
private Map<String, String> parents = new HashMap<>();
public boolean areSentencesSimilarTwo(String[] sentence1, String[] sentence2, List<List<String>> similarPairs) {
if (sentence1.length != sentence2.length) {
return false;
}
for (List<String> list : similarPairs) {
union(list.get(0), list.get(1), parents);
}
for (int i = 0; i < sentence1.length; i++) {
if (!find(sentence1[i]).equals(find(sentence2[i]))) {
return false;
}
}
return true;
}
private void union(String s1, String s2, Map<String, String> roots) {
String ps1 = find(s1);
String ps2 = find(s2);
if (!ps1.equals(ps2)) {
roots.put(s2, ps1); // halve path
roots.put(ps2, ps1);
}
}
private String find(String s) {
while (parents.containsKey(s)) {
s = parents.get(s);
}
return s;
}
public boolean areSentencesSimilarTwo(String[] words1, String[] words2, String[][] pairs) {
if (words1.length != words2.length)
return false;
Map<String, List<String>> graph = new HashMap<>();
for (String[] pair : pairs) {
for (String word : pair) {
if (!graph.containsKey(word))
graph.put(word, new ArrayList<>());
}
graph.get(pair[0]).add(pair[1]);
graph.get(pair[1]).add(pair[0]);
}
Queue<String> queue = new ArrayDeque<>();
Set<String> visited = new HashSet<>();
for (int i = 0; i < words1.length; i++) {
queue.clear();
visited.clear();
queue.offer(words1[i]);
visited.add(words1[i]);
search: {
while (!queue.isEmpty()) {
String word = queue.poll();
if (word.equals(words2[i]))
break search;
if (graph.containsKey(word)) {
for (String nei : graph.get(word)) {
if (!visited.contains(nei)) {
queue.offer(nei);
visited.add(nei);
}
}
}
}
return false;
}
}
return true;
}
Shortest Distance from All Buildings
You want to build a house on an empty land which reaches all buildings in the shortest amount of distance. You can only move up, down, left and right. You are given a 2D grid of values 0, 1 or 2, where:
Each 0 marks an empty land which you can pass by freely. Each 1 marks a building which you cannot pass through. Each 2 marks an obstacle which you cannot pass through. Example:
Input: [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
1 - 0 - 2 - 0 - 1
| | | | |
0 - 0 - 0 - 0 - 0
| | | | |
0 - 0 - 1 - 0 - 0
Output: 7
Explanation: Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2),
the point (1,2) is an ideal empty land to build a house, as the total
travel distance of 3+3+1=7 is minimal. So return 7.
Time Complexity is O((number of 1)*(number of 0)) ~= O(m^2*n^2).
public int shortestDistance(int[][] grid) {
int dirs[][] = { { -1, 0 }, { 0, 1 }, { 1, 0 }, { 0, -1 } };
int rows = grid.length, cols = grid[0].length;
// Store total distance sum for each empty cell to all houses.
int[][] totalDist = new int[rows][cols];
int minDist = 0, emptyLandValue = 0;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
// Start a BFS from each house.
if (grid[row][col] == 1) {
// Reset min distance!
minDist = Integer.MAX_VALUE;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[] { row, col });
int steps = 0; // levels
while (!queue.isEmpty()) {
steps++;
// Iterator on in the same level
for (int i = queue.size(); i > 0; i--) {
int[] curr = queue.poll();
for (int[] dir : dirs) {
int nextRow = curr[0] + dir[0];
int nextCol = curr[1] + dir[1];
// For each cell with the value equal to empty land value,
// add distance and decrement the cell value by 1 in favor of tracking visited
if (nextRow >= 0 && nextRow < rows && nextCol >= 0 && nextCol < cols && grid[nextRow][nextCol] == emptyLandValue) {
grid[nextRow][nextCol]--;
totalDist[nextRow][nextCol] += steps;
queue.offer(new int[] { nextRow, nextCol });
minDist = Math.min(minDist, totalDist[nextRow][nextCol]);
}
}
}
}
// Abort if not found any empty land
if (minDist == Integer.MAX_VALUE) {
return -1;
}
// Decrement empty land value to be searched in next iteration.
emptyLandValue--;
}
}
}
return minDist;
}
Optimize Water Distribution in a Village
/**
* There are n houses in a village. We want to supply water for all the houses by building wells and
* laying pipes.
*
* For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the
* -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between
* houses are given by the array pipes, where each pipes[j] = [house1, house2, cost] represents the
* cost to connect house1 and house2 together using a pipe. Connections are bidirectional.
*
* Return the minimum total cost to supply water to all houses.
*
* Example 1:
*
*
* Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]] <br>
* Output: 3 <br>
* Explanation: The image shows the costs of connecting houses using pipes. The best strategy is to
* build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the
* total cost is 3.
*
* https://leetcode.com/problems/optimize-water-distribution-in-a-village/
*
* Solution: Convert it into a standard minimum spanning tree (MST) problem and use Prim's
* algorithm.
*
* Time Complexity: O((V+E)⋅log(V+E)); Space Complexity: O(V+E); V is vertices, E is edges.
*/
public class OptimizeWaterDistribution {
public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
// int[0] is house, int[1] is cost
Queue<int[]> queue = new PriorityQueue<>(n, (a, b) -> (a[1] - b[1]));
List<List<int[]>> graph = new ArrayList<>(n + 1);
for (int i = 0; i < n + 1; ++i) {
graph.add(new ArrayList<int[]>());
}
// Add a virtual vertex 0 for the insided wells cost,
for (int i = 0; i < wells.length; i++) {
int[] virtualEdge = { i + 1, wells[i] };
graph.get(0).add(virtualEdge);
queue.add(virtualEdge); // starts with well!
}
// Add the bidirectional edges to the graph
for (int[] pipe : pipes) {
graph.get(pipe[0]).add(new int[] { pipe[1], pipe[2] });
graph.get(pipe[1]).add(new int[] { pipe[0], pipe[2] });
}
Set<Integer> visited = new HashSet<>();
visited.add(0); // Already in queue
int totalCost = 0;
// n + 1 to cover the virtual vertex 0
while (visited.size() < n + 1) {
int[] edge = queue.poll();
if (visited.contains(edge[0])) {
continue;
}
visited.add(edge[0]);
totalCost += edge[1];
for (int[] neighbor : graph.get(edge[0])) {
if (!visited.contains(neighbor[0])) {
queue.add(neighbor);
}
}
}
return totalCost;
}
}
Binary Trees
- Recursive algorithm are well-suited to problems on trees. Remember to include space implicitly allocated on the function call stack when doing space complexity analysis.
- Let T be a binary tree of n nodes, with height h. Implemented recursively, these traversals have O(n) time complexity and O(h) additional space complexity. (The space complexity is dictated by the max depth of function call stack.) If each node has a parent field, the traversals can done with O(1) additional space complexity.
- Binary Tree Traversals:
- In-Order Traversal (left -> current -> right);
- Pre-Order Traversal (current -> left -> right);
- Post-Order Traversal (left -> right -> current);
Binary Tree Boot Camp
Height-Balanced Binary Tree
Given a binary tree, determine if it is height-balanced. A height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
public boolean isBalanced(TreeNode root) {
return checkBalanced(root) != Integer.MIN_VALUE;
}
private int checkBalanced(TreeNode root) {
if (root == null)
return -1; // base case
int lH = checkBalanced(root.left);
if (lH == Integer.MIN_VALUE)
return Integer.MIN_VALUE;
int rH = checkBalanced(root.right);
if (rH == Integer.MIN_VALUE)
return Integer.MIN_VALUE;
if (Math.abs(lH - rH) > 1)
return Integer.MIN_VALUE;
else
return Math.max(lH, rH) + 1;
}
Convert to Balanced BST
Given a BST which may be unbalanced. convert it into a balanced BST that has minimum possible height.
Input:
4
/
3
/
2
/
1
Output:
3 3 2
/ \ / \ / \
1 4 OR 2 4 OR 1 3 OR ..
\ / \
2 1 4
Input:
4
/ \
3 5
/ \
2 6
/ \
1 7
Output:
4
/ \
2 6
/ \ / \
1 3 5 7
The efficient solution with O(n) time is to in-order traverse the given BST and generate an array. Then build a balanced BST out of the sorted array.
public TreeNode convertToBalancedTree(TreeNode root) {
List<TreeNode> nodes = new ArrayList<>();
storeBSTNodes(root, nodes);
return buildBalancedTree(nodes, 0, nodes.size() - 1);
}
// in-order traverse
private void storeBSTNodes(TreeNode node, List<TreeNode> nodes) {
if (node == null)
return;
storeBSTNodes(node.left, nodes);
nodes.add(node);
storeBSTNodes(node.right, nodes);
}
// Convert sorted array to binary search tree (BST)
private TreeNode buildBalancedTree(List<TreeNode> nodes, int start, int end) {
if (start > end)
return null;
// get mid node and make it root
int mid = start + (end - start) / 2;
TreeNode node = nodes.get(mid);
// use index in in-order traverse
node.left = buildBalancedTree(nodes, start, mid - 1);
node.right = buildBalancedTree(nodes, mid + 1, end);
return node;
}
Self-Symmetric Binary Tree
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3
But the following [1,2,2,null,3,null,3] is not:
1
/ \
2 2
\ \
3 3
public boolean isSymmetric(TreeNode root) {
return root == null || checkSymmetric(root.left, root.right);
}
// Deep-First Search (Pre-Order Traversal)
private boolean checkSymmetric(TreeNode left, TreeNode right) {
if (left == null && right == null)
return true;
if (left != null && right != null) {
return left.val == right.val && checkSymmetric(left.left, right.right) && checkSymmetric(left.right, right.left);
}
return false;
}
// Bread-First Search
public boolean isSymmetric2(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
if (root == null)
return true;
queue.add(root.left);
queue.add(root.right);
while (queue.size() > 1) {
TreeNode left = queue.poll(), right = queue.poll();
if (left == null && right == null)
continue;
if (left == null || right == null)
return false;
if (left.val != right.val)
return false;
queue.add(left.left);
queue.add(right.right);
queue.add(left.right);
queue.add(right.left);
}
return true;
}
Binary Tree 0/1
There is a complete binary tree with just value 0 or 1, the left child value is the same as parent value, the right child is NOT. Given a node which is on n level and k index, return the value of it.
0 (1,1)
/ \
0 1 (2,1; 2,2)
/ \ / \
0 1 1 0 (3,1; 3,2; 3,3; 3,4)
// bottom-up recursion, trace all the way up to root
public static int findNodeValue(int n, int k) {
if (n == 1)
return k - 1; // root's value
int parent = findNodeValue(n - 1, (k + 1) / 2);
if (k % 2 != 0) {
return parent;
} else {
return parent == 0 ? 1 : 0;
}
}
Lowest Common Ancestor
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself).”
// Deep-First Search (Post-Order Traversal)
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// if (root == null || root == p || root == q) // two given nodes in the tree
if (root == null || root.val == p.val || root.val == q.val)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null)
return root;
else
return left == null ? right : left;
}
LCA with A Parent Pointer
Given two nodes in a binary tree, design an algorithm that computes their LCA. Assume that each node has a parent pointer.
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/
// If the nodes are at the same depth, we can move up the tree in tandem from both nodes,
// stopping at the first common node, which is the LCA.
public Node lowestCommonAncestor(Node node0, Node node1) {
int depth0 = getDepth(node0);
int depth1 = getDepth(node1);
// Make sure node0 as the deeper node to simplify the code.
if (depth1 > depth0) {
Node temp = node0;
node0 = node1;
node1 = temp;
}
// Ascends from the deeper node
int depthDiff = Math.abs(depth0 - depth1);
while (depthDiff > 0) {
node0 = node0.parent;
depthDiff--;
}
// Now ascend both nodes until we reach the LCA
while (node0 != node1) {
node0 = node0.parent;
node1 = node1.parent;
}
return node0;
}
private int getDepth(Node node) {
int depth = 0;
while (node.parent != null) {
depth++;
node = node.parent;
}
return depth;
}
// We can also alternately moving upwards from the two nodes and storing the nodes visited in a
// hash table. Each time we visited a node we check to see if it has been visited before._
public Node lowestCommonAncestor2(Node node0, Node node1) {
Set<Node> visited = new HashSet<>();
while (node0 != null || node1 != null) {
if (node0 != null) {
if (!visited.add(node0))
return node0;
node0 = node0.parent;
}
if (node1 != null) {
if (!visited.add(node1))
return node1;
node1 = node1.parent;
}
}
throw new IllegalArgumentException("node0 and node1 are not in the same tree");
}
// Simply move upwards with null checking and switch over
public Node lowestCommonAncestor3(Node p, Node q) {
Node a = p, b = q;
while (a != b) {
a = a == null ? q : a.parent;
b = b == null ? p : b.parent;
}
return a;
}
Sum Root to Leaf Numbers
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
For example,
1
/ \
2 3
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Return the sum = 12 + 13 = 25.
public int sumRootToLeaf(TreeNode root) {
return sumRootToLeaf(root, 0);
}
private int sumRootToLeaf(TreeNode node, int pathSum) {
if (node == null)
return 0;
pathSum = pathSum * 10 + node.val; // pathSum * 2 to handle binary digits
if (node.left == null && node.right == null)
return pathSum;
return sumRootToLeaf(node.left, pathSum) + sumRootToLeaf(node.right, pathSum);
}
Pre-Order Iterative Traversal
public List<Integer> preorderTraverse(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
if (root != null) {
stack.push(root);
}
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val); // add before going to children
if (node.right != null)
stack.push(node.right);
if (node.left != null)
stack.push(node.left);
}
return result;
}
In-Order Iterative Traversal
public List<Integer> inorderTraverse(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
if (node != null) {
stack.push(node);
node = node.left;
} else {
node = stack.pop();
result.add(node.val); // add after all left children
node = node.right;
}
}
return result;
}
Post-Order Iterative Traversal
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> result = new LinkedList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode p = root;
while (!stack.isEmpty() || p != null) {
if (p != null) {
stack.push(p);
result.addFirst(p.val); // Reverse the process of preorder
p = p.right; // Reverse the process of preorder
} else {
TreeNode node = stack.pop();
p = node.left; // Reverse the process of preorder
}
}
return result;
}
In-Order Traverse with Parents
Write a non-recursive program for computing the in-order traversal sequence for a binary tree. Assume nodes have parent fields.
Idea: To complete this algorithm, we need to know when we return to a parent if the just completed subtree was the parent’s left child (in which case we need to visit the parent and then traverse its right subtree) or a right subtree (in which case we have completed traversing the parent).
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
TreeNode prev = null, curr = root;
while (curr != null) {
TreeNode next = null;
if (curr.parent == prev) {
// we came down to curr from prev
if (curr.left != null)
next = curr.left;
else {
result.add(curr.val);
// done with left, go right or go up
next = curr.right != null ? curr.right : curr.parent;
}
} else if (curr.left == prev) {
result.add(curr.val);
next = curr.right != null ? curr.right : curr.parent;
} else {
// done with both children , so move up.
next = curr.parent;
}
prev = curr;
curr = next;
}
return result;
}
Level Order Traversal of a Binary Tree
Similar question like: Find Largest Value in Each Tree Row
Given a binary tree, return the level order traversal of its node values. (ie, from left to right, level by level).
For example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its level order traversal as:
[
[3],
[9,20],
[15,7]
]
We can use a queue of nodes to store nodes at depth i. When processing all nodes at depth i, also put the depth i + 1 nodes in the queue. Also we can use Deep-First Search to simplify the code
// BFS
public class BinaryTreeLevelOrderTraversal {
public List<List<Integer>> levelOrderWithIteration(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> result = new LinkedList<>();
if (root == null)
return result;
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> list = new LinkedList<>();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
}
result.add(0, list);
}
return result;
}
// DFS
public List<List<Integer>> levelOrderWithRecursion(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
deepFirstSearch(result, root, 0);
return result;
}
private void deepFirstSearch(List<List<Integer>> result, TreeNode root, int depth) {
if (root == null)
return;
if (depth >= result.size())
result.add(new ArrayList<Integer>());
result.get(depth).add(root.val);
deepFirstSearch(result, root.left, depth + 1);
deepFirstSearch(result, root.right, depth + 1);
}
}
Vertical Order Traversal of a Binary Tree
Given the root of a binary tree, calculate the vertical order traversal of the binary tree.
For each node at position (row, col), its left and right children will be at positions (row + 1, col - 1) and (row + 1, col + 1) respectively. The root of the tree is at (0, 0).
The vertical order traversal of a binary tree is a list of top-to-bottom orderings for each column index starting from the leftmost column and ending on the rightmost column. There may be multiple nodes in the same row and same column. In such a case, sort these nodes by their values.
Return the vertical order traversal of the binary tree.
For example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its vertical order traversal as:
[
[9],
[3,15],
[20],
[7]
]
/**
* Solution: Use BFS/DFS with Partition Sorting
* Time Complexity: O(Nlog(N/k)), k is the width/columns of the tree.
*/
public class VerticalOrderTraversal {
int minCol = 0, maxCol = 0;
Map<Integer, List<int[]>> colMap = new HashMap<>();
private void dfsTraverse(TreeNode node, int row, int col) {
if (node == null)
return;
minCol = Math.min(minCol, col);
maxCol = Math.max(maxCol, col);
// preorder/inorder/postorder all work here!
dfsTraverse(node.left, row + 1, col - 1);
colMap.computeIfAbsent(col, key -> new ArrayList<>()).add(new int[] { row, node.val });
dfsTraverse(node.right, row + 1, col + 1);
}
public List<List<Integer>> verticalTraversal(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
dfsTraverse(root, 0, 0);
for (int i = minCol; i <= maxCol; i++) {
Collections.sort(colMap.get(i), (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
List<Integer> values = new ArrayList<>();
colMap.get(i).forEach(a -> values.add(a[1]));
result.add(values);
}
return result;
}
}
Flatten Binary Tree to Linked List
Given a binary tree, flatten it to a linked list in-place.
For example, given the following tree:
1
/ \
2 5
/ \ \
3 4 6
The flattened tree should look like:
1
\
2
\
3
\
4
\
5
\
6
public void flattenBinaryTree(TreeNode root) {
if (root == null)
return;
TreeNode left = root.left;
TreeNode right = root.right;
root.left = null;
flattenBinaryTree(left);
flattenBinaryTree(right);
root.right = left;
TreeNode cur = root;
// all the way to max left!
while (cur.right != null)
cur = cur.right;
cur.right = right;
}
Second Minimum In a Binary Tree
Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes.
Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.
If no such second minimum value exists, output -1 instead.
Example 1:
Input:
2
/ \
2 5
/ \
5 7
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.
Use a brute-force or ad-hoc checking.
int min1;
long ans = Long.MAX_VALUE;
public void dfs(TreeNode root) {
if (root != null) {
if (min1 < root.val && root.val < ans) {
ans = root.val;
} else if (min1 == root.val) {
dfs(root.left);
dfs(root.right);
}
}
}
public int findSecondMinimumValue(TreeNode root) {
min1 = root.val;
dfs(root);
return ans < Long.MAX_VALUE ? (int) ans : -1;
}
Create A List Of Leaves
Given a binary tree, compute a linked list from the leaves of the binary tree.
public List<TreeNode> createListOfLeaves(TreeNode root) {
List<TreeNode> leaves = new ArrayList<>();
addLeavesLeftToRight(root, leaves);
return leaves;
}
public void addLeavesLeftToRight(TreeNode node, List<TreeNode> leaves) {
if (node == null)
return;
if (node.left == null && node.right == null)
leaves.add(node);
else {
addLeavesLeftToRight(node.left, leaves);
addLeavesLeftToRight(node.right, leaves);
}
}
Find Leaves of Binary Tree
Given a binary tree, collect a tree’s nodes as if you were doing this: Collect and remove all leaves, repeat until the tree is empty.
Example:
Input: [1,2,3,4,5]
1
/ \
2 3
/ \
4 5
Output: [[4,5,3],[2],[1]]
public List<List<Integer>> findLeaves(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
height(root, res);
return res;
}
private int height(TreeNode node, List<List<Integer>> res) {
if (null == node)
return -1;
int level = 1 + Math.max(height(node.left, res), height(node.right, res));
if (res.size() < level + 1)
res.add(new ArrayList<>());
res.get(level).add(node.val);
return level;
}
Binary Tree Right Side View
Given a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example:
Input: [1,2,3,null,5,null,4]
Output: [1, 3, 4]
Explanation:
1 <---
/ \
2 3 <---
\ \
5 4 <---
Solution #1: Use DFS with two stacks.
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int maxDepth = -1;
/* These two stacks are always synchronized, providing an implicit
* association values with the same offset on each stack. */
Stack<TreeNode> nodeStack = new Stack<TreeNode>();
Stack<Integer> depthStack = new Stack<Integer>();
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
maxDepth = Math.max(maxDepth, depth);
/* The first node that we encounter at a particular depth contains
* the correct value. */
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
/* Construct the solution based on the values that we end up with at the end. */
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= maxDepth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
Solution #2: Use DFS with recursion
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null)
return res;
dfs(root, res, 0);
return res;
}
public void dfs(TreeNode root, List<Integer> res, int level) {
if (root == null)
return;
if (res.size() == level)
res.add(root.val);
// To get left side view, just need to swap these 2 line!
dfs(root.right, res, level + 1);
dfs(root.left, res, level + 1);
}
Find Exterior Of Binary Tree
Write a program that computes the exterior of a binary tree.
We can compute the nodes on the path from the root to the leftmost leaf and the leaves in the left subtree in one traversal. After that, we find the leaves in the right subtree followed by the nodes from the rightmost leaf to the root with another traversal. Please note the bottom leaves will be included as well.
public List<TreeNode> findExteriorOfBinaryTree(TreeNode root) {
List<TreeNode> exterior = new LinkedList<>();
if (root != null) {
exterior.add(root);
exterior.addAll(leftBoundaryAndLeaves(root.left, true));
exterior.addAll(rightBoundaryAndLeaves(root.right, true));
}
return exterior;
}
// Top-Down
private List<TreeNode> leftBoundaryAndLeaves(TreeNode node, boolean isBoundary) {
List<TreeNode> result = new LinkedList<>();
if (node != null) {
if (isBoundary || isLeaf(node))
result.add(node);
result.addAll(leftBoundaryAndLeaves(node.left, isBoundary));
result.addAll(leftBoundaryAndLeaves(node.right, isBoundary && node.left == null));
}
return result;
}
// Bottom-Up
private List<TreeNode> rightBoundaryAndLeaves(TreeNode node, boolean isBoundary) {
List<TreeNode> result = new LinkedList<>();
if (node != null) {
result.addAll(rightBoundaryAndLeaves(node.left, isBoundary && node.right == null));
result.addAll(rightBoundaryAndLeaves(node.right, isBoundary));
if (isBoundary || isLeaf(node))
result.add(node);
}
return result;
}
private boolean isLeaf(TreeNode node) {
return node.left == null && node.right == null;
}
Construct Right Siblings
Write a program that takes a perfect binary tree, and set each node’s level-next field to the node on its right, if one exists.
For example,
Given the following perfect binary tree,
1
/ \
2 3
/ \ / \
4 5 6 7
After calling your function, the tree should look like:
1 -> NULL
/ \
2 -> 3 -> NULL
/ \ / \
4->5->6->7 -> NULL
public void constructRightSibling(TreeNode node) {
TreeNode leftStart = node;
while (leftStart != null && leftStart.left != null) {
populateLowerLevelNextField(leftStart);
leftStart = leftStart.left;
}
}
private void populateLowerLevelNextField(TreeNode startNode) {
TreeNode node = startNode;
while (node != null) {
node.left.next = node.right;
if (node.next != null) {
node.right.next = node.next.left;
}
node = node.next;
}
}
Serialize and Deserialize
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Example:
You may serialize the following tree:
1
/ \
2 3
/ \
4 5
as "[1,2,3,null,null,4,5]"
public class Codec {
private static final String spliter = ",";
private static final String NN = "X";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
buildString(root, sb);
return sb.toString();
}
private void buildString(TreeNode node, StringBuilder sb) {
if (node == null) {
sb.append(NN).append(spliter);
} else {
sb.append(node.val).append(spliter);
buildString(node.left, sb);
buildString(node.right, sb);
}
}
public TreeNode deserialize(String data) {
Deque<String> nodes = new LinkedList<>();
nodes.addAll(Arrays.asList(data.split(spliter)));
return buildTree(nodes);
}
private TreeNode buildTree(Deque<String> nodes) {
String val = nodes.remove();
if (val.equals(NN))
return null;
else {
TreeNode node = new TreeNode(Integer.valueOf(val));
node.left = buildTree(nodes);
node.right = buildTree(nodes);
return node;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
}
Path Sum II
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where each path’s sum equals targetSum.
Time Complexity: O(N^2), In the worst case, we could have a complete binary tree and if that is the case, then there would be N/2 leafs. For every leaf, we perform a potential O(N) operation of copying over the pathNodes nodes to a new list to be added to the final pathsList. Hence, the complexity in the worst case could be O(N^2).
Space Complexity: O(N) or O(N^2) if count in the space occupied by the output.
public List<List<Integer>> pathSumII(TreeNode root, int sum) {
List<List<Integer>> results = new ArrayList<>();
recurseTree(results, new ArrayList<>(), root, sum);
return results;
}
private void recurseTree(List<List<Integer>> results, List<Integer> path, TreeNode node, int remain) {
if (node == null) {
return;
}
path.add(node.val);
if (node.val == remain && node.left == null && node.right == null) {
results.add(new ArrayList<>(path));
} else {
recurseTree(results, path, node.left, remain - node.val);
recurseTree(results, path, node.right, remain - node.val);
}
path.remove(path.size() - 1);
}
Path Sum III
Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
Solution:
Parse the tree using recursive preorder traversal, also use prefix sum technique along the way to “Find a number of continuous subarrays/submatrices/tree paths that sum to target.”
Complexity Analysis:
Time complexity: O(N), where N N is a number of nodes. During preorder traversal, each node is visited once.
Space complexity: up to O(N) to keep the hash map of prefix sums, where N is a number of nodes.
public int pathSumIII(TreeNode root, int target) {
AtomicInteger count = new AtomicInteger(0);
Map<Integer, Integer> sumMap = new HashMap<>();
recurseTree(root, count, sumMap, 0, target);
return count.get();
}
private void recurseTree(TreeNode node, AtomicInteger count, Map<Integer, Integer> sumMap, int prefixSum, int targetSum) {
if (node == null) {
return;
}
// Current prefix sum
prefixSum += node.val;
// Continous subarray starts from the beggining of the array
if (prefixSum == targetSum) {
count.addAndGet(1);
}
// Number of times the current - target has occured already.
count.addAndGet(sumMap.getOrDefault(prefixSum - targetSum, 0));
sumMap.put(prefixSum, sumMap.getOrDefault(prefixSum, 0) + 1);
recurseTree(node.left, count, sumMap, prefixSum, targetSum);
recurseTree(node.right, count, sumMap, prefixSum, targetSum);
sumMap.put(prefixSum, sumMap.get(prefixSum) - 1);
}
Heaps
What is Heap?
- A max-heap is specialized binary tree. The key at each node is at least as great as the keys stored at its children.
- A max-heap can be implemented as an array, the children of the node at position n would be at positions 2n and 2n + 1 in a one-based array, or 2n + 1 and 2n + 2 in a zero-based array. It’s parent is found at index (n - 1) / 2 in a zero-based array.
- A max-heap supports O(log(n)) insertions, O(1) time lookup for the max element, and O(log(n)) deletion of the max elements. Searching for arbitrary keys has O(n) time complexity.
- Deletion is performed by replacing the root’s key with the key at the last leaf and then recovering the heap property by repeatedly exchanging keys with children.
- Use a heap when all you care about is the K largest or smallest elements, and you do not need to support fast lookup, delete, or search operations for arbitrary elements.
- A heap is sometimes referred to as a priority queue.
Heaps Boot Camp
Merge A List Of Sorted Arrays
Write a program that takes as input a set of sorted sequences and computes the union of these sequences as a sorted sequence. For example, if the input is [3, 5, 7], [0, 6], and [0, 6, 28], then the output is [0, 0, 3, 5, 6, 6, 7, 28].
There are no more than k elements in the min-heap. Both extract-min and insert take O(log(k)) time. Hence, we can do the merge in O(nlog(k)) time.
public static List<Integer> mergeSortedArrays(List<List<Integer>> sortedArrays) {
List<Iterator<Integer>> iters = new ArrayList<>();
for (List<Integer> array : sortedArrays) {
iters.add(array.iterator());
}
Queue<int[]> minHeap = new PriorityQueue<>(sortedArrays.size(), (a, b) -> (a[0] - b[0]));
for (int i = 0; i < iters.size(); i++) {
if (iters.get(i).hasNext())
minHeap.offer(new int[] { iters.get(i).next(), i });
}
List<Integer> result = new ArrayList<>();
while (!minHeap.isEmpty()) {
int[] element = minHeap.poll();
result.add(element[0]);
if (iters.get(element[1]).hasNext())
minHeap.offer(new int[] { iters.get(element[1]).next(), element[1] });
}
return result;
}
Sort An Increasing-Decreasing Array
An array is said to be k-increasing-decreasing if elements repeatedly increase up to a certain index after which they decrease, then again increase, a total of k times. The solution is to decompose this list to a list of sorted sub arrays, and merge them!
public static List<Integer> sortKIncreasingDecreasingArray(List<Integer> A) {
List<List<Integer>> sortedSubarrays = new ArrayList<>();
boolean isIncreasing = true;
int startIdx = 0;
for (int i = 1; i <= A.size(); i++) {
if (i == A.size() || (A.get(i - 1) < A.get(i) && !isIncreasing)
|| (A.get(i - 1) >= A.get(i) && isIncreasing)) {
List<Integer> subList = A.subList(startIdx, i);
if (!isIncreasing)
Collections.reverse(subList);
sortedSubarrays.add(subList);
startIdx = i;
isIncreasing = !isIncreasing;
}
}
return mergeSortedArrays(sortedSubarrays);
}
Sort An Almost Sorted Array
Take as input a very long sequence of numbers and prints the numbers in sorted order. Each number is at most k away from its correctly sorted position. For example, no number in the sequence (3, -1, 2, 6, 4, 5, 8) is more than 2 away from its final sorted position.
Idea: after we have read k+1 numbers, the smallest number in that group must be smaller than all following numbers.
public static List<Integer> sortAnAmostSortedData(Iterator<Integer> sequence, int k) {
List<Integer> result = new ArrayList<>();
Queue<Integer> minHeap = new PriorityQueue<>(k + 1);
for (int i = 0; i < k && sequence.hasNext(); i++) {
minHeap.offer(sequence.next());
}
while (!minHeap.isEmpty()) {
if (sequence.hasNext())
minHeap.offer(sequence.next());
result.add(minHeap.poll());
}
return result;
}
Compute Online Median
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Examples: [2, 3, 4] , the median is 3; [1, 2, 3, 9], the median is (2 + 3) / 2 = 2.5.
public static List<Double> computeOnlineMedian(Iterator<Integer> sequence) {
Queue<Integer> minHeap = new PriorityQueue<>();
Queue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());
List<Double> result = new ArrayList<>();
while (sequence.hasNext()) {
// make sure the number was sorted in both heaps
minHeap.add(sequence.next());
maxHeap.add(minHeap.poll());
// equal number of elements, or minHeap must have one more!
if (maxHeap.size() > minHeap.size())
minHeap.add(maxHeap.poll());
result.add(minHeap.size() == maxHeap.size() ? 0.5 * (minHeap.peek() + maxHeap.peek())
: (double) minHeap.peek());
}
return result;
}
Median of Two Sorted Arrays
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
You may assume nums1 and nums2 cannot be both empty.
Solution:
They are sorted arrays, apply the binary search with O(log(min(m,n))).
- i+j=m−i+n−j (or: m−i+n−j+1), if n≥m, we just need to set: i=0∼m, j=(m+n+1)/2−i
- B[j−1]≤A[i] and A[i−1]≤B[j]
public double findMedianSortedArrays(int[] A, int[] B) {
if (A.length > B.length) { // use the small one for binary search
int[] temp = A;
A = B;
B = temp;
}
// prone to use left for odd numbers
int left = 0, right = A.length, halfLen = (A.length + B.length + 1) / 2;
while (left <= right) {
int i = (left + right) / 2;
int j = halfLen - i;
if (i < right && B[j - 1] > A[i]) {
left = i + 1; // i is too small
} else if (i > left && A[i - 1] > B[j]) {
right = i - 1; // i is too big
} else { // i is perfect
int maxLeft = 0;
if (i == 0) {
maxLeft = B[j - 1];
} else if (j == 0) {
maxLeft = A[i - 1];
} else {
maxLeft = Math.max(A[i - 1], B[j - 1]);
}
if ((A.length + B.length) % 2 == 1) {
return maxLeft;
}
int minRight = 0;
if (i == A.length) {
minRight = B[j];
} else if (j == B.length) {
minRight = A[i];
} else {
minRight = Math.min(B[j], A[i]);
}
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
Compute K Largest Elements
Given a max-heap, represented as an array A, design an algorithm that computes the k largest elements sorted in the max-heap. You can not modify the heap.
A parent node always stores value greater than or equal to the values stored at its children (2k + 1 or 2k + 2).
public static List<Integer> computeKLargestInBinaryHeap(List<Integer> A, int k) {
List<Integer> result = new ArrayList<>();
if (k <= 0)
return result;
// int[] -> index, value
Queue<int[]> candidateMaxHeap = new PriorityQueue<>((a, b) -> (b[1] - a[1]));
candidateMaxHeap.offer(new int[] { 0, A.get(0) });
for (int i = 0; i < k; i++) {
Integer candidateIdx = candidateMaxHeap.peek()[0];
result.add(candidateMaxHeap.poll()[1]);
int leftChildIdx = 2 * candidateIdx + 1;
if (leftChildIdx < A.size())
candidateMaxHeap.offer(new int[] { leftChildIdx, A.get(leftChildIdx) });
int rightChildIdx = 2 * candidateIdx + 2;
if (rightChildIdx < A.size())
candidateMaxHeap.offer(new int[] { rightChildIdx, A.get(rightChildIdx) });
}
return result;
}
Design Priority Queue
Many applications require that we process items having keys in order, but not necessarily in full sorted order and not necessarily all at once. Often, we collect a set of items, then process the one with the largest key, then perhaps collect more items, then process the one with the current largest key, and so forth. An appropriate data type in such an environment supports two operations: remove the maximum and insert. Such a data type is called a priority queue.
A priority queue is an abstract data type which is like a regular queue or stack data structure, but where additionally each element has a “priority” associated with it. In a priority queue, an element with high priority is served before an element with low priority. If two elements have the same priority, they are served according to their order in the queue. Here priority queue is implemented using a max heap.
A binary heap is a set of nodes with keys arranged in a complete heap-ordered binary tree, represented in level order in an array (not using the first entry). In a heap, the parent of the node in position k is in position k/2; and, conversely, the two children of the node in position k are in positions 2k and 2k + 1. We can travel up and down by doing simple arithmetic on array indices: to move up the tree from a[k] we set k to k/2; to move down the tree we set k to 2k or 2k+1.
public class PriorityQueue {
private Task[] heap;
private int heapSize, capacity;
public PriorityQueue(int capacity) {
this.capacity = capacity + 1; // not using the first entry, starts with 1
heap = new Task[this.capacity];
heapSize = 0;
}
public void clear() {
heap = new Task[capacity];
heapSize = 0;
}
public boolean isEmpty() {
return heapSize == 0;
}
public boolean isFull() {
return heapSize == capacity - 1;
}
public int size() {
return heapSize;
}
// Bottom-up reheapify (swim).
public void insert(String job, int priority) {
if (isFull()) {
System.out.println("Heap is full!");
return;
}
Task newJob = new Task(job, priority);
// insert to the bottom and swim up!
heap[++heapSize] = newJob;
int pos = heapSize;
while (pos > 1 && newJob.priority > heap[pos / 2].priority) {
heap[pos] = heap[pos / 2];
pos /= 2;
}
heap[pos] = newJob;
}
// Top-down heapify (sink).
// Remove the max, exchange task with root, and sink down
public Task remove() {
if (isEmpty()) {
System.out.println("Heap is empty!");
return null;
}
Task item = heap[1];
// assign head to the last item and sink down
heap[1] = heap[heapSize--];
// Task temp = heap[heapSize--];
int parent = 1;
while (parent <= heapSize / 2) { // half
int child = parent << 1;
if (child < heapSize && heap[child].priority < heap[child + 1].priority)
child++;
if (heap[parent].priority >= heap[child].priority)
break;
heap[parent] = heap[child];
parent = child;
}
return item;
}
class Task {
String job;
int priority;
public Task(String job, int priority) {
this.job = job;
this.priority = priority;
}
public String toString() {
return "Job: " + job + "; priority: " + priority;
}
}
public static void main(String[] args) {
PriorityQueue queue = new PriorityQueue(3);
queue.insert("first", 1);
queue.insert("second", 5);
queue.insert("third", 3);
System.out.println(queue.remove());
queue.insert("fourth", 4);
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
}
}
Binary Search Trees
-
Binary Search Trees (BSTs) have the key stored at a node is greater than or equal to the keys stored at the nodes of its left subtree and less than or equal to the keys stored in the nodes of its right subtree.
-
BST offers the ability to find the min and max elements, and find the next largest/next smallest element with O(lgn) complexity. To check if a given value is present in a BST, it just spends O(1) time per level, the time complexity is O(h) or O(1.39lgn), where h is the height of the tree.
-
Balanced Search Trees (2-3 Search Trees, Red-black BSTs and AVL BSTs) can provide consistent average O(1.00lgn) cost on search and insertion.
-
In Java, TreeSet and TreeMap are two BST-based data structures. When a mutable object in a BST is to be updated, always first remove it from the tree, then update it, then add it back!
BST Basic Operations
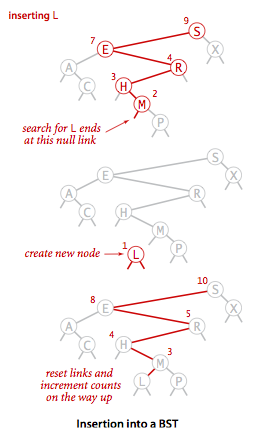 |
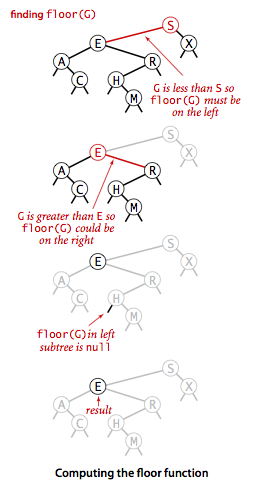 |
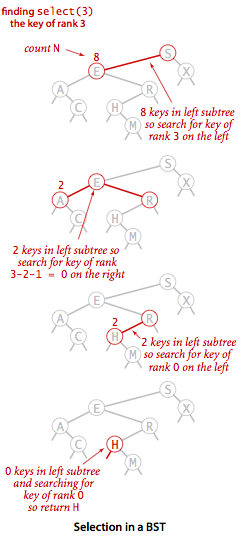 |
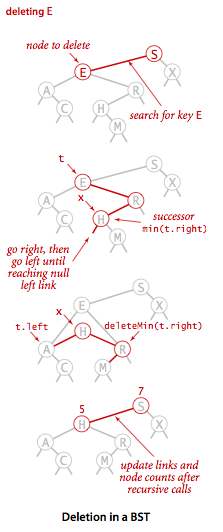 |
private Node put(Node x, Key key, Value val) {
if (x == null)
return new Node(key, val, 1);
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = put(x.left, key, val);
else if (cmp > 0)
x.right = put(x.right, key, val);
else
x.val = val;
// update the node size up to root
x.size = 1 + size(x.left) + size(x.right);
return x;
}
private Node floor(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return floor(x.left, key);
Node t = floor(x.right, key);
if (t != null)
return t;
else
return x;
}
// Return key of rank k.
private Node select(Node x, int k) {
if (x == null)
return null;
int t = size(x.left);
if (t > k)
return select(x.left, k);
else if (t < k)
return select(x.right, k - t - 1);
else
return x;
}
private Node min(Node x) {
if (x.left == null)
return x;
else
return min(x.left);
}
private Node deleteMin(Node x) {
if (x.left == null)
return x.right;
x.left = deleteMin(x.left);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
private Node delete(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = delete(x.left, key);
else if (cmp > 0)
x.right = delete(x.right, key);
else {
if (x.right == null)
return x.left; // easy to handle just left side
if (x.left == null)
return x.right; // easy to handle just right side
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
// update node counts after recursive call
x.size = size(x.left) + size(x.right) + 1;
return x;
}
// return the keys in a given range. (inorder traversal)
private void keys(Node x, List<Key> queue, Key lo, Key hi) {
if (x == null)
return;
int cmplo = lo.compareTo(x.key);
int cmphi = hi.compareTo(x.key);
if (cmplo < 0)
keys(x.left, queue, lo, hi);
if (cmplo <= 0 && cmphi >= 0)
queue.add(x.key);
if (cmphi > 0)
keys(x.right, queue, lo, hi);
}
Balanced Search Trees
- A 2-3 search tree is a tree that is either empty or
- A 2-node, with one key (and associated value) and two links, a left link to a 2-3 search tree with smaller keys, and a right link to a 2-3 search tree with larger keys.
- A 3-node, with two keys (and associated values) and three links, a left link to a 2-3 search tree with smaller keys, a middle link to a 2-3 search tree with keys between the node’s keys, and a right link to a 2-3 search tree with larger keys.
- Unlike standard BSTs, which grow down from the top, 2-3 trees grow up from the bottom. The search and insert operations in a 2-3 tree with n keys are guaranteed to visit a most lgn + 1 nodes.
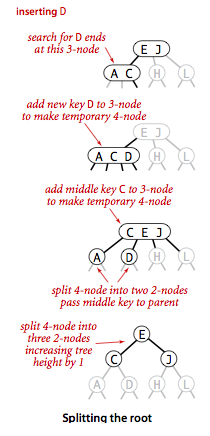
- The Red-Black BST is to encode 2-3 trees by starting with standard BST (which are made up of 2-nodes) and adding extra information to encode 3-nodes. We think of the links as being of two different types: red links, which bind together two 2-nodes to represent 3-nodes, and black links, which bind together the 2-3 tree.
- Red links lean left.
- No node has two red links connected to it.
- The tree has perfect black balance.
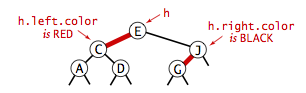
- The AVL BST relies on an extra attribute balance factor on each node to indicate whether the tree is left-heavy, balanced or right-heavy. If the balance would be destroyed by an insertion, a rotation is performed to correct the balance.
Red-Black BST Insertion
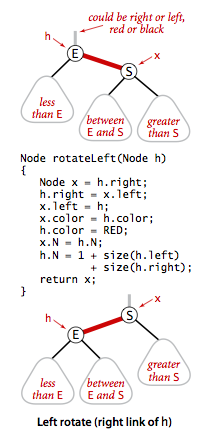 |
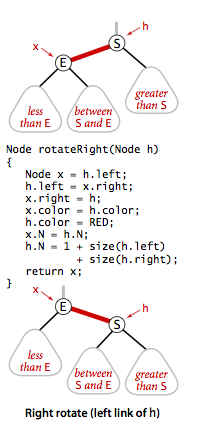 |
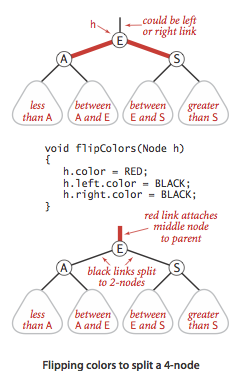 |
public class RedBlackBST<Key extends Comparable<Key>, Value> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private Node root; // root of the BST
private class Node {
private Key key;
private Value val;
private Node left, right;
private boolean color;
private int size;
public Node(Key key, Value val, boolean color, int size) {
this.key = key;
this.val = val;
this.color = color;
this.size = size;
}
}
public RedBlackBST() {
}
private boolean isRed(Node node) {
return node == null ? false : node.color == RED;
}
private int size(Node node) {
return node == null ? 0 : node.size;
}
public int size() {
return size(root);
}
public boolean isEmpty() {
return root == null;
}
/* Standard BST search */
public Value get(Key key) {
if (key == null)
throw new IllegalArgumentException();
return get(root, key);
}
private Value get(Node node, Key key) {
while (node != null) {
int cmp = key.compareTo(node.key);
if (cmp < 0)
node = node.left;
else if (cmp > 0)
node = node.right;
else
return node.val;
}
return null;
}
public boolean contains(Key key) {
return get(key) != null;
}
/* Red-blank tree insertion */
public void put(Key key, Value val) {
if (key == null)
throw new IllegalArgumentException();
if (val == null) {
// delete(key);
return;
}
root = put(root, key, val);
root.color = BLACK;
}
private Node put(Node node, Key key, Value val) {
if (node == null)
return new Node(key, val, RED, 1);
int cmp = key.compareTo(node.key);
if (cmp < 0)
node.left = put(node.left, key, val);
else if (cmp > 0)
node.right = put(node.right, key, val);
else
node.val = val;
// fix-up any right-leaning links
if (isRed(node.right) && !isRed(node.left))
node = rotateLeft(node);
if (isRed(node.left) && isRed(node.left.left))
node = rotateRight(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
node.size = size(node.left) + size(node.right) + 1;
return node;
}
private Node rotateLeft(Node node) {
Node temp = node.right;
node.right = temp.left;
temp.left = node;
temp.color = temp.left.color;
temp.left.color = RED;
temp.size = node.size;
node.size = size(node.left) + size(node.right) + 1;
return temp;
}
private Node rotateRight(Node node) {
Node temp = node.left;
node.left = temp.right;
temp.right = node;
temp.color = temp.right.color;
temp.right.color = RED;
temp.size = node.size;
node.size = size(node.left) + size(node.right) + 1;
return temp;
}
private void flipColors(Node node) {
node.color = !node.color;
node.left.color = !node.left.color;
node.right.color = !node.right.color;
}
}
B-Trees Anatomy
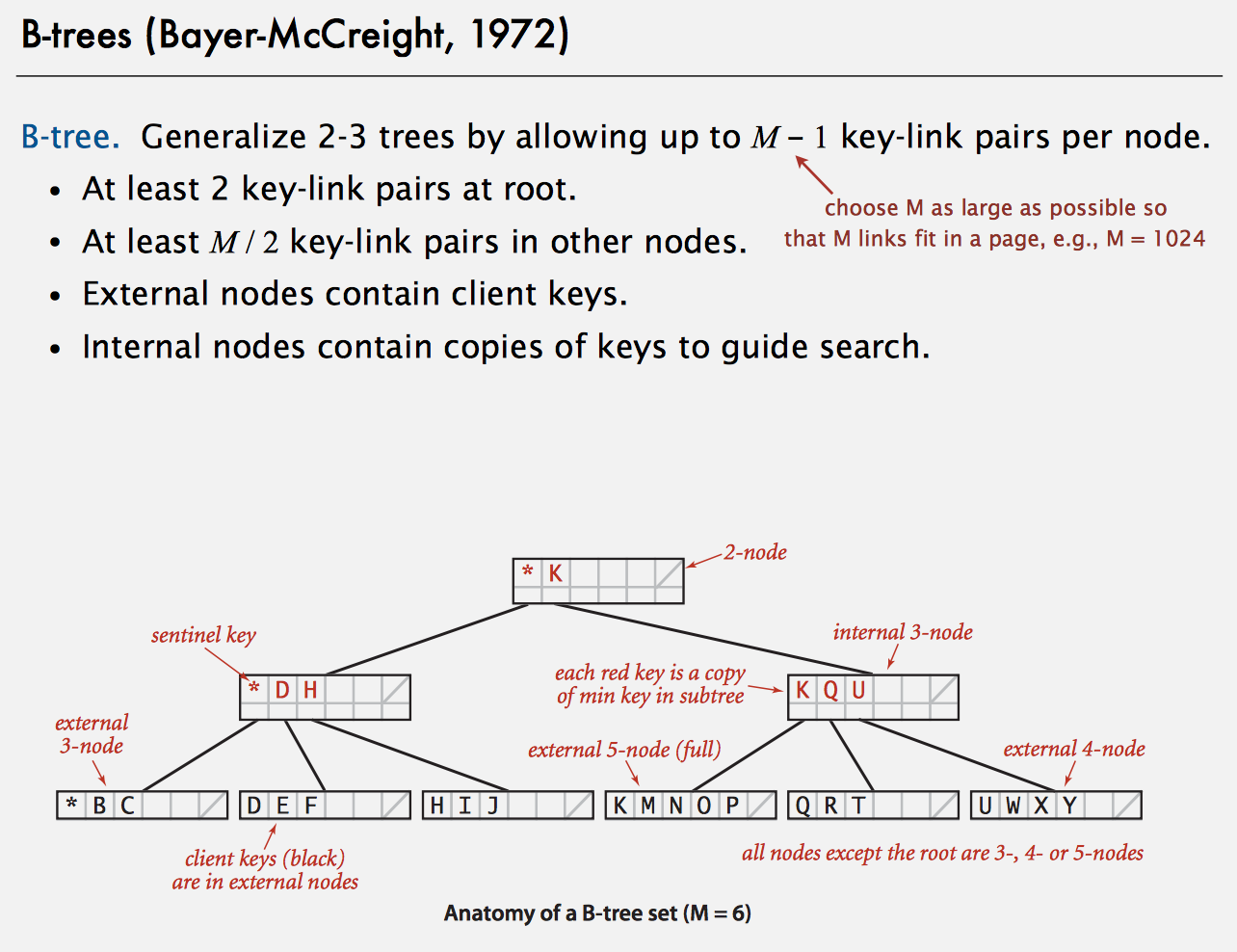
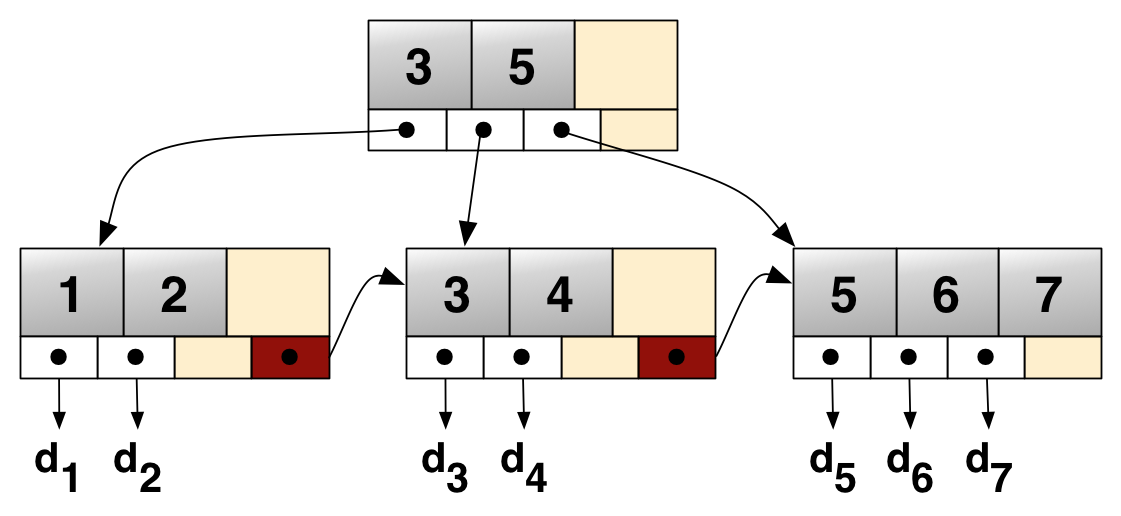
-
In B-Trees, internal (non-leaf) nodes can have a variable number of child nodes within some pre-defined range. When data is inserted or removed from a node, its number of child nodes changes.
-
A B+ tree can be viewed as a B-tree in which each node contains only keys (not key–value pairs), and to which an additional level is added at the bottom with linked leaves.
-
The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context — in particular, filesystems. This is primarily because unlike binary search trees, B+ trees have very high fanout (number of pointers to child nodes in a node, typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree.
-
A search or an insertion in a B-tree of order M with N keys requires between \(\log_{M-1}N\) and \(\log_{M/2}N\) probes. All internal nodes (besides root) have between M/2 and M-1 links.
-
In Practice, number of probes is at most 4. M = 1024; N = 62 billion; \(\log_{M/2}N <= 4\). And always keep root page in memory.
-
Red-black trees are widely used as system symbol tables: Java TreeMap, TreeSet. B-trees are widely used for file systems and databases: NTFS, HFS, JFS, Oracle, PostgreSQL.
public class BTree<Key extends Comparable<Key>, Value> {
// max children per B-tree node = M-1
// (must be even and greater than 2)
private static final int M = 4;
private Node root; // root of the B-tree
private int height; // height of the B-tree
private int n; // number of key-value pairs in the B-tree
// helper B-tree node data type
private static final class Node {
private int m; // number of children
private Entry[] children = new Entry[M]; // the array of children
// create a node with k children
private Node(int k) {
m = k;
}
}
// internal nodes: only use key and next
// external nodes: only use key and value
private static class Entry {
private Comparable<?> key;
private final Object val;
private Node next; // helper field to iterate over array entries
public Entry(Comparable<?> key, Object val, Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
public BTree() {
root = new Node(0);
}
public boolean isEmpty() {
return size() == 0;
}
public int size() {
return n;
}
public int height() {
return height;
}
public Value get(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to get() is null");
return search(root, key, height);
}
private Value search(Node x, Key key, int ht) {
Entry[] children = x.children;
// external node
if (ht == 0) {
for (int j = 0; j < x.m; j++) {
if (eq(key, children[j].key))
return (Value) children[j].val;
}
}
// internal node
else {
for (int j = 0; j < x.m; j++) {
if (j + 1 == x.m || less(key, children[j + 1].key))
return search(children[j].next, key, ht - 1);
}
}
return null;
}
/**
* Inserts the key-value pair into the symbol table, overwriting the old value with the new
* value if the key is already in the symbol table. If the value is {@code null}, this
* effectively deletes the key from the symbol table.
*/
public void put(Key key, Value val) {
if (key == null)
throw new IllegalArgumentException("argument key to put() is null");
Node u = insert(root, key, val, height);
n++;
if (u == null)
return;
// need to split root
Node t = new Node(2);
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}
private Node insert(Node h, Key key, Value val, int ht) {
int j;
Entry t = new Entry(key, val, null);
// external node
if (ht == 0) {
for (j = 0; j < h.m; j++) {
if (less(key, h.children[j].key))
break;
}
}
// internal node
else {
for (j = 0; j < h.m; j++) {
if ((j + 1 == h.m) || less(key, h.children[j + 1].key)) {
Node u = insert(h.children[j++].next, key, val, ht - 1);
if (u == null)
return null;
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
for (int i = h.m; i > j; i--)
h.children[i] = h.children[i - 1];
h.children[j] = t;
h.m++;
if (h.m < M)
return null;
else
return split(h);
}
// split node in half
private Node split(Node h) {
Node t = new Node(M / 2);
h.m = M / 2;
for (int j = 0; j < M / 2; j++)
t.children[j] = h.children[M / 2 + j];
return t;
}
/**
* Returns a string representation of this B-tree (for debugging).
*/
public String toString() {
return toString(root, height, "") + "\n";
}
private String toString(Node h, int ht, String indent) {
StringBuilder s = new StringBuilder();
Entry[] children = h.children;
if (ht == 0) {
for (int j = 0; j < h.m; j++) {
s.append(indent + children[j].key + " " + children[j].val + "\n");
}
} else {
for (int j = 0; j < h.m; j++) {
if (j > 0)
s.append(indent + "(" + children[j].key + ")\n");
s.append(toString(children[j].next, ht - 1, indent + " "));
}
}
return s.toString();
}
// comparison functions - make Comparable instead of Key to avoid casts
private boolean less(Comparable k1, Comparable k2) {
return k1.compareTo(k2) < 0;
}
private boolean eq(Comparable k1, Comparable k2) {
return k1.compareTo(k2) == 0;
}
}
BSTs Boot Camp
Validate BST
Given a binary tree, determine if it is a valid binary search tree (BST).
Example 1: 2 / \ 1 3 Binary tree [2,1,3], return true. Example 2: 1 / \ 2 3 Binary tree [1,2,3], return false.
public boolean isValidBST(TreeNode root) {
return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean isValidBST(TreeNode root, long minVal, long maxVal) {
if (root == null)
return true;
if (root.val >= maxVal || root.val <= minVal)
return false;
return isValidBST(root.left, minVal, root.val) && isValidBST(root.right, root.val, maxVal);
}
Find LCA of BST
Also called: Lowest Common Ancestor of a Binary Search Tree
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
} else if (root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
} else {
return root;
}
}
Get Min Difference
Given a binary search tree with non-negative values, find the minimum absolute difference between values of any two nodes.
private TreeNode prev;
public int minDifference(TreeNode node) {
if (node == null)
return Integer.MAX_VALUE;
int minDiff = minDifference(node.left);
if (prev != null)
minDiff = Math.min(minDiff, Math.abs(node.val - prev.val));
prev = node;
minDiff = Math.min(minDiff, minDifference(node.right));
return minDiff;
}
Lookup Range in BST
Write a program that takes as input a BST and an interval and returns the BST keys that lie in the interval.
The traversal spends O(h) time visiting the first two subsets, and O(m) time traversing the third subset – each edge is visited twice, once downwards, once upwards. Therefore the total time complexity is O(m+h).
public List<Integer> rangeLookupInBST(TreeNode tree, Interval interval) {
List<Integer> result = new ArrayList<>();
rangeLookupInBST(tree, interval, result);
return result;
}
// in-order traversal
private void rangeLookupInBST(TreeNode tree, Interval interval, List<Integer> result) {
if (tree == null)
return;
if (interval.left <= tree.val && tree.val <= interval.right) {
rangeLookupInBST(tree.left, interval, result);
result.add(tree.val);
rangeLookupInBST(tree.right, interval, result);
} else if (interval.left > tree.val) {
rangeLookupInBST(tree.right, interval, result);
} else {
rangeLookupInBST(tree.left, interval, result);
}
}
Find One Closest Value
Given a non-empty binary search tree and a target value, find the value in the BST that is closest to the target.
public int closestValue(TreeNode root, double target) {
int result = root.val;
while (root != null) {
if (Math.abs(target - root.val) < Math.abs(target - result))
result = root.val;
root = root.val > target ? root.left : root.right;
}
return result;
}
Find K Closest Values
Given a non-empty binary search tree and a target value, find k values in the BST that are closest to the target.
We can perform a in-order traversal. Another variant is to find K largest values, we need perform an reverse in-order traversal.
public List<Integer> closestKValues(TreeNode root, double target, int k) {
LinkedList<Integer> list = new LinkedList<Integer>();
closestKValues(list, root, target, k);
return list;
}
// in-order traverse
private boolean closestKValues(LinkedList<Integer> list, TreeNode root, double target, int k) {
if (root == null)
return false;
if (closestKValues(list, root.left, target, k))
return true;
if (list.size() == k) {
if (Math.abs(list.getFirst() - target) < Math.abs(root.val - target))
return true;
else
list.removeFirst();
}
list.addLast(root.val);
return closestKValues(list, root.right, target, k);
}
Largest BST Subtree
Given a binary tree, find the largest subtree which is a Binary Search Tree (BST), where largest means subtree with largest number of nodes in it.
Note: A subtree must include all of its descendants.
Here's an example: 10 / \ 5 15 / \ \ 1 8 7 The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.
public int largestBSTSubtree(TreeNode root) {
if (root == null)
return 0;
if (root.left == null && root.right == null)
return 1;
if (isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE))
return countTreeNode(root);
return Math.max(largestBSTSubtree(root.left), largestBSTSubtree(root.right));
}
private int countTreeNode(TreeNode root) {
if (root == null)
return 0;
if (root.left == null && root.right == null)
return 1;
return 1 + countTreeNode(root.left) + countTreeNode(root.right);
}
Find Distance in BST
Give a list of unique integers, try build a tree based on the insert order, and find the distance between two nodes.
public static int bstDistance(int[] values, int n, int node1, int node2) {
TreeNode tree = constructBST(values);
return distanceBetween(tree, node1, node2);
}
private static TreeNode constructBST(int[] values) {
if (values == null || values.length == 0)
return null;
TreeNode root = null;
for (int i = 0; i < values.length; i++) {
root = insert(root, values[i]);
}
return root;
}
private static TreeNode insert(TreeNode root, int key) {
if (root == null) {
root = new TreeNode(key);
} else if (root.val > key) {
root.left = insert(root.left, key);
} else {
root.right = insert(root.right, key);
}
return root;
}
private static int distanceBetween(TreeNode root, int p, int q) {
if (root == null)
return 0;
if (root.val > p && root.val > q) {
return distanceBetween(root.left, p, q);
} else if (root.val < p && root.val < q) {
return distanceBetween(root.right, p, q);
} else {
return distanceFromRoot(root, p) + distanceFromRoot(root, q);
}
}
private static int distanceFromRoot(TreeNode root, int x) {
if (root.val == x)
return 0;
else
return 1 + (root.val > x ? distanceFromRoot(root.left, x) : distanceFromRoot(root.right, x));
}
public static void main(String[] args) {
System.out.println(bstDistance(new int[] { 5, 6, 3, 1, 2, 4 }, 6, 2, 4));
}
Convert Traversal Data to BST
Suppose you are given the sequence in which keys are visited in an preorder traversal of a BST, and all keys are distinct. Can you reconstruct the BST from the sequence?
The complexity is O(n)
private Integer rootIdx;
public TreeNode rebuildBSTFromPreorder(List<Integer> preorderSequence) {
rootIdx = 0;
return rebuildBSTFromPreorderOnValueRange(preorderSequence, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
private TreeNode rebuildBSTFromPreorderOnValueRange(List<Integer> preorderSequence, Integer lowerBound,
Integer upperBound) {
if (rootIdx == preorderSequence.size())
return null;
Integer root = preorderSequence.get(rootIdx);
if (root < lowerBound || root > upperBound)
return null;
rootIdx++;
TreeNode leftSubtree = rebuildBSTFromPreorderOnValueRange(preorderSequence, lowerBound, root);
TreeNode rightSubtree = rebuildBSTFromPreorderOnValueRange(preorderSequence, root, upperBound);
return new TreeNode(root, leftSubtree, rightSubtree);
}
Convert Sorted List to BST
Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
Use slow-fast traversal to get the middle element and make that the root. left side of the list forms left sub-tree and right side of the middle element forms the right sub-tree.
You can also find the middle element using int mid = start + ((end - start) / 2)
public TreeNode sortedListToBST(ListNode head) {
if (head == null)
return null;
return convertToBST(head, null);
}
private TreeNode convertToBST(ListNode head, ListNode tail) {
ListNode slow = head;
ListNode fast = head;
if (head == tail)
return null;
while (fast != tail && fast.next != tail) {
fast = fast.next.next;
slow = slow.next;
}
TreeNode thead = new TreeNode(slow.val);
thead.left = convertToBST(head, slow);
thead.right = convertToBST(slow.next, tail);
return thead;
}
Binary Search Tree Iterator
Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.
Calling next() will return the next smallest number in the BST.
Note: next() and hasNext() should run in average O(1) time and uses O(h) memory, where h is the height of the tree.
public class BSTIterator {
final Deque<TreeNode> path;
public BSTIterator(TreeNode root) {
path = new ArrayDeque<>();
buildPathToLeftmostChild(root);
}
public boolean hasNext() {
return !path.isEmpty();
}
public int next() {
TreeNode node = path.pop();
buildPathToLeftmostChild(node.right);
return node.val;
}
private void buildPathToLeftmostChild(TreeNode node) {
TreeNode cur = node;
while (cur != null) {
path.push(cur);
cur = cur.left;
}
}
}
Binary Tree Upside Down
Given a binary tree where all the right nodes are either leaf nodes with a sibling (a left node that shares the same parent node) or empty, flip it upside down and turn it into a tree where the original right nodes turned into left leaf nodes. Return the new root.
Example:
Input: [1,2,3,4,5]
1
/ \
2 3
/ \
4 5
Output: return the root of the binary tree [4,5,2,#,#,3,1]
4
/ \
5 2
/ \
3 1
public TreeNode upsideDownBinaryTree(TreeNode root) {
if (root == null) {
return root;
}
Stack<TreeNode> stack = new Stack<>();
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode newRoot = stack.pop();
TreeNode cur = newRoot;
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
cur.left = node.right;
cur.right = node;
node.left = null;
node.right = null;
cur = node;
}
return newRoot;
}
Min Distance in K Sorted Arrays
For example, if the three arrays are [5, 10, 15], [3, 6, 9, 12, 15] and [8, 16, 24], then 15, 15, 16 lie in the smallest possible interval which is 1.
We can begin with the first element of each arrays, [5, 3, 8]. The smallest interval whose left end point is 3 has length 8 - 3 = 5. The element after 3 is 6, so we continue with the triple (5, 6, 8). The smallest interval whose left end point is 5 has length 8 - 5 = 3. The element after 5 is 10, so we continue with the triple (10, 6, 8)…
public int minDistanceInKSortedArrays(List<List<Integer>> sortedArrays) {
int result = Integer.MAX_VALUE;
// int[3]: arrayIdx, valueIdx, value
NavigableSet<int[]> currentHeads = new TreeSet<>((a, b) -> (a[2] - b[2] == 0 ? a[0] - b[0] : a[2] - b[2]));
for (int i = 0; i < sortedArrays.size(); i++) {
currentHeads.add(new int[] { i, 0, sortedArrays.get(i).get(0) });
}
while (true) {
result = Math.min(result, currentHeads.last()[2] - currentHeads.first()[2]);
int[] data = currentHeads.pollFirst();
// Return if some array has no remaining elements.
int nextValueIdx = data[1] + 1;
if (nextValueIdx >= sortedArrays.get(data[0]).size()) {
return result;
}
currentHeads.add(new int[] { data[0], nextValueIdx, sortedArrays.get(data[0]).get(nextValueIdx) });
}
}
Employee Free Time
We are given a list schedule of employees, which represents the working time for each employee.
Each employee has a list of non-overlapping Intervals, and these intervals are in sorted order.
Return the list of finite intervals representing common, positive-length free time for all employees, also in sorted order.
Example 1:
Input: schedule = [[[1,2],[5,6]],[[1,3]],[[4,10]]]
Output: [[3,4]]
Explanation: There are a total of three employees, and all common
free time intervals would be [-inf, 1], [3, 4], [10, inf].
We discard any intervals that contain inf as they aren't finite.
Example 2:
Input: schedule = [[[1,3],[6,7]],[[2,4]],[[2,5],[9,12]]]
Output: [[5,6],[7,9]]
// Time complexity: nlog(k), space complexity: k
public List<Interval> employeeFreeTime(List<List<Interval>> schedule) {
Queue<int[]> queue = new PriorityQueue<>((a, b) -> schedule.get(a[0]).get(a[1]).start - schedule.get(b[0]).get(b[1]).start);
for (int i = 0; i < schedule.size(); i++) {
queue.add(new int[] { i, 0 });
}
List<Interval> result = new ArrayList<>();
int prevEnd = schedule.get(queue.peek()[0]).get(queue.peek()[1]).start;
while (!queue.isEmpty()) {
int[] index = queue.poll();
Interval interval = schedule.get(index[0]).get(index[1]);
if (interval.start > prevEnd) {
result.add(new Interval(prevEnd, interval.start));
}
prevEnd = Math.max(prevEnd, interval.end);
if (schedule.get(index[0]).size() > index[1] + 1) {
queue.add(new int[] { index[0], index[1] + 1 });
}
}
return result;
}
Design Client Credits Info
Consider a server that a large number of clients connect to. Each client is identified by a string. Each client has a “credit”, which is a non-negative integer value. The server needs to maintain a data structure to which clients can be added, removed, queried or updated. In addition, the server needs to be able to add a specified number of credits to all clients simultaneously.
The time complexity to insert and remove is dominated by the BST, i.e., O(logn). Lookup and add-to-all operate only on the hash table, and have O(1) time complexity. NavigableMap uses caching to perform max in O(1) time.
public class ClientsCreditsInfo {
private int offset = 0; // track increasing credit for all!
private Map<String, Integer> clientToCredit = new HashMap<>();
private NavigableMap<Integer, Set<String>> creditToClients = new TreeMap<>();
public void insert(String clientID, int credit) {
remove(clientID); // always remove first!
int normalizedCredit = credit - offset;
clientToCredit.put(clientID, normalizedCredit);
Set<String> set = creditToClients.get(normalizedCredit);
if (set == null) {
set = new HashSet<>();
creditToClients.put(normalizedCredit, set);
}
set.add(clientID);
}
public boolean remove(String clientID) {
Integer clientCredit = clientToCredit.get(clientID);
if (clientCredit != null) {
creditToClients.get(clientCredit).remove(clientID);
if (creditToClients.get(clientCredit).isEmpty()) {
creditToClients.remove(clientCredit);
}
clientToCredit.remove(clientID);
return true;
}
return false;
}
public int lookup(String clientID) {
Integer clientCredit = clientToCredit.get(clientID);
return clientCredit == null ? -1 : clientCredit + offset;
}
// increment the credit count for all current clients
public void addAll(int credit) {
offset += credit;
}
public String max() {
return creditToClients.isEmpty() ? "" : creditToClients.lastEntry().getValue().iterator().next();
}
}
Segment Tree
Segment Tree is used in cases where there are multiple range queries on array and modifications of elements of the same array. For example, finding the sum of all the elements in an array from indices L to R, or finding the minimum of all the elements in an array from indices L to R.
Segment Tree is basically a binary tree used for storing the intervals or segments. Each node in the Segment Tree represents an interval. Consider an array A of size N and a corresponding segment tree T:
- The root of T represents the whole array A[0:N-1].
- Each leaf represents a single element A[i] such that 0<=i<N.
- The internal nodes represent the union of elementary intervals A[i:j] where 0<=i<j<N.
- In each step, the segment is divided into half and the two children represent those two halves. So the height of the tree is log(2)N, a total number of nodes are n + n/2 + n/4 + n/8 + … + 1 ≈ 2n, (more accurate: 2 * 2 ^ log2(n) + 1)
- Furthermore, we can use Lazy Propagation to reduce wasteful computations and process nodes on-demand. We can use another array lazy[] with the same size of tree[] to represent a lazy node.
tree[treeIndex] += (hi - lo + 1) * lazy[treeIndex]; // tree high tree[treeIndex] += (hi - lo + 1) * val;
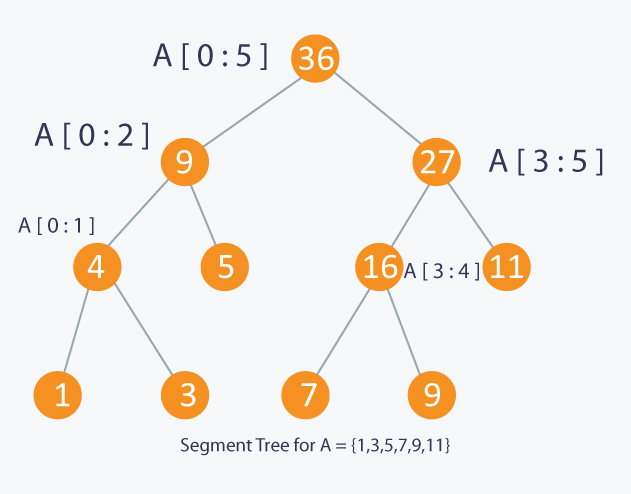
public class SegmentTree {
private Node[] heap;
private int[] array;
private int size;
// Time-complexity: O(n*log(n))
public SegmentTree(int[] array) {
this.array = Arrays.copyOf(array, array.length);
// The max size of this array is about 2 * 2 ^ log2(n) + 1
size = (int) (2 * Math.pow(2.0, Math.floor((Math.log((double) array.length) / Math.log(2.0)) + 1)));
heap = new Node[size];
build(1, 0, array.length); // 1-based tree/heap
}
public int size() {
return array.length;
}
// Initialize the Nodes of the Segment tree
private void build(int v, int from, int size) {
Node node = new Node();
heap[v] = node;
node.from = from;
node.to = from + size - 1;
if (size == 1) {
node.sum = array[from];
node.min = array[from];
} else {
int len = size / 2;
build(2 * v, from, len);
build(2 * v + 1, from + len, size - len);
node.sum = heap[2 * v].sum + heap[2 * v + 1].sum;
node.min = Math.min(heap[2 * v].min, heap[2 * v + 1].min);
}
}
// Range sum query time-omplexity: O(log(n))
public int rsq(int from, int to) {
return rsq(1, from, to);
}
private int rsq(int v, int from, int to) {
Node node = heap[v];
// If you did a range update that contained this node, you can infer the Sum without going down the tree
if (node.pendingVal != null && contains(node.from, node.to, from, to)) {
return (to - from + 1) * node.pendingVal;
}
if (contains(from, to, node.from, node.to)) {
return node.sum;
}
if (intersects(from, to, node.from, node.to)) {
propagate(v);
int leftSum = rsq(2 * v, from, to);
int rightSum = rsq(2 * v + 1, from, to);
return leftSum + rightSum;
}
return 0;
}
/**
* Range Min Query Time-Complexity: O(log(n))
*/
public int rMinQ(int from, int to) {
return rMinQ(1, from, to);
}
private int rMinQ(int v, int from, int to) {
Node node = heap[v];
// If you did a range update that contained this node, you can infer the Min value without going down the tree
if (node.pendingVal != null && contains(node.from, node.to, from, to)) {
return node.pendingVal;
}
if (contains(from, to, node.from, node.to)) {
return heap[v].min;
}
if (intersects(from, to, node.from, node.to)) {
propagate(v);
int leftMin = rMinQ(2 * v, from, to);
int rightMin = rMinQ(2 * v + 1, from, to);
return Math.min(leftMin, rightMin);
}
return Integer.MAX_VALUE;
}
/**
* Range Update Operation. With this operation you can update either one position or a range of
* positions with a given number. The update operations will update the less it can to update the
* whole range (Lazy Propagation). The values will be propagated lazily from top to bottom of the
* segment tree. This behavior is really useful for updates on portions of the array
*
* Time-Complexity: O(log(n))
*
*/
public void update(int from, int to, int value) {
update(1, from, to, value);
}
private void update(int v, int from, int to, int value) {
// The Node of the heap tree represents a range of the array with bounds: [n.from, n.to]
Node node = heap[v];
/**
* If the updating-range contains the portion of the current Node We lazily update it. This means We
* do NOT update each position of the vector, but update only some temporal values into the Node;
* such values into the Node will be propagated down to its children only when they need to.
*/
if (contains(from, to, node.from, node.to)) {
change(node, value);
}
if (node.size() == 1)
return;
if (intersects(from, to, node.from, node.to)) {
/**
* Before keeping going down to the tree We need to propagate the the values that have been
* temporally/lazily saved into this Node to its children So that when We visit them the values are
* properly updated
*/
propagate(v);
update(2 * v, from, to, value);
update(2 * v + 1, from, to, value);
node.sum = heap[2 * v].sum + heap[2 * v + 1].sum;
node.min = Math.min(heap[2 * v].min, heap[2 * v + 1].min);
}
}
// Propagate temporal values to children
private void propagate(int v) {
Node node = heap[v];
if (node.pendingVal != null) {
change(heap[2 * v], node.pendingVal);
change(heap[2 * v + 1], node.pendingVal);
node.pendingVal = null; // unset the pending propagation value
}
}
// Save the temporal values that will be propagated lazily
private void change(Node n, int value) {
n.pendingVal = value;
n.sum = n.size() * value;
n.min = value;
array[n.from] = value;
}
// Test if the range1 contains range2
private boolean contains(int from1, int to1, int from2, int to2) {
return from2 >= from1 && to2 <= to1;
}
// check inclusive intersection, test if range1[from1, to1] intersects range2[from2, to2]
private boolean intersects(int from1, int to1, int from2, int to2) {
return from1 <= from2 && to1 >= from2 // (.[..)..] or (.[...]..)
|| from1 >= from2 && from1 <= to2; // [.(..]..) or [..(..)..
}
// The Node class represents a partition range of the array.
static class Node {
int sum, min;
int from, to;
// Store the value that will be propagated lazily
Integer pendingVal = null;
int size() {
return to - from + 1;
}
}
public static void main(String[] args) {
int[] nums = { 1, 4, 3, 6, 7, 5, 2, 0, 9, 8 };
SegmentTree solution = new SegmentTree(nums);
assert solution.rsq(1, 7) == 27;
solution.update(2, 2, 5);
assert solution.rsq(1, 7) == 29;
}
}
Below is the concise iterative version of Segment Tree.
public class RangeSumQuery2 {
private int n;
private int[] tree;
public RangeSumQuery2(int[] nums) {
if (nums.length > 0) {
n = nums.length;
tree = new int[2 * n]; // 2n extra space
buildTree(nums);
}
}
private void buildTree(int[] nums) {
for (int i = n, j = 0; i < 2 * n; i++, j++)
tree[i] = nums[j];
for (int i = n - 1; i >= 0; i--)
tree[i] = tree[i * 2] + tree[i * 2 + 1];
}
public void update(int pos, int val) {
pos += n;
tree[pos] = val;
while (pos > 0) {
int left = pos;
int right = pos;
if (pos % 2 == 0)
right = pos + 1;
else
left = pos - 1;
tree[pos / 2] = tree[left] + tree[right];
pos /= 2;
}
}
public int sumRange(int l, int r) {
l += n; // get leaf with value l;
r += n; // get leaf with value r;
int sum = 0;
while (l <= r) {
if ((l % 2) == 1) {
sum += tree[l];
l++;
}
if ((r % 2) == 0) {
sum += tree[r];
r--;
}
l /= 2;
r /= 2;
}
return sum;
}
}
Sqrt Decomposition
The above segment tree issue can also be resolved by using Sqrt Decomposition. The idea is to split the array blocks with length of \(\sqrt n\). Then we calculate the sum of each block and store it in auxiliary memory b. To query RSQ(i, j), we will add the sums of all the blocks lying inside and those that partially overlap with range [i…j].
Time complexity: \(O(n)\) - preprocessing; \(O(\sqrt n)\) - range sum query; \(O(1)\) - update value
public class RangeSumQuery {
private int[] nums;
private int length;
private int[] blocks;
public RangeSumQuery(int[] nums) {
this.nums = nums;
double l = Math.sqrt(nums.length);
length = (int) Math.ceil(nums.length / l);
blocks = new int[length];
for (int i = 0; i < nums.length; i++) {
blocks[i / length] += nums[i];
}
}
public int sumRange(int i, int j) {
int sum = 0;
int startBlock = i / length;
int endBlock = j / length;
if (startBlock == endBlock) {
for (int k = i; k <= j; k++)
sum += nums[k];
} else {
for (int k = i; k <= (startBlock + 1) * length - 1; k++)
sum += nums[k];
for (int k = startBlock + 1; k <= endBlock - 1; k++)
sum += blocks[k];
for (int k = endBlock * length; k <= j; k++)
sum += nums[k];
}
return sum;
}
public void update(int i, int val) {
blocks[i / length] += val - nums[i];
nums[i] = val;
}
}