Dynamic Programming
Dynamic programming (DP) is mostly just a matter of taking a recursive algorithm and finding the overlapping subproblems (that is, the repeated calls). You then cache those results for future recursive calls.
All recursive algorithms can be implemented iteratively (still use cache), although sometimes the code to do so is much more complex. Each recursive call adds a new layer to the stack, which means that if your algorithm recurses to a depth of n, it uses at least O(n) memory.
When DP is implemented recursively the cache is typically a dynamic data structure such as a hash table or a BST; when it’s implemented iteratively the cache is usually a one- or multi-dimensional array.
To illustrate the idea underlying DP, let’s walk through the approaches to compute the nth Fibonacci number.
Fibonacci Numbers
Mathematically, the nth Fibonacci number is given by the equation: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1. The first few Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21,…
Simple Recursive Implementation
We can start with a simple recursive implementation. This gives us a runtime of roughly O(2^n), an exponential runtime.
public static int fibonacciI(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
return fibonacciI(n - 1) + fibonacciI(n - 2);
}
Top-Down Dynamic Programming
We still use top-down dynamic programming, but with memorization this time! The runtime is roughly O(n) since we are caching the result and use it later.
public static int fibonacciII(int i) {
return fibonacciII(i, new int[i + 1]);
}
public static int fibonacciII(int n, int[] memo) {
if (n == 0)
return 0;
if (n == 1)
return 1;
if (memo[n] == 0) {
memo[n] = fibonacciII(n - 1, memo) + fibonacciII(n - 2, memo);
}
return memo[n];
}
Bottom-Up Dynamic Programming
Let’s change it to bottom-up dynamic programming, with memorization too! This give us the same O(n) runtime.
public static int fibonacciIII(int n) {
if (n == 0)
return 0;
int[] memo = new int[n + 1];
memo[0] = 0;
memo[1] = 1;
for (int i = 2; i <= n; i++) {
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
}
Achieve The Best Complexity
We can even get rid of the memo table, to achieve O(n) time and O(1) space.
public static int fibonacciVI(int n) {
if (n == 0)
return 0;
int a = 0;
int b = 1;
for (int i = 2; i <= n; i++) {
int c = a + b;
a = b;
b = c;
}
return b;
}
DP Boot Camp
Climbing Stair
You are climbing a stair case. It takes n steps to reach to the top. Each time you can climb 1 to k steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Use top-down DP with memorization. The time complexity is O(kn), benefit from memorization, the space complexity is O(n)
public static int climbStairs(int n, int k) {
return climbStairs(n, k, new int[n + 1]);
}
private static int climbStairs(int n, int k, int[] memo) {
if (n < 0)
return 0;
else if (n == 0)
return 1; // use one or zero?
else if (n == 1)
return 1;
if (memo[n] == 0) {
for (int i = 1; i <= Math.min(k, n); i++) {
memo[n] += climbStairs(n - i, k, memo);
}
}
return memo[n];
}
Min Cost Climbing Stairs
On a staircase, the i-th step has some non-negative cost cost[i] assigned (0 indexed).
Once you pay the cost, you can either climb one or two steps. You need to find minimum cost to reach the top of the floor, and you can either start from the step with index 0, or the step with index 1.
Example 1:
Input: cost = [10, 15, 20]
Output: 15
Explanation: Cheapest is start on cost[1], pay that cost and go to the top.
public int minCostClimbingStairs(int[] cost) {
int prevCost = 0, currCost = 0;
for (int c : cost) {
int newCost = c + Math.min(prevCost, currCost);
prevCost = currCost;
currCost = newCost;
}
return Math.min(prevCost, currCost);
}
Max Money Rob House
The only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Example:
Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
public int robHouses(int[] nums) {
int prevMax = 0;
int currMax = 0;
for (int x : nums) {
int temp = currMax;
currMax = Math.max(prevMax + x, currMax);
prevMax = temp;
}
return currMax;
}
Delete and Earn
Given an array nums of integers, you can perform operations on the array.
In each operation, you pick any nums[i] and delete it to earn nums[i] points. After, you must delete every element equal to nums[i] - 1 or nums[i] + 1.
You start with 0 points. Return the maximum number of points you can earn by applying such operations.
Example 1:
Input: nums = [3, 4, 2]
Output: 6
Explanation:
Delete 4 to earn 4 points, consequently 3 is also deleted.
Then, delete 2 to earn 2 points. 6 total points are earned.
public int deleteAndEarn(int[] nums) {
int max = Arrays.stream(nums).max();
int[] sum = new int[max];
// perform a radix sort, sum the same num
for (int i = 0; i < nums.length; i++) {
sum[nums[i]] += nums[i];
}
// depends on previous sum or the prior plus the current.
for (int i = 2; i < sum.length; i++) {
// sum[i] carries forward the accumulated total
sum[i] = Math.max(sum[i - 1], sum[i - 2] + sum[i]);
}
return sum[sum.length - 1];
}
Partition Array Equally
Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
Example 1:
Input: [1, 5, 11, 5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
Example 2:
Input: [1, 2, 3, 5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.
Actually, this is a 0/1 knapsack problem, for each number, you can pick it or not. Let us assume dp[i][j] means whether the specific sum j can be gotten from the first i numbers. If we can pick such a series of numbers for 0-i whose sum is j, dp[i][j] is true, otherwise it is false.
Base case: dp[0][0] is true; (zero number consists of sum 0 is true)
Transition function: For each number, if we don’t pick it, dp[i][j] = dp[i-1][j], which means if the first i-1 elements has made it to j, dp[i][j] would also make it to j (we can just ignore nums[i]). If we pick nums[i], dp[i][j] = dp[i-1][j-nums[i]], which represents that j is composed of the current value nums[i] and the remaining composed of other previous numbers. Thus, the transition function is dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]
And here we can just use one dimension array to cache the status
First, we already approved the sum of whole set can be divided by the target number. dp[i][j] = true means the first i numbers can be partitioned evenly to the target number, if we add another number to the set, this number must equal to the target. dp[i][j] = false and we add another number x, the dp[i][j-x] == true,also means the whole set can be partitioned.
We could further optimize it to use 1D array, as for any array element i, we need results of the previous iteration (i - 1) only.
// This is only apply for 2 groups, NOT for K groups
public boolean canPartitionEqually(int[] nums) {
int subgroups = 2; // partition equally!
int sum = Arrays.stream(nums).sum();
if (sum % subgroups != 0)
return false;
int target = sum / subgroups;
boolean[] dp = new boolean[target + 1];
dp[0] = true;
for (int num : nums) {
for (int i = target; i >= num; i--) {
// true once reached to the dp[0]!
dp[i] |= dp[i - num]; // not pick it or pick it!
}
}
return dp[target];
}
Partition to K Equal Sum Subsets
Given an array of integers nums and a positive integer k, find whether it’s possible to divide this array into k non-empty subsets whose sums are all equal.
Example 1: Input: nums = [4, 3, 2, 3, 5, 2, 1], k = 4 Output: True Explanation: It’s possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
Solution #0: DFS with Backtrack
public boolean canPartitionKSubsets(int[] nums, int k) {
int sum = 0;
for (int n : nums)
sum += n;
if (sum % k != 0)
return false;
int target = sum / k;
return partitionDFS(0, k, 0, target, nums, new boolean[nums.length]);
}
// DFS with Backtrack
public boolean partitionDFS(int i, int k, int sum, int target, int[] nums, boolean[] visited) {
if (k == 0)
return true;
if (target == sum)
// start a new group
return partitionDFS(0, k - 1, 0, target, nums, visited);
if (i == nums.length || sum > target)
return false;
// move forward without using current value
boolean result = partitionDFS(i + 1, k, sum, target, nums, visited);
if (!result && !visited[i]) {
// dfs with using current value
visited[i] = true;
result = partitionDFS(i + 1, k, sum + nums[i], target, nums, visited);
visited[i] = false;
}
return result;
}
Solution #1: Search by Constructing Subset Sums
Time Complexity: O(k^(N−k)k!), where N is the length of nums, and k is as given. As we skip additional zeroes in groups, naively we will make O(k!) calls to search, then an additional O(k^(N−k)) calls after every element of groups is nonzero.
Space Complexity: O(N), the space used by recursive calls to search in our call stack.
public boolean canPartitionKSubsets(int[] nums, int k) {
int sum = Arrays.stream(nums).sum();
if (sum % k > 0)
return false;
int target = sum / k;
// some tricks to speedup, not necessary
Arrays.sort(nums);
int index = nums.length - 1;
if (nums[index] > target)
return false;
while (index >= 0 && nums[index] == target) {
index--;
k--;
}
return search(new int[k], index, nums, target);
}
// fill group with the large number first!
private boolean search(int[] groups, int index, int[] nums, int target) {
if (index < 0)
return true;
int v = nums[index--];
for (int i = 0; i < groups.length; i++) {
if (groups[i] + v <= target) {
groups[i] += v;
if (search(groups, index, nums, target))
return true;
groups[i] -= v; // back track
}
// greatly reduces repeated work
if (groups[i] == 0) // expect at least 1 number
break;
}
return false;
}
Solution #2: Dynamic Programming on Subsets of Input
Time Complexity: O(N2^N), where N is the length of nums. There are 2^N states of used (or state in our bottom-up variant), and each state performs O(N) work searching through nums.
Space Complexity: O(2^N), the space used by memo (or dp, total in our bottom-up variant).
public boolean canPartitionKSubsets2(int[] nums, int k) {
int N = nums.length;
Arrays.sort(nums);
int sum = Arrays.stream(nums).sum();
int target = sum / k;
if (sum % k > 0 || nums[N - 1] > target)
return false;
boolean[] dp = new boolean[1 << N];
dp[0] = true;
int[] total = new int[1 << N];
for (int state = 0; state < (1 << N); state++) {
if (!dp[state])
continue;
for (int i = 0; i < N; i++) {
int future = state | (1 << i);
if (state != future && !dp[future]) {
if (nums[i] <= target - (total[state] % target)) {
dp[future] = true;
total[future] = total[state] + nums[i];
} else {
break;
}
}
}
}
return dp[(1 << N) - 1];
}
Partition Array for Maximum Sum
/**
* Given an integer array arr, partition the array into (contiguous) subarrays of length at most k.
* After partitioning, each subarray has their values changed to become the maximum value of that
* subarray.
*
* Return the largest sum of the given array after partitioning. Test cases are generated so that
* the answer fits in a 32-bit integer.
*
* <pre>
* Input: arr = [1,15,7,9,2,5,10], k = 3
* Output: 84
* Explanation: arr becomes [15,15,15,9,10,10,10]
* </pre>
*
* Solution: Bottom up DP, O(n*k) O(n)
*/
public int maxSumAfterPartitioning(int[] arr, int k) {
int len = arr.length;
int[] dp = new int[len + 1];
for (int i = len - 1; i >= 0; i--) {
int ans = Integer.MIN_VALUE, max = Integer.MIN_VALUE;
for (int j = 0; j < k && i + j < len; j++) {
max = Math.max(max, arr[i + j]);
ans = Math.max(ans, max * (j + 1) + dp[i + j + 1]);
}
dp[i] = ans;
}
return dp[0];
}
Partition Array into Disjoint Intervals
/**
* Given an integer array nums, partition it into two (contiguous) subarrays left and right so that:
*
* Every element in left is less than or equal to every element in right. left and right are
* non-empty. left has the smallest possible size. Return the length of left after such a
* partitioning.
*
* <pre>
* Input: nums = [5,0,3,8,6]
* Output: 3
* Explanation: left = [5,0,3], right = [8,6]
* </pre>
*
* Solution:
*
* As we iterate over nums we can keep track of the largest number seen so far that must be in the
* left subarray (curr_max) and the largest number seen so far that could possibly be in the left
* subarray (possible_max). Whenever a number is less than curr_max then that number and all of the
* numbers to its left must belong to the left subarray, and curr_max becomes the largest number
* seen so far (possible_max).
*/
public int partitionDisjoint(int[] nums) {
int currMax = nums[0];
int possibleMax = nums[0];
int length = 1;
for (int i = 1; i < nums.length; ++i) {
if (nums[i] < currMax) {
length = i + 1;
currMax = possibleMax;
} else {
possibleMax = Math.max(possibleMax, nums[i]);
}
}
return length;
}
Largest Sum of Averages
We partition a row of numbers A into at most K adjacent (non-empty) groups, then our score is the sum of the average of each group. What is the largest score we can achieve?
Note that our partition must use every number in A, and that scores are not necessarily integers.
Example:
Input:
A = [9,1,2,3,9]
K = 3
Output: 20
Explanation:
The best choice is to partition A into [9], [1, 2, 3], [9]. The answer is 9 + (1 + 2 + 3) / 3 + 9 = 20.
We could have also partitioned A into [9, 1], [2], [3, 9], for example.
That partition would lead to a score of 5 + 2 + 6 = 13, which is worse.
Solution:
The best score partitioning A[i:] into at most K parts depends on answers to partitioning A[j:] (j > i) into less parts. We can use dynamic programming as the states form a directed acyclic graph.
Let dp(i, k) be the best score partition A[i:] into at most K parts. In total, our recursion in the general case is dp(i, k) = max(average(i, N), max_{j > i}(average(i, j) + dp(j, k-1))).
Time Complexity: O(K∗N^2), where N is the length of A.
// bottom up recursion
public double largestSumOfAverages(int[] A, int K) {
int N = A.length;
// accumulatively sum
double[] P = new double[N + 1];
for (int i = 0; i < N; i++)
P[i + 1] = P[i] + A[i];
// starts with base case, average till to end
double[] dp = new double[N];
for (int i = 0; i < N; i++)
dp[i] = (P[N] - P[i]) / (N - i);
// sum up to K - 1 times, add average's difference
for (int k = 0; k < K - 1; k++)
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
dp[i] = Math.max(dp[i], (P[j] - P[i]) / (j - i) + dp[j]);
return dp[0];
}
Maximum Average Subarray
Given an array consisting of n integers, find the contiguous subarray whose length is greater than or equal to k that has the maximum average value. And you need to output the maximum average value.
Example 1:
Input: [1,12,-5,-6,50,3], k = 4
Output: 12.75
Explanation:
when length is 5, maximum average value is 10.8,
when length is 6, maximum average value is 9.16667.
Thus return 12.75.
Solution: Using Binary Search, Time Complexity is: O(nlog(maxVal−minVal)).
public double findMaxAverage(int[] nums, int k) {
double maxVal = Integer.MIN_VALUE;
double minVal = Integer.MAX_VALUE;
for (int n : nums) {
maxVal = Math.max(maxVal, n);
minVal = Math.min(minVal, n);
}
while (maxVal - minVal > 0.00001) {
double mid = (maxVal + minVal) * 0.5;
if (hasBiggerAverage(nums, mid, k))
minVal = mid;
else
maxVal = mid;
}
return maxVal;
}
private boolean hasBiggerAverage(int[] nums, double mid, int k) {
double sum = 0, prev = 0;
// find whether there is a subarray whose difference's sum is bigger than 0
// ((a1 + a2 + a3 ... + aj) >= j * mid) or ((a1 - mid) + (a2 - mid) + (a3 - mid) + ... + (aj - mid) >= 0)
for (int i = 0; i < k; i++)
sum += nums[i] - mid;
if (sum >= 0)
return true;
for (int i = k; i < nums.length; i++) {
sum += nums[i] - mid;
prev += nums[i - k] - mid;
// Negative prev is not helpful to make a bigger sum
if (prev < 0) {
sum -= prev;
prev = 0;
}
if (sum >= 0)
return true;
}
return false;
}
Max Average Difference
e.g. Given { 1, 2, 3, 4, 5, 7 }, it can be grouped to [[1, 2, 3, 4, 5], [7]].
public static int[][] maxAvgDiffGroups(int[] nums) {
if (nums == null || nums.length == 1)
throw new IllegalArgumentException();
// Don't need to sort if we need continous sub arrays.
Arrays.sort(nums); // sort it first! O(nlog(n))
int total = Arrays.stream(nums).sum();
double maxDiff = Double.MIN_VALUE;
double sumSoFar = nums[0];
int pivot = 0; // included
for (int i = 1; i < nums.length - 1; i++) {
sumSoFar += nums[i];
double currDiff = Math.abs(sumSoFar / (i + 1) - (total - sumSoFar) / (nums.length - (i + 1)));
if (currDiff > maxDiff) {
pivot = i;
maxDiff = currDiff;
}
}
int[][] ans = new int[2][];
ans[0] = Arrays.copyOf(nums, pivot + 1);
ans[1] = Arrays.copyOfRange(nums, pivot + 1, nums.length);
return ans;
}
Split Array With Same Average
/**
* You are given an integer array nums.
*
* You should move each element of nums into one of the two arrays A and B such that A and B are
* non-empty, and average(A) == average(B).
*
* Return true if it is possible to achieve that and false otherwise.
*
* Note that for an array arr, average(arr) is the sum of all the elements of arr over the length of
* arr.
*
* Solution:
*
* Since sum1 / len1 = total / n => sum1 = (len1 * total) / n
*
* So finally our problem is reduced to check each possible length and finding a subsequence of the
* given array of this length such that the sum of the elements in this is equal to sum1 (which has
* a logic of 0/1 knapsack).
*/
public boolean splitArraySameAverage(int[] nums) {
int total = 0;
for (int num : nums) {
total += num;
}
for (int count = 1; count < nums.length - 1; count++) {
if ((total * count) % nums.length == 0) { // Able to split array
if (isPossible(nums, 0, count, (total * count) / nums.length, new HashMap<String, Boolean>())) {
return true;
}
}
}
return false;
}
private boolean isPossible(int[] nums, int i, int count, int sum, Map<String, Boolean> map) {
if (sum == 0 && count == 0)
return true;
if (i == nums.length || count == 0)
return false;
String key = i + "-" + count + "-" + sum;
if (map.containsKey(key))
return map.get(key);
boolean result = isPossible(nums, i + 1, count, sum, map);
if (!result && sum - nums[i] >= 0) {
result = isPossible(nums, i + 1, count - 1, sum - nums[i], map);
}
map.put(key, result);
return result;
}
Largest Plus Sign
In a 2D grid from (0, 0) to (N-1, N-1), every cell contains a 1, except those cells in the given list mines which are 0. What is the largest axis-aligned plus sign of 1s contained in the grid? Return the order of the plus sign. If there is none, return 0.
Example 1:
Input: N = 5, mines = [[4, 2]]; Output: 2
Explanation:
11111
11111
11111
11111
11011
In the above grid, the largest plus sign can only be order 2. One of them is marked in bold.
If we knew the longest possible arm length in each direction from a center, we could know the order of a plus sign at that center. We could find these lengths separately using dynamic programming.
public int orderOfLargestPlusSign(int N, int[][] mines) {
Set<Integer> banned = new HashSet<>();
int[][] dp = new int[N][N];
for (int[] mine : mines)
banned.add(mine[0] * N + mine[1]);
int ans = 0, count;
for (int r = 0; r < N; ++r) {
count = 0;
for (int c = 0; c < N; ++c) {
count = banned.contains(r * N + c) ? 0 : count + 1;
dp[r][c] = count;
}
count = 0;
for (int c = N - 1; c >= 0; --c) {
count = banned.contains(r * N + c) ? 0 : count + 1;
dp[r][c] = Math.min(dp[r][c], count);
}
}
for (int c = 0; c < N; ++c) {
count = 0;
for (int r = 0; r < N; ++r) {
count = banned.contains(r * N + c) ? 0 : count + 1;
dp[r][c] = Math.min(dp[r][c], count);
}
count = 0;
for (int r = N - 1; r >= 0; --r) {
count = banned.contains(r * N + c) ? 0 : count + 1;
dp[r][c] = Math.min(dp[r][c], count);
ans = Math.max(ans, dp[r][c]);
}
}
return ans;
}
Number Of Corner Rectangles
Given a grid where each entry is only 0 or 1, find the number of corner rectangles.
A corner rectangle is 4 distinct 1s on the grid that form an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1s used must be distinct.
Example 1:
Input: grid =
[[1, 0, 0, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 1, 0],
[1, 0, 1, 0, 1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].
NOTE: The number of rows and columns of grid will each be in the range [1, 200].
For each pair of 1s in the new row (say at new_row[i] and new_row[j]), we could create more rectangles where that pair forms the base. The number of new rectangles is the number of times some previous row had row[i] = row[j] = 1.
Let’s call a row to be heavy if it has more than sqrt(N) points. When looking at the next row, if it’s a light row. The number of rectangles created is just the number of pairs of 1s. which is f * (f-1) / 2, This will change the complexity of counting a heavy row form O(C^2) to O(N). There are at most sqrt(N) heavy rows.
Time Complexity: \(N\sqrt N\)
public int countCornerRectangles(int[][] grid) {
int N = 0; // total num of 1s
// convert grid to list in favor of coding
List<List<Integer>> rows = new ArrayList<>();
for (int r = 0; r < grid.length; ++r) {
rows.add(new ArrayList<>());
for (int c = 0; c < grid[r].length; ++c)
if (grid[r][c] == 1) {
rows.get(r).add(c);
N++;
}
}
int sqrtN = (int) Math.sqrt(N);
int ans = 0;
// assume max = 200, 200 * c1 + c2 means an unique pair of 1s
Map<Integer, Integer> count = new HashMap<>();
for (int r = 0; r < rows.size(); ++r) {
// split to 2 process: heavy rows and light rows
if (rows.get(r).size() >= sqrtN) {
Set<Integer> target = new HashSet<>(rows.get(r));
// scan each and every row
for (int r2 = 0; r2 < rows.size(); ++r2) {
// skip the processed heavy rows
if (r2 <= r && rows.get(r2).size() >= sqrtN)
continue;
int found = 0;
for (int c2 : rows.get(r2))
if (target.contains(c2))
found++;
ans += found * (found - 1) / 2;
}
} else {
// scan and track each pair of 1s O(C^2) in this row
for (int i1 = 0; i1 < rows.get(r).size(); ++i1) {
int c1 = rows.get(r).get(i1);
for (int i2 = i1 + 1; i2 < rows.get(r).size(); ++i2) {
int c2 = rows.get(r).get(i2); //
int ct = count.getOrDefault(200 * c1 + c2, 0);
ans += ct;
count.put(200 * c1 + c2, ct + 1);
}
}
}
}
return ans;
}
Final Score Combinations
Write a program that takes a final score and scores for individual plays, and returns the number of combinations of plays that result in the final score.
Let the 2D array A[i][j] store the number of score combinations that result in a total of j, using the i plays of scores. Also, we can simply use 1D array.
public static int combinationsForFinalScore(int finalScore, List<Integer> playScores) {
int[] dp = new int[finalScore + 1];
dp[0] = 1; // One way to reach 0 score without any of plays.
for (int i = 0; i < playScores.size(); ++i) {
int playScore = playScores.get(i);
for (int j = 1; j <= finalScore; ++j) {
int withoutThisPlay = i == 0 ? 0 : dp[j];
int withThisPlay = j >= playScore ? dp[j - playScore] : 0;
dp[j] = withoutThisPlay + withThisPlay;
}
}
return dp[finalScore];
}
Arithmetic Slices
A sequence of numbers is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.
For example, these are arithmetic sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not arithmetic.
1, 1, 2, 5, 7
Example:
A = [1, 2, 3, 4]
return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.
The number of new arithmetic slices added will be 1 + dp[i−1] as discussed in the last approach. The sum is also updated by the same count to reflect the new arithmetic slices added.
public int numberOfArithmeticSlices(int[] A) {
int[] dp = new int[A.length];
int sum = 0;
for (int i = 2; i < dp.length; i++) {
if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {
dp[i] = 1 + dp[i - 1]; // all possible sequences
sum += dp[i];
}
}
return sum;
}
// We can also just use one variable and update sum at the very end,
public int numberOfArithmeticSlices2(int[] A) {
int count = 0, sum = 0;
for (int i = 2; i < A.length; i++) {
if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {
count++;
} else {
sum += (count + 1) * (count) / 2;
count = 0;
}
}
return sum += count * (count + 1) / 2;
}
Arithmetic Slices II
A subsequence slice (P0, P1, …, Pk) of sorted array A is called arithmetic if the sequence A[P0], A[P1], …, A[Pk-1], A[Pk] is arithmetic. In particular, this means that k ≥ 2.
Example:
Input: [2, 4, 6, 8, 10]
Output: 7
Explanation:
All arithmetic subsequence slices are:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
To calculate the subsequence slices, we can append a new element A[i] to existing arithmetic subsequences to form new subsequences only if the difference between the sequence’s last element and A[i] is equal to the sequence’s common difference. Thus, we can define the state transitions as:
for all j < i, f[i][A[i] - A[j]] += f[j][A[i] - A[j]] + 1.
As the graph shows: For the forth element 3, if we append it to some arithmetic subsequences ending with 2, these subsequences must have a common difference of 3 - 2 = 1. Indeed there are two: [1, 2] and [1, 2]. So we can append 3 to the end of these subsequences, and the answer is added by 2. Similar to above, it can form new weak arithmetic subsequences [1, 3], [1, 3] and [2, 3].
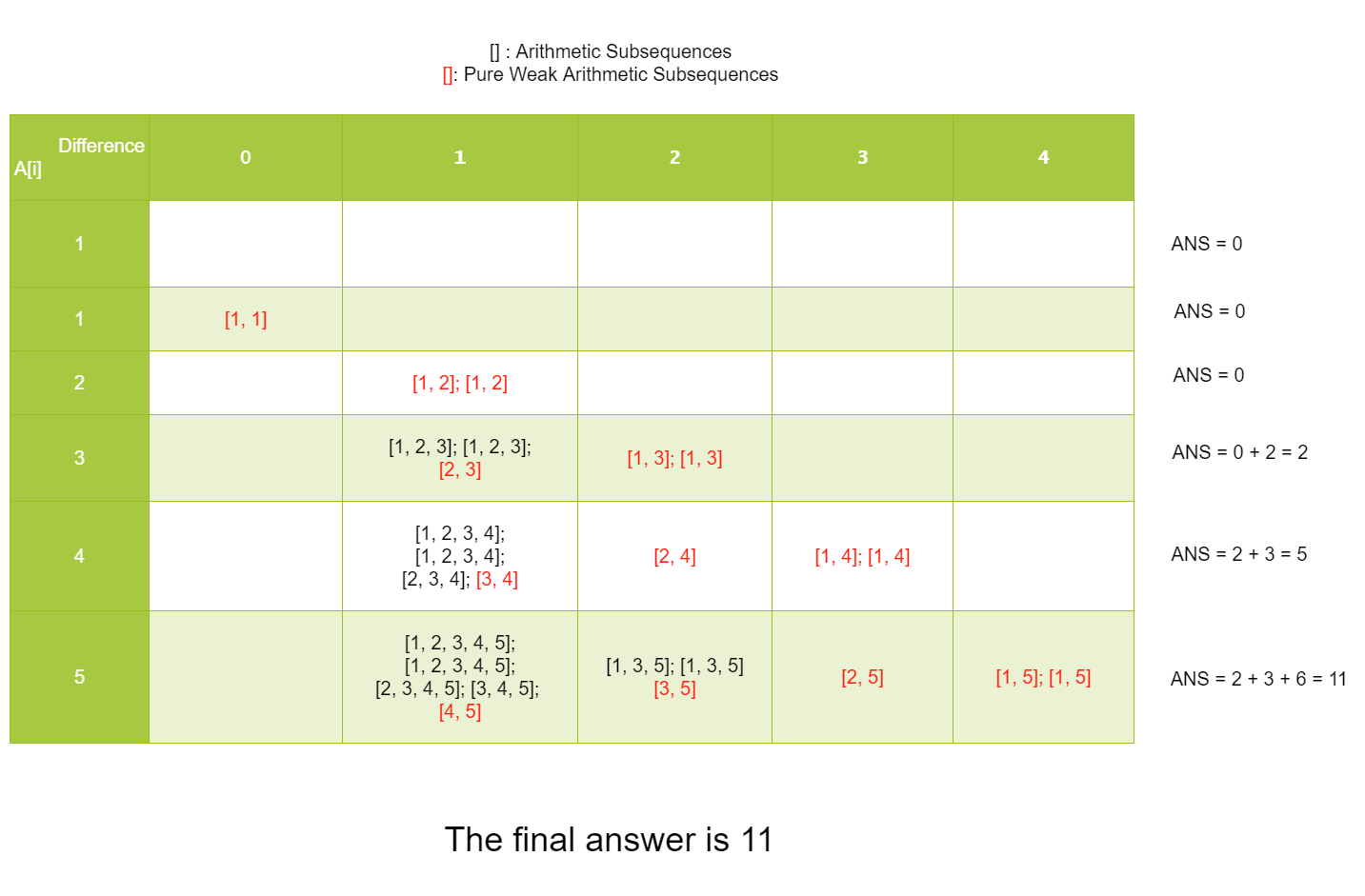
public int numberOfArithmeticSlicesII(int[] A) {
int n = A.length;
long ans = 0;
List<Map<Integer, Integer>> counts = new ArrayList<>();
for (int i = 0; i < n; i++) {
counts.add(new HashMap<>(i));
// attempt to append i to each j
for (int j = 0; j < i; j++) {
long delta = (long) A[i] - (long) A[j];
if (delta < Integer.MIN_VALUE || delta > Integer.MAX_VALUE) {
continue;
}
int diff = (int) delta;
// previous found subsequences till to j
int sum = counts.get(j).getOrDefault(diff, 0);
// count weak subsequences
int origin = counts.get(i).getOrDefault(diff, 0);
// cache all new subsequences (include weak ones)
counts.get(i).put(diff, origin + sum + 1);
ans += sum;
}
}
return (int) ans;
}
Longest Arithmetic Subsequence
/**
* Given an integer array nums and an integer difference, return the length of the longest
* subsequence in nums which is an arithmetic sequence such that the difference between adjacent
* elements in the subsequence equals difference.
*
* Solution:
*
* Traverse from the right of the array and consider it as the starting element of the AP. Determine
* if the nextElement of the AP is present in the Map or not. If No then put the currElement into
* the Map and mark the length of AP considering currElement as the starting point as 1. Else if the
* next element is present in the Map the update the length of the AP considering currElem as
* starting point.
*
*/
public int longestSubsequence(int[] nums, int diff) {
int n = nums.length;
HashMap<Integer, Integer> map = new HashMap<>();
map.put(nums[n - 1], 1);
// dp[i] represents the length of the AP Sequence.
int[] dp = new int[n];
dp[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
int next = nums[i] + diff;
dp[i] = 1 + map.getOrDefault(next, 0);
map.put(nums[i], dp[i]);
}
int ans = 0;
for (int i : dp) {
ans = Math.max(ans, i);
}
return ans;
}
Longest Arithmetic Subsequence Length
/**
* Given an array nums of integers, return the length of the longest arithmetic subsequence (not
* have to be adjacent) in nums.
*
* Example:
*
* Input: nums = [20,1,15,3,10,5,8]
* Output: 4
* Explanation: The longest arithmetic subsequence is [20,15,10,5].
*/
public int longestArithSeqLength(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
// Up to previous num's diff->length map
Map<Integer, Map<Integer, Integer>> map = new HashMap<>();
int ans = 1;
for (int num : nums) {
Map<Integer, Integer> subMap = new HashMap<>();
for (Map.Entry<Integer, Map<Integer, Integer>> entry : map.entrySet()) {
int prevNum = entry.getKey();
int delta = num - prevNum;
int len = 1 + entry.getValue().getOrDefault(delta, 1);
ans = Math.max(ans, len);
subMap.put(delta, len);
}
if (!map.containsKey(num)) {
map.put(num, new HashMap<>());
}
map.get(num).putAll(subMap);
}
return ans;
}
Range Sum Query 2D
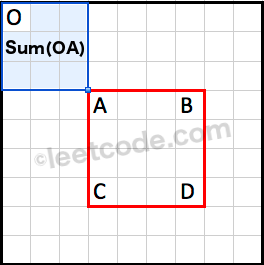
Given a 2D matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Since we might do multiple times of range sum query against this matrix, so we can pre-compute cumulative region sum in matrix. The formular is: Sum(ABCD) = Sum(OD) − Sum(OB) − Sum(OC) + Sum(OA)
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
public class RangeSumQuery2D {
private int[][] dp;
public RangeSumQuery2D(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0)
return;
dp = new int[matrix.length + 1][matrix[0].length + 1];
for (int r = 0; r < matrix.length; r++) {
for (int c = 0; c < matrix[0].length; c++) {
dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
}
}
Range Sum Query 2D - Mutable
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
The colSums = [
[0, 0, 0, 0, 0],
[3, 0, 1, 4, 2],
[8, 6, 4, 6, 3],
[9, 8, 4, 7, 8],
[13, 9, 4, 8, 15],
[14, 9, 7, 8, 20]
]
class NumMatrix {
int[][] matrix;
int[][] colSums;
public NumMatrix(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return;
this.matrix = matrix;
// add one more row in favor of easy coding
this.colSums = new int[matrix.length + 1][matrix[0].length];
for (int r = 1; r < colSums.length; r++) {
for (int c = 0; c < colSums[0].length; c++) {
colSums[r][c] = colSums[r - 1][c] + matrix[r - 1][c];
}
}
}
public void update(int row, int col, int val) {
// just update the bottom rows with the same col
for (int r = row + 1; r < colSums.length; r++) {
colSums[r][col] = colSums[r][col] - matrix[row][col] + val;
}
matrix[row][col] = val;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
for (int c = col1; c <= col2; c++) {
sum += colSums[row2 + 1][c] - colSums[row1][c];
}
return sum;
}
}
Matrix Block Sum
/**
* Given a m x n matrix mat and an integer k, return a matrix answer where each answer[i][j] is the
* sum of all elements mat[r][c] for:
*
* i - k <= r <= i + k, j - k <= c <= j + k, and (r, c) is a valid position in the matrix.
*
*
* Example 1:
*
* Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1 Output: [[12,21,16],[27,45,33],[24,39,28]]
*
* Example 2:
*
* Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2 Output: [[45,45,45],[45,45,45],[45,45,45]]
*
* Solution:
*
* For each row, use a sliding window of size 2 * k to keep the sum updated.
*
* After finishing each row, do it for each columns.
*
* <pre>
* 1 2 3
* 4 5 6
* 7 8 9
* 3 6 5
* 9 15 11
* 15 24 17
* 12 21 16
* 27 45 33
* 24 39 28
* </pre>
*/
public class MatrixBlockSum {
public int[][] matrixBlockSum(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
int[][] tmp = new int[m][n];
int[][] ans = new int[m][n];
for (int i = 0; i < m; i++) {
int sum = 0;
for (int j = 0; j < n + k; j++) {
// minus left num
if (j > 2 * k) {
sum -= mat[i][j - 2 * k - 1];
}
// add right num
if (j < n) {
sum += mat[i][j];
}
// cach the sum
if (j >= k) {
tmp[i][j - k] = sum;
}
}
}
for (int j = 0; j < n; j++) {
int sum = 0;
for (int i = 0; i < m + k; i++) {
if (i > 2 * k) {
sum -= tmp[i - 2 * k - 1][j];
}
if (i < m) {
sum += tmp[i][j];
}
if (i >= k) {
ans[i - k][j] = sum;
}
}
}
return ans;
}
}
Maximal Square
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 4.
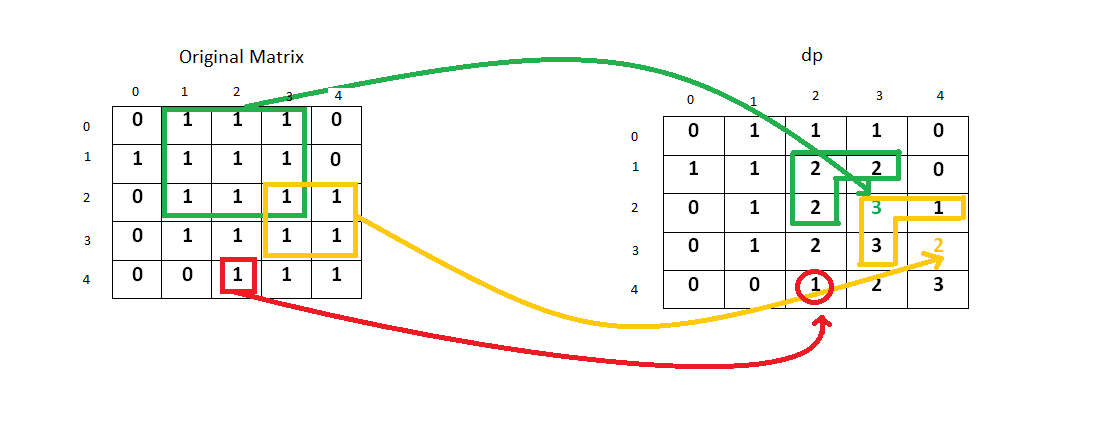
dp(i, j) = min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1.
public int maximalSquare(char[][] matrix) {
int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
int[][] dp = new int[rows + 1][cols + 1];
int maxLen = 0;
// starts with 1 instead of 0 in favor of coding
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
if (matrix[i - 1][j - 1] == '1') {
dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
maxLen = Math.max(maxLen, dp[i][j]);
}
}
}
return maxLen * maxLen;
}
// we can also use 1D array with the equation: dp[j] = min(dp[j−1],dp[j],prev)
public int maximalSquare2(char[][] matrix) {
int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
int[] dp = new int[cols + 1];
int prev = 0, maxLen = 0;
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
int temp = dp[j];
if (matrix[i - 1][j - 1] == '1') {
dp[j] = Math.min(Math.min(prev, dp[j - 1]), dp[j]) + 1;
maxLen = Math.max(maxLen, dp[j]);
} else {
dp[j] = 0;
}
prev = temp;
}
}
return maxLen * maxLen;
}
Maximal Rectangle
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 6.
We can apply the maximum in histogram in each row of the 2D matrix. What we need is to maintain an int array for each row, which represent for the height of the histogram.
public int maximalRectangle(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
int[] heights = new int[matrix[0].length];
int maxArea = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] == '1')
heights[j] += 1; // Add on continous column height
else
heights[j] = 0; // Reset broken column height
}
maxArea = Math.max(maxArea, maxAreaInLine(heights));
}
return maxArea;
}
private int maxAreaInLine(int[] heights) {
Stack<Integer> stack = new Stack<>();
int maxArea = 0;
for (int i = 0; i <= heights.length; i++) {
// Last zero to clear up stack
int height = i == heights.length ? 0 : heights[i];
if (stack.isEmpty() || height >= heights[stack.peek()]) {
stack.push(i);
} else {
int tp = stack.pop();
maxArea = Math.max(maxArea, heights[tp] * (stack.isEmpty() ? i : i - 1 - stack.peek()));
i--; // Keep trying until stack has no more lower height!
}
}
return maxArea;
}
Count Unique BSTs
Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?
Example:
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
Solution: For example, F(3, 7): Construct unique BSTs out of the entire sequence [1, 2, 3, 4, 5, 6, 7] with 3 as the root, which is to say, we need to construct an unique BST out of its left subsequence [1, 2] and another BST out of the right subsequence [4, 5, 6, 7], and then combine them together (i.e. cartesian product). Consider the number of unique BST out of sequence [1, 2] as G(2), and the number of of unique BST out of sequence [4, 5, 6, 7] as G(4). Therefore, F(3, 7) = G(3 - 1) * G(7 - 3) = G(2) * G(4).
Notes: The two sequences [1, 2, 3, 4] and [4, 5, 6, 7] have the same number of unique BSTs.
public int numTrees(int n) {
if (n < 1)
return 0;
// The number of unique BSTs for the ith sequence
int[] dp = new int[n + 1];
// Base cases: n == 0 (empty tree) or n == 1 (only a root)
dp[0] = dp[1] = 1;
// F(i, n) = G(i-1) * G(n-i) 1 <= i <= n
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
Unique Paths In Grid
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below). The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below). How many possible unique paths are there?
public int findHowManyUniquePathsInGrid(int m, int n) {
int[] dp = new int[n];
dp[0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] += dp[j - 1];
}
}
return dp[n - 1];
}
Use traditional 2 dimensional array
public int findHowManyUniquePathsInGrid2(int m, int n) {
int[][] grid = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0)
grid[i][j] = 1;
else
grid[i][j] = grid[i - 1][j] + grid[i][j - 1];
}
}
return grid[m - 1][n - 1];
}
Unique Paths in Obstacle Grid
Now consider if some obstacles are added to the grids. How many unique paths would there be? An obstacle and empty space is marked as 1 and 0 respectively in the grid.
public int findHowManyUniquePathsInGridWithObstacles(int[][] obstacleGrid) {
int width = obstacleGrid[0].length;
int[] dp = new int[width];
dp[0] = 1;
for (int[] row : obstacleGrid) {
for (int j = 0; j < width; j++) {
if (row[j] == 1)
dp[j] = 0;
else if (j > 0)
dp[j] += dp[j - 1];
}
}
return dp[width - 1];
}
Unique Paths III
/**
* You are given an m x n integer array grid where grid[i][j] could be:
*
* <pre>
1 representing the starting square. There is exactly one starting square.
2 representing the ending square. There is exactly one ending square.
0 representing empty squares we can walk over.
-1 representing obstacles that we cannot walk over.
* </pre>
*
* Return the number of 4-directional walks from the starting square to the ending square, that walk
* over every non-obstacle square exactly once.
*/
public int uniquePathsIII(int[][] grid) {
AtomicInteger count = new AtomicInteger(0);
int remain = 0, startRow = 0, startCol = 0;
// Find the start cell
for (int row = 0; row < grid.length; ++row)
for (int col = 0; col < grid[0].length; ++col) {
int cell = grid[row][col];
if (cell >= 0)
remain += 1;
if (cell == 1) {
startRow = row;
startCol = col;
}
}
backtrack(grid, startRow, startCol, remain, count);
return count.get();
}
protected void backtrack(int[][] grid, int row, int col, int remain, AtomicInteger pathCount) {
if (grid[row][col] == 2 && remain == 1) {
pathCount.addAndGet(1); // Reached the destination
return;
}
int temp = grid[row][col];
grid[row][col] = -4; // Visited
remain -= 1; // One less square to visit
int[][] dirs = { { -1, 0 }, { 0, 1 }, { 1, 0, }, { 0, -1 } };
for (int[] dir : dirs) {
int i = row + dir[0];
int j = col + dir[1];
if (0 > i || i >= grid.length || 0 > j || j >= grid[row].length || grid[i][j] < 0)
continue;
backtrack(grid, i, j, remain, pathCount);
}
grid[row][col] = temp;
}
Out of Boundary Paths
There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
Example:
Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
int M = 1000000007;
public int findHowManyOutOfBoundaryPaths(int m, int n, int N, int i, int j) {
int[][][] memo = new int[m][n][N];
for (int[][] a : memo) {
for (int[] b : a) {
Arrays.fill(b, -1);
}
}
return findHowManyOutOfBoundaryPaths(m, n, N, i, j, memo);
}
public int findHowManyOutOfBoundaryPaths(int m, int n, int N, int i, int j, int[][][] memo) {
if (i == m || j == n || i < 0 || j < 0)
return 1;
if (N == 0)
return 0;
if (memo[i][j][N] >= 0)
return memo[i][j][N];
memo[i][j][N] = findHowManyOutOfBoundaryPaths(m, n, N - 1, i - 1, j, memo);
memo[i][j][N] = (memo[i][j][N] + findHowManyOutOfBoundaryPaths(m, n, N - 1, i + 1, j, memo)) % M;
memo[i][j][N] = (memo[i][j][N] + findHowManyOutOfBoundaryPaths(m, n, N - 1, i, j - 1, memo)) % M;
memo[i][j][N] = (memo[i][j][N] + findHowManyOutOfBoundaryPaths(m, n, N - 1, i, j + 1, memo)) % M;
return memo[i][j][N];
}
Find One Path In Grid
Design an algorithm to find a path in a Maze/Grid.
Cache the visited points and use bottom-up programming
public List<Point> findOnePathInGrid(boolean[][] maze) {
if (maze == null || maze.length == 0)
return null;
List<Point> path = new ArrayList<>();
Set<Point> visitedPoints = new HashSet<>();
if (findOnePathInGrid(maze, maze.length - 1, maze[0].length - 1, path, visitedPoints))
return path;
return null;
}
private boolean findOnePathInGrid(boolean[][] maze, int row, int col, List<Point> path, Set<Point> visitedPoints) {
if (col < 0 || row < 0 || !maze[row][col]) // Out of bounds or not available
return false;
Point p = new Point(row, col);
if (visitedPoints.contains(p)) // Already visited this cell
return false;
boolean isAtOrigin = (row == 0) && (col == 0);
// If there's a path from the start to my current location, add my location.
if (isAtOrigin || findOnePathInGrid(maze, row, col - 1, path, visitedPoints)
|| findOnePathInGrid(maze, row - 1, col, path, visitedPoints)) {
path.add(p);
return true;
}
visitedPoints.add(p); // Cache result
return false;
}
Has A Path In Maze?
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction. Given the ball’s start position, the destination and the maze, determine whether the ball could stop at the destination. The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
Example 1 Input 1: a maze represented by a 2D array 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 Input 2: start coordinate (rowStart, colStart) = (0, 4) Input 3: destination coordinate (rowDest, colDest) = (4, 4) Output: true Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Use breadth-first search with caching the visited cells. Use pathTo to track this path and read back to a Stack to return this path.
public boolean hasPathInMaze(int[][] maze, int[] start, int[] destination) {
if (start[0] == destination[0] && start[1] == destination[1])
return true;
int m = maze.length, n = maze[0].length;
int[][] dirs = new int[][] { { -1, 0 }, { 0, 1 }, { 1, 0 }, { 0, -1 } };
boolean[][] visited = new boolean[m][n];
// Use pathTo if we need to track a path!
// int[] pathTo = new int[m * n];
Queue<int[]> queue = new LinkedList<>();
visited[start[0]][start[1]] = true;
queue.offer(start);
while (!queue.isEmpty()) {
int[] p = queue.poll();
for (int[] dir : dirs) {
int x = p[0], y = p[1];
// keep rolling on this direction until hit a wall!
while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0) {
x += dir[0];
y += dir[1];
}
// back to empty space
x -= dir[0];
y -= dir[1];
if (visited[x][y])
continue;
if (x == destination[0] && y == destination[1])
return true;
queue.offer(new int[] { x, y });
visited[x][y] = true;
// pathTo[x * n + y] = p[0] * n + p[1];
}
}
return false;
}
Shortest Distance In Maze
Find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.
Use Dijkstra Algorithm with PriorityQueue to track which is the unvisited node at the shortest distance from the start node.
Time complexity: O(mn*log(mn)); Space complexity: O(mn)
public int shortestDistance(int[][] maze, int[] start, int[] destination) {
int m = maze.length, n = maze[0].length;
int[][] lens = new int[m][n];
for (int i = 0; i < m * n; i++)
lens[i / n][i % n] = Integer.MAX_VALUE;
int[][] dirs = new int[][] { { -1, 0 }, { 0, 1 }, { 1, 0 }, { 0, -1 } };
Queue<int[]> queue = new PriorityQueue<>((a, b) -> (a[2] - b[2]));
queue.offer(new int[] { start[0], start[1], 0 });
while (!queue.isEmpty()) {
int[] p = queue.poll();
if (lens[p[0]][p[1]] <= p[2]) // Already found shorter route
continue;
lens[p[0]][p[1]] = p[2];
for (int[] dir : dirs) {
int x = p[0], y = p[1], l = p[2];
while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0) {
x += dir[0];
y += dir[1];
l++;
}
// Retreat an overstepped one
x -= dir[0];
y -= dir[1];
l--;
if (l < lens[x][y]) {
queue.offer(new int[] { x, y, l });
}
}
}
return lens[destination[0]][destination[1]] == Integer.MAX_VALUE ? -1 : lens[destination[0]][destination[1]];
}
Shortest Distance in Maze III
Find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return “impossible”.
If there is a way for the ball to drop in the hole, the answer instructions should contain the characters ‘u’ (i.e., up), ‘d’ (i.e., down), ‘l’ (i.e., left), and ‘r’ (i.e., right).
Use Dijkstra Algorithm with PriorityQueue to track which is the unvisited node at the shortest distance from the start node.
Time complexity: O(mn*log(mn)); Space complexity: O(mn)
class Point implements Comparable<Point> {
int x, y, len;
String path;
public Point(int x, int y, int len, String path) {
this.x = x;
this.y = y;
this.len = len;
this.path = path;
}
public int compareTo(Point p) {
return len == p.len ? path.compareTo(p.path) : len - p.len;
}
}
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
int m = maze.length, n = maze[0].length;
Point[][] points = new Point[m][n];
for (int i = 0; i < m * n; i++)
points[i / n][i % n] = new Point(i / n, i % n, Integer.MAX_VALUE, "");
int[][] dirs = { { -1, 0 }, { 0, 1 }, { 1, 0, }, { 0, -1 } };
String[] directions = { "u", "r", "d", "l" };
Queue<Point> queue = new PriorityQueue<>(); // using priority queue
queue.offer(new Point(ball[0], ball[1], 0, ""));
while (!queue.isEmpty()) {
Point point = queue.poll();
if (points[point.x][point.y].compareTo(point) <= 0)
continue; // Already found a route shorter
points[point.x][point.y] = point;
for (int i = 0; i < dirs.length; i++) {
int[] dir = dirs[i];
int x = point.x, y = point.y, len = point.len;
while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0 && (x != hole[0] || y != hole[1])) {
x += dir[0];
y += dir[1];
len++;
}
// Retreat an overstepped one
if (x != hole[0] || y != hole[1]) { // Check not in the hole yet
x -= dir[0];
y -= dir[1];
len--;
}
if (len < points[x][y].len) {
queue.offer(new Point(x, y, len, point.path + directions[i]));
}
}
}
return points[hole[0]][hole[1]].len == Integer.MAX_VALUE ? "impossible" : points[hole[0]][hole[1]].path;
}
Robot Room Cleaner
Given a robot cleaner in a room modeled as a grid.
Each cell in the grid can be empty or blocked.
The robot cleaner with 4 given APIs can move forward, turn left or turn right. Each turn it made is 90 degrees.
When it tries to move into a blocked cell, its bumper sensor detects the obstacle and it stays on the current cell.
Design an algorithm to clean the entire room using only the 4 given APIs shown below.
Example:
Input:
room = [
[1,1,1,1,1,0,1,1],
[1,1,1,1,1,0,1,1],
[1,0,1,1,1,1,1,1],
[0,0,0,1,0,0,0,0],
[1,1,1,1,1,1,1,1]
],
row = 1,
col = 3
public void cleanRoom(Robot robot) {
Set<String> visited = new HashSet<>();
// Always clockwise 4 directions: up, right, down, left
int[][] dirs = { { -1, 0 }, { 0, 1 }, { 1, 0 }, { 0, -1 } };
cleanRoomBacktrack(robot, visited, dirs, 0, 0, 0);
}
// Spiral Backtracking, Time Complexity: 4 * (N - M)
public void cleanRoomBacktrack(Robot robot, Set<String> visited, int[][] dirs, int row, int col, int dir) {
robot.clean();
visited.add(row + "," + col);
// Robot can try four directions and pick a not blocked path
for (int i = 0; i < dirs.length; ++i) {
// Use new variables for next cell!!!
int newDir = (dir + i) % 4;
int newRow = row + dirs[newDir][0];
int newCol = col + dirs[newDir][1];
// Check if able to move forward
if (!visited.contains(newRow + "," + newCol) && robot.move()) {
cleanRoomBacktrack(robot, visited, dirs, newRow, newCol, newDir);
// Move back to previous position
robot.turnRight();
robot.turnRight();
robot.move();
robot.turnRight();
robot.turnRight();
}
// Turn to next direction, always match newDir
robot.turnRight();
}
}
Minimum Cost to Hire K Workers
There are N workers. The i-th worker has a quality[i] and a minimum wage expectation wage[i].
Now we want to hire exactly K workers to form a paid group. When hiring a group of K workers, we must pay them according to the following rules:
Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group. Every worker in the paid group must be paid at least their minimum wage expectation. Return the least amount of money needed to form a paid group satisfying the above conditions.
Example 1:
Input: quality = [10,20,5], wage = [70,50,30], K = 2
Output: 105.00000
Explanation: We pay 70 to 0-th worker and 35 to 2-th worker.
Example 2:
Input: quality = [3,1,10,10,1], wage = [4,8,2,2,7], K = 3
Output: 30.66667
Explanation: We pay 4 to 0-th worker, 13.33333 to 2-th and 3-th workers seperately.
Solution:
At least one worker will be paid their minimum wage expectation. If not, we could scale all payments down by some factor and still keep everyone earning more than their wage expectation. For each captain worker that will be paid their minimum wage expectation, let’s calculate the cost of hiring K workers where each point of quality is worth ratio = wage[captain] / quality[captain] dollars.
The key insight is to iterate over the ratio. Let’s say we hire workers with a ratio R or lower. Then, we would want to know the K workers with the lowest quality, and the sum of that quality, the last worker with higher ratio should be paid the min wage. We can use a heap to maintain these variables.
Time Complexity: O(NlogN), where N is the number of workers.
public double mincostToHireWorkers(int[] quality, int[] wage, int K) {
int N = quality.length;
Worker[] workers = new Worker[N];
for (int i = 0; i < N; ++i)
workers[i] = new Worker(quality[i], wage[i]);
// Sort by ratio
Arrays.sort(workers);
double ans = Double.MAX_VALUE;
int sumq = 0;
Queue<Integer> pool = new PriorityQueue<>(Collections.reverseOrder());
for (Worker worker : workers) {
pool.offer(worker.quality);
sumq += worker.quality;
if (pool.size() > K)
sumq -= pool.poll();
if (pool.size() == K)
// all workers in the pool has lower ratio
ans = Math.min(ans, sumq * worker.ratio());
}
return ans;
}
class Worker implements Comparable<Worker> {
public int quality, wage;
public Worker(int q, int w) {
quality = q;
wage = w;
}
public double ratio() {
return (double) wage / quality;
}
public int compareTo(Worker other) {
return Double.compare(ratio(), other.ratio());
}
}
Guess the Word
Example 1: Input: secret = “acckzz”, wordlist = [“acckzz”,”ccbazz”,”eiowzz”,”abcczz”]
Explanation:
master.guess(“aaaaaa”) returns -1, because “aaaaaa” is not in wordlist. master.guess(“acckzz”) returns 6, because “acckzz” is secret and has all 6 matches. master.guess(“ccbazz”) returns 3, because “ccbazz” has 3 matches. master.guess(“eiowzz”) returns 2, because “eiowzz” has 2 matches. master.guess(“abcczz”) returns 4, because “abcczz” has 4 matches.
We made 5 calls to master.guess and one of them was the secret, so we pass the test case.
public void findSecretWord(String[] wordlist, Master master) {
for (int i = 0; i < 10; i++) {
String guess = wordlist[new Random().nextInt(wordlist.length)];
int x = master.guess(guess);
List<String> wordlist2 = new ArrayList<>();
for (String w : wordlist)
if (matchedLetters(guess, w) == x)
wordlist2.add(w);
wordlist = wordlist2.toArray(new String[wordlist2.size()]);
}
}
private int matchedLetters(String a, String b) {
int matches = 0;
for (int i = 0; i < a.length(); ++i)
if (a.charAt(i) == b.charAt(i))
matches++;
return matches;
}
interface Master {
int guess(String word);
}
Bricks Falling When Hit
We have a grid of 1s and 0s; the 1s in a cell represent bricks. A brick will not drop if and only if it is directly connected to the top of the grid, or at least one of its (4-way) adjacent bricks will not drop.
We will do some erasures sequentially. Each time we want to do the erasure at the location (i, j), the brick (if it exists) on that location will disappear, and then some other bricks may drop because of that erasure.
Return an array representing the number of bricks that will drop after each erasure in sequence.
Example 1:
Input:
grid = [[1,0,0,0],[1,1,1,0]]
hits = [[1,0]]
Output: [2]
Explanation:
If we erase the brick at (1, 0), the brick at (1, 1) and (1, 2) will drop. So we should return 2.
private static final int[][] dirs = { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } };
public int[] hitBricks(int[][] grid, int[][] hits) {
int n = grid[0].length;
// remove all hit bricks
for (int i = 0; i < hits.length; i++) {
grid[hits[i][0]][hits[i][1]] -= 1;
}
// dfs from roof, set all cells to 2 so that we know these cells have been visited
for (int c = 0; c < n; c++) {
if (grid[0][c] == 1)
hitBricksDfs(grid, 0, c);
}
int[] ans = new int[hits.length];
// iterate from last hit to first
for (int i = hits.length - 1; i >= 0; i--) {
int r = hits[i][0];
int c = hits[i][1];
grid[r][c] += 1; // put brick back
// if the cell is attathed to the roof (or any cell with value 2)
// count all the connected bricks which fell down when it's hit/cut!
ans[i] = grid[r][c] == 1 && isConnectedTop(grid, r, c) ? hitBricksDfs(grid, r, c) - 1 : 0;
}
return ans;
}
private boolean isConnectedTop(int[][] grid, int r, int c) {
if (r == 0)
return true;
for (int[] dir : dirs) {
int x = r + dir[0], y = c + dir[1];
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length)
continue;
if (grid[x][y] == 2)
return true;
}
return false;
}
private int hitBricksDfs(int[][] grid, int r, int c) {
grid[r][c] = 2;
int size = 1;
for (int[] dir : dirs) {
int x = r + dir[0], y = c + dir[1];
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] != 1)
continue;
size += hitBricksDfs(grid, x, y);
}
return size;
}
Dungeon Game
The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.
Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).
Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.
For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.
-2(K) -3 3
-5 -10 1
10 30 -5(P)
dp[i][j] means minimum HP required to survive from point [i, j] to the end. dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]) if no larger than 0, set to 1
// Recursion
public int calculateMinimumHP(int[][] dungeon) {
return calculate(dungeon, 0, 0, new int[dungeon.length][dungeon[0].length]);
}
public int calculate(int[][] dungeon, int i, int j, int[][] dp) {
if (i >= dungeon.length || j >= dungeon[0].length)
return Integer.MAX_VALUE;
if (dp[i][j] != 0)
return dp[i][j];
// initialization
if (i == dungeon.length - 1 && j == dungeon[0].length - 1)
return dp[i][j] = Math.max(-dungeon[i][j], 0) + 1;
// transition formula
int diff = Math.min(calculate(dungeon, i + 1, j, dp), calculate(dungeon, i, j + 1, dp)) - dungeon[i][j];
// if no larger than 0, set to 1
return dp[i][j] = diff > 0 ? diff : 1;
}
public int calculateMinimumHP2(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int[][] dp = new int[m][n];
dp[m - 1][n - 1] = Math.max(-dungeon[m - 1][n - 1], 0) + 1;
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (i + 1 <= m - 1 && j + 1 <= n - 1) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
} else if (i + 1 <= m - 1) {
dp[i][j] = dp[i + 1][j] - dungeon[i][j];
} else if (j + 1 <= n - 1) {
dp[i][j] = dp[i][j + 1] - dungeon[i][j];
}
if (dp[i][j] <= 0)
dp[i][j] = 1;
}
}
return dp[0][0];
}
4 Keys Keyboard
Imagine you have a special keyboard with the following keys:
Key 1: (A): Print one ‘A’ on screen.
Key 2: (Ctrl-A): Select the whole screen.
Key 3: (Ctrl-C): Copy selection to buffer.
Key 4: (Ctrl-V): Print buffer on screen appending it after what has already been printed.
Now, you can only press the keyboard for N times (with the above four keys), find out the maximum numbers of ‘A’ you can print on screen.
Example 1:
Input: N = 3
Output: 3
Explanation:
We can at most get 3 A's on screen by pressing following key sequence:
A, A, A
Example 2:
Input: N = 7
Output: 9
Explanation:
We can at most get 9 A's on screen by pressing following key sequence:
A, A, A, Ctrl A, Ctrl C, Ctrl V, Ctrl V
Aim : maximum numbers of 'A' after N key presses.
dp[i] : maximum numbers of 'A' after i key presses.
There are 2 possibilities for the last move,
if last move is Adding, dp[i] = dp[i - 1] + 1;
if last move is Multiplying, dp[i] = dp[i - (x + 1)] * x;
If we multiply by 2N, paying a cost of 2N+1, we could instead multiply by N then 2, paying N+4. When N >= 3, we don't pay more by doing it the second way.
Similarly, if we are to multiply by 2N+1 paying 2N+2, we could instead multiply by N+1 then 2, paying N+5. Again, when N >= 3, we don't pay more doing it the second way.
Thus, we never multiply by more than 5.
public int maxA(int N) {
int[] dp = new int[N + 1];
for (int i = 1; i < dp.length; i++) {
dp[i] = dp[i - 1] + 1;
// reserve 2 key presses for Ctrl+A and Ctrl+C
for (int j = 0; j < i - 1; j++) {
dp[i] = Math.max(dp[i], dp[j] * (i - j - 1));
}
}
return dp[N];
}
Longest Consecutive Sequence
Given an unsorted array of integers, find the length of the longest consecutive elements sequence.
For example, Given [100, 4, 200, 1, 3, 2], The longest consecutive elements sequence is [1, 2, 3, 4]. Return its length: 4.
Your algorithm should run in O(n) complexity.
Use a hash set to assist the efficient lookup and comparison.
public int longestConsecutiveSequence(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int num : nums)
set.add(num);
int longestStreak = 1;
for (int num : nums) {
// only check the beginning number of the sequence
if (!set.contains(num - 1)) {
int currentNum = num;
int currentStreak = 1;
// loop until reach the end of the sequence
while (set.contains(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = Math.max(longestStreak, currentStreak);
}
}
return longestStreak;
}
public int longestConsecutive2(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
int maxLength = 0;
for (int num : nums) {
if (!map.containsKey(num)) {
int left = map.getOrDefault(num - 1, 0);
int right = map.getOrDefault(num + 1, 0);
int total = left + right + 1;
maxLength = Math.max(maxLength, total);
map.put(num, total);
// Only need to update head and tail
map.put(num - left, total);
map.put(num + right, total);
}
}
return maxLength;
}
Longest Increasing Sequence
Given an unsorted array of integers, find the number of longest increasing subsequence.
Example 1: Input: [1,3,5,4,7] Output: 2 Explanation: The two longest increasing subsequence are [1, 3, 4, 7] and [1, 3, 5, 7]. Example 2: Input: [2,2,2,2,2] Output: 5 Explanation: The length of longest continuous increasing subsequence is 1, and there are 5 subsequences' length is 1, so output 5.
The idea is to use two arrays len[n] and cnt[n] to record the maximum length of Increasing Subsequence and the corresponding number of these sequence which ends with nums[i], respectively. O(n^2) complexity.
public int longestIncreasingSequence(int[] nums) {
int result = 0, maxLen = 0;
// lengths[i] = length of longest ending in nums[i]
// counts[i] = number of longest ending in nums[i]
int[] lengths = new int[nums.length];
int[] counts = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
lengths[i] = counts[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
// nums[i] can be appended to a longest sequence ending at nums[j].
int newLen = lengths[j] + 1;
if (lengths[i] == newLen)
counts[i] += counts[j];
else if (lengths[i] < newLen) {
lengths[i] = newLen;
counts[i] = counts[j];
}
}
}
if (maxLen == lengths[i])
result += counts[i];
else if (maxLen < lengths[i]) {
maxLen = lengths[i];
result = counts[i];
}
}
return result;
}
We can also use Segment Tree to achieve time complexity O(Nlog(N)) and space complexity O(N). It’s a bit challenging to implement it though :)
public class LongestIncreasingSequences {
public Value merge(Value v1, Value v2) {
if (v1.length == v2.length) {
if (v1.length == 0)
return new Value(0, 1);
return new Value(v1.length, v1.count + v2.count);
}
return v1.length > v2.length ? v1 : v2;
}
public void insert(Node node, int key, Value val) {
if (node.range_left == node.range_right) {
node.val = merge(val, node.val);
return;
} else if (key <= node.getRangeMid()) {
insert(node.getLeft(), key, val);
} else {
insert(node.getRight(), key, val);
}
node.val = merge(node.getLeft().val, node.getRight().val);
}
public Value query(Node node, int key) {
if (node.range_right <= key)
return node.val;
else if (node.range_left > key)
return new Value(0, 1);
else
return merge(query(node.getLeft(), key), query(node.getRight(), key));
}
public int findNumberOfLIS(int[] nums) {
if (nums.length == 0)
return 0;
int min = nums[0], max = nums[0];
for (int num : nums) {
min = Math.min(min, num);
max = Math.max(max, num);
}
Node root = new Node(min, max);
for (int num : nums) {
// query the less neight
Value v = query(root, num - 1);
insert(root, num, new Value(v.length + 1, v.count));
}
return root.val.count;
}
}
class Node {
int range_left, range_right;
Node left, right;
Value val;
public Node(int start, int end) {
range_left = start;
range_right = end;
left = null;
right = null;
val = new Value(0, 1);
}
public int getRangeMid() {
return range_left + (range_right - range_left) / 2;
}
public Node getLeft() {
if (left == null)
left = new Node(range_left, getRangeMid());
return left;
}
public Node getRight() {
if (right == null)
right = new Node(getRangeMid() + 1, range_right);
return right;
}
}
class Value {
int length;
int count;
public Value(int len, int ct) {
length = len;
count = ct;
}
}
Count Palindromic Subsequences
Given a string S, find the number of different non-empty palindromic subsequences in S, and return that number modulo 10^9 + 7.
A subsequence of a string S is obtained by deleting 0 or more characters from S.
A sequence is palindromic if it is equal to the sequence reversed.
Two sequences A_1, A_2, … and B_1, B_2, … are different if there is some i for which A_i != B_i.
Example 1:
Input:
S = 'bccb'
Output: 6
Explanation:
The 6 different non-empty palindromic subsequences are 'b', 'c', 'bb', 'cc', 'bcb', 'bccb'.
Note that 'bcb' is counted only once, even though it occurs twice.
Let dp[x][i][j] be the answer for the substring S[i…j] where S[i] == S[j] == ‘a’+x. Note that since we only have 4 characters a, b, c, d, thus 0 <= x < 4. If S[i] == S[j] == ‘a’+x, then dp[x][i][j] = 2 + dp[0][i+1][j-1] + dp[1][i+1][j-1] + dp[2][i+1][j-1] + dp[3][i+1][j-1]. Time Complexity is O(N^2).
public int countPalindromicSubsequences(String S) {
int n = S.length();
int mod = 1000000007;
int[][][] dp = new int[4][n][n];
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
for (int k = 0; k < 4; k++) {
char c = (char) ('a' + k);
if (i == j) {
dp[k][i][j] = S.charAt(i) == c ? 1 : 0;
} else { // j > i
if (S.charAt(i) != c)
dp[k][i][j] = dp[k][i + 1][j];
else if (S.charAt(j) != c)
dp[k][i][j] = dp[k][i][j - 1];
else {
dp[k][i][j] = 2;
if (j != i + 1) {
for (int m = 0; m < 4; m++) { // count each one within subwindows [i+1][j-1]
dp[k][i][j] += dp[m][i + 1][j - 1];
dp[k][i][j] %= mod;
}
}
}
}
}
}
}
int ans = 0;
for (int k = 0; k < 4; k++) {
ans += dp[k][0][n - 1];
ans %= mod;
}
return ans;
}
Minimum Edit Distance
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
// Bottom Up Recursion
public int minimumEditDistance(String s, String t) {
int[][] distances = new int[s.length()][t.length()];
for (int[] row : distances)
Arrays.fill(row, -1);
return computeEditDistance(s, s.length() - 1, t, t.length() - 1, distances);
}
private int computeEditDistance(String w1, int i, String w2, int j, int[][] distances) {
if (i < 0)
return j + 1; // left of w2
else if (j < 0)
return i + 1; // left of w1
if (distances[i][j] == -1) {
if (w1.charAt(i) == w2.charAt(j)) {
distances[i][j] = computeEditDistance(w1, i - 1, w2, j - 1, distances);
} else {
int insert = computeEditDistance(w1, i, w2, j - 1, distances);
int delete = computeEditDistance(w1, i - 1, w2, j, distances);
int replace = computeEditDistance(w1, i - 1, w2, j - 1, distances);
distances[i][j] = 1 + Math.min(insert, Math.min(delete, replace));
}
}
return distances[i][j];
}
Ones and Zeros
In the computer world, use restricted resource you have to generate maximum benefit is what we always want to pursue.
For now, suppose you are a dominator of m 0s and n 1s respectively. On the other hand, there is an array with strings consisting of only 0s and 1s.
Now your task is to find the maximum number of strings that you can form with given m 0s and n 1s. Each 0 and 1 can be used at most once.
Example 1:
Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4
Explanation: This are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are “10,”0001”,”1”,”0”
/* Using recursion with memoization */
public int findMaxForm(String[] strs, int m, int n) {
int[][][] memo = new int[strs.length][m + 1][n + 1];
return calculate(strs, 0, m, n, memo);
}
private int calculate(String[] strs, int i, int zeroes, int ones, int[][][] memo) {
if (i == strs.length)
return 0;
if (memo[i][zeroes][ones] != 0)
return memo[i][zeroes][ones];
int[] count = countZeroesOnes(strs[i]);
int taken = -1;
if (zeroes - count[0] >= 0 && ones - count[1] >= 0)
taken = calculate(strs, i + 1, zeroes - count[0], ones - count[1], memo) + 1;
int not_token = calculate(strs, i + 1, zeroes, ones, memo);
memo[i][zeroes][ones] = Math.max(taken, not_token);
return memo[i][zeroes][ones];
}
/* Dynamic Programming: dp[i][j] denotes the maximum number of strings that can be included in the subset given only i 0's and j 1's are available. */
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (String s : strs) {
int[] count = countZeroesOnes(s);
for (int zeroes = m; zeroes >= count[0]; zeroes--) {
for (int ones = n; ones >= count[1]; ones--) {
dp[zeroes][ones] = Math.max(1 + dp[zeroes - count[0]][ones - count[1]], dp[zeroes][ones]);
}
}
}
return dp[m][n];
}
private int[] countZeroesOnes(String s) {
int[] count = new int[2];
for (char c : s.toCharArray()) {
count[c - '0']++;
}
return count;
}
Magic Index with Dups
A magic index in an array A[1…n-1] is defined to be an index such that A[i] = i. Given a sorted array of integers those could be not distinct, write a method to find a magic index, if one exists, in array A.
| -10 | 5 | 2 | 2 | 2 | 3 | 4 | 7 | 9 | 12 | 13 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
If the elements are distinct, we can do binary search. When we look at the middle element A[5] = 3, we know that the magic index must be on the right side, since A[mid] < mid.
If the elements are not distinct, when we see that A[mid] < mid, we cannot conclude which side the magic index is on. It could be on either side. Could it be anywhere on the left side? Not exactly. Since A[5] = 3, we know that A[4] couldn’t be a magic index. A[4] would need to be 4 to be the magic index, but A[4] must be less than or equal to A[5]. But we can skip a bunch of elements and only recursively search elements A[0] through A[3]. A[3] is the first element that could be a magic index.
The general pattern is that we compare midIndex and midValue for equality first. Then, if they are not equal, we recursively search the left and right sides as follows:
- Left side: search indices start through Math.min(midIndex - 1, midValue).
- Right side: search indices Math.max(midIndex + 1, midValue) through end.
public int magicIndexWithDups(int[] array) {
return magicIndexWithDups(array, 0, array.length - 1);
}
private int magicIndexWithDups(int[] array, int start, int end) {
if (end < start) {
return -1;
}
int midIndex = start + (end - start) / 2;
int midValue = array[midIndex];
if (midValue == midIndex)
return midIndex;
// Search Left
int leftIndex = Math.min(midIndex - 1, midValue);
int left = magicIndexWithDups(array, 0, leftIndex);
if (left >= 0)
return left;
// Search Right
int rightIndex = Math.max(midIndex + 1, midValue);
int right = magicIndexWithDups(array, rightIndex, end);
return right;
}
Multiply by Using Addition
Write a recursive function to multiply two positive integers without using the * operator (or / operator). You can use addition, subtraction, and bit shifting, but you should minimize the number of those operations.
The logic is that, on even numbers, we just divide smaller by 2 and double the result of the recursive call. On odd numbers, we do the same, but then we also add bigger to this result.
public int multiplyByUsingAddition(int a, int b) {
int smaller = a > b ? b : a;
int bigger = a > b ? a : b;
return minProductRecursive(smaller, bigger);
}
private int minProductRecursive(int smaller, int bigger) {
if (smaller == 0)
return 0;
if (smaller == 1)
return bigger;
int s = smaller >> 1; // Divide by 2
int halfProduct = minProductRecursive(s, bigger);
if ((smaller & 1) == 0)
return halfProduct + halfProduct;
else
return halfProduct + halfProduct + bigger;
}
N Pairs of Parentheses
Implement an algorithm to print all valid (i.e., properly open and closed) combinations of n pairs of parentheses.
Example: Print 3 pairs of parentheses: ((())), (()()), (())(), ()(()), ()()()
We can build the string from scratch. On each recursive call, we have the index for a particular character in the string. We need to select either a left or right paren.
- Left Paren: As long as we haven’t used up all the left parentheses, we can always insert a left paren.
- Right Paren: We can insert a right paren as long as it won’t lead to syntax error: If there are more right parentheses than left.
The number C(k) of strings with k pairs of matched parens grows very rapidly with k. The complexity is O((2k)!/(k!(k+1)!))
public List<String> generateParentheses(int count) {
char[] str = new char[count * 2];
List<String> list = new ArrayList<>();
generateParentheses(list, count, count, str, 0);
return list;
}
private void generateParentheses(List<String> list, int leftRem, int rightRem, char[] str, int index) {
if (leftRem < 0 || rightRem < leftRem)
return; // invalid state
if (leftRem == 0 && rightRem == 0) {
list.add(String.copyValueOf(str));
} else {
str[index] = '('; // Add left and recurse
generateParentheses(list, leftRem - 1, rightRem, str, index + 1);
str[index] = ')'; // Add right and recurse
generateParentheses(list, leftRem, rightRem - 1, str, index + 1);
}
}
Minimum Path Sum In Grid
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
Here, we use a 1D array, and update the array as dp(j) = grid(i,j) + min(dp(j), dp(j+1))
public int minPathSum(int[][] grid) {
int[] dp = new int[grid[0].length];
for (int i = grid.length - 1; i >= 0; i--) {
for (int j = grid[0].length - 1; j >= 0; j--) {
if (i == grid.length - 1 && j != grid[0].length - 1)
dp[j] = grid[i][j] + dp[j + 1];
else if (j == grid[0].length - 1 && i != grid.length - 1)
dp[j] = grid[i][j] + dp[j];
else if (j != grid[0].length - 1 && i != grid.length - 1)
dp[j] = grid[i][j] + Math.min(dp[j], dp[j + 1]);
else
dp[j] = grid[i][j];
}
}
return dp[0];
}
Minimum Total In Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle [ [2], [3,4], [6,5,7], [4,1,8,3] ] The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note: Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
Use ‘Bottom-Up’ DP, the min path sum at the ith node on the kth row would be the lesser one of its two children plus the value of itself. i.e. minLens[k][i] = min(minLens[k+1][i], minLens[k+1][i+1]) + triangle[k][i], or even better to use 1D array. The space complexity is O(n), there are 1+2+…+n=n(n+1)/2 elements, implying an O(n^2) time complexity.
public int minimumTotalInTriangle(List<List<Integer>> triangle) {
int[] minLens = new int[triangle.size() + 1];
for (int layer = triangle.size() - 1; layer >= 0; layer--) {
for (int i = 0; i < triangle.get(layer).size(); i++) {
minLens[i] = Math.min(minLens[i], minLens[i + 1]) + triangle.get(layer).get(i);
}
}
return minLens[0];
}
Champagne Tower

public double champagneTower(int poured, int queryRow, int queryGlass) {
if (queryGlass > queryRow)
return 0.0;
// query glass must in query row
double[][] A = new double[queryRow + 1][queryRow + 1];
A[0][0] = (double) poured;
for (int r = 0; r <= queryRow; r++) {
for (int c = 0; c <= r; c++) {
double q = (A[r][c] - 1.0) / 2.0;
if (q > 0) {
A[r + 1][c] += q;
A[r + 1][c + 1] += q;
}
}
}
return Math.min(1, A[queryRow][queryGlass]);
}
Stack of Boxes
You have a stack of n boxes, with widths, heights and depths. The boxes cannot be rotated and can only be stacked on top of one another if each box in the stack is strictly larger than the box above it in width, height, and depth. Implement a method to compute the height of the tallest possible stack.
If we experimented with each boxes as a bottom and built the biggest stack possible with each, we would find the biggest stack possible. Since it’d be strictly greater, we can sort the boxes on a dimension and we don’t need to look backwards in the list. Plus using memoization.
class Box {
int width, height, depth;
public Box(int width, int height, int depth) {
this.width = width;
this.height = height;
this.depth = depth;
}
public boolean canBeAbove(Box b) {
if (b == null)
return false;
return b.width > width && b.height > height && b.depth > depth;
}
public String toString() {
return "Box(" + width + "," + height + "," + depth + ")";
}
}
public int createStack(List<Box> boxes) {
Collections.sort(boxes, (a, b) -> (b.height - a.height));
int maxHeight = 0;
int[] stackMap = new int[boxes.size()];
for (int i = 0; i < boxes.size(); i++) {
int height = createStack(boxes, i, stackMap);
maxHeight = Math.max(maxHeight, height);
}
return maxHeight;
}
private int createStack(List<Box> boxes, int bottomIndex, int[] stackMap) {
if (bottomIndex < boxes.size() && stackMap[bottomIndex] > 0)
return stackMap[bottomIndex];
Box bottom = boxes.get(bottomIndex);
int maxHeight = 0;
for (int i = bottomIndex + 1; i < boxes.size(); i++) {
if (boxes.get(i).canBeAbove(bottom)) {
int height = createStack(boxes, i, stackMap);
maxHeight = Math.max(height, maxHeight);
}
}
maxHeight += bottom.height;
stackMap[bottomIndex] = maxHeight;
return maxHeight;
}
private int createStack2(List<Box> boxes) {
Collections.sort(boxes, (a, b) -> (b.height - a.height));
int[] stackMap = new int[boxes.size()];
return createStack2(boxes, null, 0, stackMap);
}
private int createStack2(List<Box> boxes, Box bottom, int offset, int[] stackMap) {
if (offset >= boxes.size())
return 0; // Base case
Box newBottom = boxes.get(offset);
int heightWithBottom = 0;
if (bottom == null || newBottom.canBeAbove(bottom)) {
if (stackMap[offset] == 0) {
stackMap[offset] = createStack2(boxes, newBottom, offset + 1, stackMap);
stackMap[offset] += newBottom.height;
}
heightWithBottom = stackMap[offset];
}
int heightWithoutBottom = createStack2(boxes, bottom, offset + 1, stackMap);
return Math.max(heightWithBottom, heightWithoutBottom);
}
N Queens Chessboard
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Whether a queen can be placed here or not, is related to all previous placed queens. Please note columns[row]=col.
public List<List<String>> solveNQueens(int n) {
List<List<String>> boards = new ArrayList<>();
List<int[]> results = new ArrayList<>();
// Store column index for each row
int[] columns = new int[n];
// Initialize column index as -1
Arrays.fill(columns, -1);
placeQueens(0, columns, results);
for (int[] result : results) {
boards.add(drawBoard(result));
}
return boards;
}
public void placeQueens(int row, int[] columns, List<int[]> results) {
if (row == columns.length) {
results.add(columns.clone());
return;
}
// Try to place queue at all possible columns
for (int col = 0; col < columns.length; col++) {
if (checkValid(columns, row, col)) {
columns[row] = col; // Place queue
placeQueens(row + 1, columns, results);
}
}
}
public boolean checkValid(int[] columns, int row1, int col1) {
for (int row2 = 0; row2 < row1; row2++) {
int col2 = columns[row2];
// Check if rows have a queen in the same column
if (col1 == col2)
return false;
// Check diagonals: means they have same distances.
int colDistance = Math.abs(col1 - col2);
int rowDistance = row1 - row2;
if (colDistance == rowDistance)
return false;
}
return true;
}
public List<String> drawBoard(int[] columns) {
List<String> board = new ArrayList<>();
for (int i = 0; i < columns.length; i++) {
char[] row = new char[columns.length];
Arrays.fill(row, '.');
for (int j = 0; j < columns.length; j++) {
if (columns[i] == j) {
row[j] = 'Q';
}
}
board.add(new String(row));
}
return board;
}
Knight on A Keypad
Given a phone keypad as below:
1 2 3
4 5 6
7 8 9
0
Let’s start with 1, and you can only make the movement as the Knight in a chess game. E.g. if we are at 1 then the next digit can be eight 6 or 8, if we are at 6 then the next digit can be 1, 7 or 0.
Repetition of digits are allowed - 1616161616 is a valid number.
The question is how many different 10-digit numbers can be formed starting from 1?
Solution:
It can be done in polynomial time, with the dynamic programming and memoization.
Lets assume N (the number of digits) equals 10 for the example.
Thinking of it recursively like this: How many numbers can I construct using 10 digits starting from 1?
Answer is
[number of 9-digit numbers starting from 8] +
[number of 9-digit numbers starting from 6].
So how many “9-digit numbers starting from 8” are there? Well,
[number of 8-digit numbers starting from 1] +
[number of 8-digit numbers starting from 3]
And so on. Base case is reached when you get the question “How many 1-digit numbers are there starting from X” (and the answer is obviously 1).
The algorithm simply fills the 2D matrix[length][10], and the complexity is O(10*N), runs in linear time.
public class KnightOnKeypad {
// The valid movements from any number 0 through 9!
int[][] nexts = { { 4, 6 }, { 6, 8 }, { 7, 9 }, { 4, 8 }, { 0, 3, 9 }, {}, { 1, 7, 0 }, { 2, 6 }, { 1, 3 }, { 2, 4 } };
// iterative, needs to calculate all digits for each length
public int countIterative(int digit, int length) {
int[][] matrix = new int[length][10];
Arrays.fill(matrix[0], 1);
for (int len = 1; len < length; len++) {
for (int dig = 0; dig <= 9; dig++) {
int sum = 0;
for (int i : nexts[dig]) {
sum += matrix[len - 1][i];
}
matrix[len][dig] = sum;
}
}
return matrix[length - 1][digit];
}
// recursive, DFS, with memorization, just calculate the reached ones.
// Not the length starts from 1 instead of zero
public int countRecursive(int digit, int length, int[][] matrix) {
if (length == 1)
return 1;
// already reached and cached
if (matrix[length - 1][digit] > 0)
return matrix[length - 1][digit];
int sum = 0;
for (int i : nexts[digit]) {
sum += countRecursive(i, length - 1, matrix);
}
matrix[length - 1][digit] = sum;
return sum;
}
// recursive, DFS, with memorization, just calculate the reached ones.
// NOTE: the length is between [1, 10] instead of [0, 9]!
public int countRecursive(int digit, int length, int[][] matrix) {
if (length == 1)
return 1;
// already reached and cached
if (matrix[length - 1][digit] > 0)
return matrix[length - 1][digit];
int sum = 0;
for (int i : nexts[digit]) {
sum += countRecursive(i, length - 1, matrix);
}
matrix[length - 1][digit] = sum;
return sum;
}
// BFS, Top-Down
public void permuteRecursive(int digit, int length, List<String> temp, List<String> results) {
if (length == 0) {
results.addAll(temp);
return;
}
for (int dig : nexts[digit]) {
List<String> list = new ArrayList<>();
for (String number : temp) {
list.add(number + dig);
}
permuteRecursive(dig, length - 1, list, results);
}
}
// BFS, Top-Down
public void permuteRecursive2(int digit, int length, List<String> temp, List<String> results) {
List<String> list = new ArrayList<>();
for (String number : temp) {
list.add(number + digit);
}
length = length - 1;
if (length == 0) {
results.addAll(list);
return;
}
for (int dig : nexts[digit]) {
permuteRecursive2(dig, length, list, results);
}
}
// DFS, Bottom-Up
public List<String> permuteRecursive3(int digit, int length) {
List<String> results = new ArrayList<>();
if (length == 1) {
results.add("" + digit);
return results;
}
for (int dig : nexts[digit]) {
for (String number : permuteRecursive3(dig, length - 1)) {
results.add(digit + number);
}
}
return results;
}
public static void main(String[] args) {
KnightOnKeypad solution = new KnightOnKeypad();
assert solution.countIterative(1, 10) == 1424;
assert solution.countRecursive(1, 10, new int[10][10]) == 1424;
List<String> results = new ArrayList<>();
solution.permuteRecursive(1, 10 - 1, Arrays.asList("1"), results);
assert results.size() == 1424;
results = new ArrayList<>();
solution.permuteRecursive2(1, 10, Arrays.asList(""), results);
assert results.size() == 1424;
results = solution.permuteRecursive3(1, 10);
assert results.size() == 1424;
}
}
Minimum Swaps
We have two integer sequences A and B of the same non-zero length.
We are allowed to swap elements A[i] and B[i]. Note that both elements are in the same index position in their respective sequences.
At the end of some number of swaps, A and B are both strictly increasing. (A sequence is strictly increasing if and only if A[0] < A[1] < A[2] < … < A[A.length - 1].)
Given A and B, return the minimum number of swaps to make both sequences strictly increasing. It is guaranteed that the given input always makes it possible.
Example:
Input: A = [1,3,5,4], B = [1,2,3,7]
Output: 1
Explanation:
Swap A[3] and B[3]. Then the sequences are:
A = [1, 3, 5, 7] and B = [1, 2, 3, 4]
which are both strictly increasing.
swapRecord means for the ith element in A and B, the minimum swaps if we swap A[i] and B[i]; fixRecord means for the ith element in A and B, the minimum swaps if we DONOT swap A[i] and B[i].
public int minSwap(int[] A, int[] B) {
int swapRecord = 1, fixRecord = 0;
for (int i = 1; i < A.length; i++) {
if (A[i - 1] >= B[i] || B[i - 1] >= A[i]) {
// The ith manipulation should be same as the i-1th manipulation fixRecord = fixRecord;
swapRecord++;
} else if (A[i - 1] >= A[i] || B[i - 1] >= B[i]) {
// The ith manipulation should be the opposite of the i-1th manipulation
int temp = swapRecord;
swapRecord = fixRecord + 1;
fixRecord = temp;
} else {
// Either swap or fix is OK. Let's keep the minimum one
int min = Math.min(swapRecord, fixRecord);
swapRecord = min + 1;
fixRecord = min;
}
}
return Math.min(swapRecord, fixRecord);
}
Push Dominoes
There are N dominoes in a line, and we place each domino vertically upright.
In the beginning, we simultaneously push some of the dominoes either to the left or to the right.

Example 1: Input: ".L.R...LR..L.." Output: "LL.RR.LLRRLL.."
// Scanning from left to right, our force decays by 1 every iteration, and resets to N if we meet an
// 'R', so that force[i] is higher (than force[j]) if and only if dominoes[i] is closer (looking
// leftward) to 'R' (than dominoes[j]).
public String pushDominoes(String S) {
int N = S.length();
char[] A = S.toCharArray();
int[] forces = new int[N];
int force = 0;
for (int i = 0; i < N; i++) {
force = A[i] == 'R' ? N : A[i] == 'L' ? 0 : Math.max(force - 1, 0);
forces[i] += force;
}
force = 0;
for (int i = N - 1; i >= 0; i--) {
force = A[i] == 'L' ? N : A[i] == 'R' ? 0 : Math.max(force - 1, 0);
forces[i] -= force;
}
StringBuilder ans = new StringBuilder();
for (int f : forces) {
ans.append(f > 0 ? 'R' : f < 0 ? 'L' : '.');
}
return ans.toString();
}
Interleaving String
Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
Example 1: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" Output: true Example 2: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" Output: false
To implement this method, we’ll make use of a 2-d boolean array dp. In this array dp[i][j] implies if it is possible to obtain a substring of length (i+j+2) which is a prefix of s3 by some interleaving of prefixes of strings s1 and s2 having lengths (i+1) and (j+1) respectively.
// DFS is the most efficient way!
public boolean isInterleave(String s1, String s2, String s3) {
if (s1.length() + s2.length() != s3.length())
return false;
return dfs(s1, s2, s3, 0, 0, 0, new boolean[s1.length() + 1][s2.length() + 1]);
}
public boolean dfs(String s1, String s2, String s3, int i, int j, int k, boolean[][] invalid) {
if (invalid[i][j])
return false;
if (k == s3.length())
return true;
boolean valid = (i < s1.length() && s1.charAt(i) == s3.charAt(k) && dfs(s1, s2, s3, i + 1, j, k + 1, invalid))
|| (j < s2.length() && s2.charAt(j) == s3.charAt(k) && dfs(s1, s2, s3, i, j + 1, k + 1, invalid));
if (!valid)
invalid[i][j] = true;
return valid;
}
// DP has the stable complexity O(m*n)
public boolean isInterleave2(String s1, String s2, String s3) {
if (s3.length() != s1.length() + s2.length())
return false;
boolean dp[][] = new boolean[s1.length() + 1][s2.length() + 1];
dp[0][0] = true;
for (int i = 1; i < dp.length; i++)
dp[i][0] = dp[i - 1][0] && s1.charAt(i - 1) == s3.charAt(i - 1);
for (int j = 1; j < dp[0].length; j++)
dp[0][j] = dp[0][j - 1] && s2.charAt(j - 1) == s3.charAt(j - 1);
for (int i = 1; i <= s1.length(); i++) {
for (int j = 1; j <= s2.length(); j++) {
dp[i][j] = (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) || (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
}
}
return dp[s1.length()][s2.length()];
}
Distinct Subsequences
Given a string S and a string T, count the number of distinct subsequences of S which equals T.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ACE” is a subsequence of “ABCDE” while “AEC” is not).
Example 1:
Input: S = "rabbbit", T = "rabbit" Output: 3 Explanation: As shown below, there are 3 ways you can generate "rabbit" from S. (The caret symbol ^ means the chosen letters) rabbbit ^^^^ ^^ rabbbit ^^ ^^^^ rabbbit ^^^ ^^^
public int numDistinct(String s, String t) {
if (s == null || t == null)
return 0;
int[][] dp = new int[s.length() + 1][t.length() + 1];
// if both t and s are ""
dp[0][0] = 1;
// always 1 if t is "" and s can be any char
for (int i = 1; i < dp.length; i++)
dp[i][0] = 1;
// always 0 if s is "" and t can be any char
for (int j = 1; j < dp[0].length; j++)
dp[0][j] = 0;
// main process goes here!
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
// carry forward previous number
dp[i][j] = dp[i - 1][j];
if (s.charAt(i - 1) == t.charAt(j - 1))
// increase when also match
dp[i][j] += dp[i - 1][j - 1];
}
}
return dp[s.length()][t.length()];
}
Backtrack Boot Camp
Backtrack is a general recursive algorithm, tries to build a solution to a computational problem incrementally.
Enumerate in Order
public List<String> enumerate(List<List<Object>> listOfLists) {
List<String> results = new ArrayList<>();
if (listOfLists.size() == 0)
return results;
results.add(new String());
for (List<Object> list : listOfLists) {
List<String> temp = new ArrayList<>();
for (String result : results) {
for (Object obj : list) {
temp.add(result + obj);
}
}
results = temp;
}
return results;
}
public static void main(String[] args) {
BacktrackBootCamp solution = new BacktrackBootCamp();
List<List<Object>> listOfLists = new ArrayList<>();
listOfLists.add(Arrays.asList("a", "b", "c", "d"));
listOfLists.add(Arrays.asList(1, 2, 3, 4, 5));
listOfLists.add(Arrays.asList("Tom", "Mike", "Joe"));
List<StringBuilder> results = solution.enumerate(listOfLists);
for (StringBuilder builder : results) {
System.out.println(builder.toString());
}
}
Compute Power Set
Given a set of distinct integers, nums, return all possible subsets. also called the Powerset P(n). Note: The solution set must not contain duplicate subsets.
For example, If nums = [1,2,3], a solution is: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
When we generate a subset, each element can be either being chosen or not. The best case time is actually the total number of elements across all of the subsets. The solutions will be roughly \(O(n*2^{n-1})\) in space or time complexity.
The subsets of \({a_1, a_2, ..., a_n}\) are also called the P(n). Generating P(n) for the general case is just a simple generalization of the above steps. We compute P(n-1), clone the results, and then add \(a_n\) to each of these cloned sets.
// Simply use iteration
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> allSubsets = new ArrayList<>();
allSubsets.add(new ArrayList<>());
for (int i = 0; i < nums.length; i++) {
List<List<Integer>> moreSubsets = new ArrayList<>();
int item = nums[i];
for (List<Integer> subset : allSubsets) {
List<Integer> newSubset = new ArrayList<>(subset);
newSubset.add(item);
moreSubsets.add(newSubset);
}
allSubsets.addAll(moreSubsets);
}
return allSubsets;
}
// Use backtrack or replicate recursive
public List<List<Integer>> subsets2(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> temp, int[] nums, int start) {
list.add(new ArrayList<>(temp));
for (int i = start; i < nums.length; i++) {
temp.add(nums[i]);
backtrack(list, temp, nums, i + 1);
temp.remove(temp.size() - 1);
}
}
Subsets with K Size
There are a number of testing applications in which it’s required to compute all subsets of a given size for a specified set.
Complexity: \({n \choose k} = {1 \over k!} * {n! \over (n - k)!} = {n! \over k!(n - k)!}\)
public List<List<Integer>> subsetsK(int[] nums, int k) {
List<List<Integer>> list = new ArrayList<>();
backtrackK(list, new ArrayList<>(), nums, 0, k);
return list;
}
private void backtrackK(List<List<Integer>> list, List<Integer> temp, int[] nums, int start, int k) {
if (temp.size() == k) {
list.add(new ArrayList<>(temp));
} else {
int numRemaining = k - temp.size();
// Just skip if not enough nums left!
for (int i = start; i < nums.length && numRemaining <= nums.length - i; i++) {
temp.add(nums[i]);
backtrackK(list, temp, nums, i + 1, k);
temp.remove(temp.size() - 1);
}
}
}
Subsets With Duplicates
Given a collection of integers that might contain duplicates, nums, return all possible subsets.
Make sure we sort the nums first, then check to skip duplicates.
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrackWithDup(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrackWithDup(List<List<Integer>> list, List<Integer> tempList, int[] nums, int start) {
list.add(new ArrayList<>(tempList));
for (int i = start; i < nums.length; i++) {
if (i > start && nums[i] == nums[i - 1])
continue; // skip duplicates
tempList.add(nums[i]);
backtrack(list, tempList, nums, i + 1);
tempList.remove(tempList.size() - 1);
}
}
Compute Permutations
Given a collection of distinct numbers, return all possible unique permutations.
For example, [1,2,3] have the following permutations: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
The time complexity is O(n*n!); The space complexity is O(n); The space to hold the results is O(n*n!)
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
backtrack(result, new ArrayList<>(), nums, new boolean[nums.length]);
return result;
}
private void backtrack(List<List<Integer>> results, List<Integer> temp, int[] nums, boolean[] used) {
if (temp.size() == nums.length) {
results.add(new ArrayList<>(temp));
} else {
for (int i = 0; i < nums.length; i++) {
// if (temp.contains(nums[i]))
if (used[i])
continue; // element already exists, skip!
used[i] = true;
temp.add(nums[i]);
backtrack(results, temp, nums, used);
used[i] = false;
temp.remove(temp.size() - 1);
}
}
}
// If contains duplicates, e.g. [1,1,2]
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
Arrays.sort(nums); // sort the list first!
backtrack2(results, new ArrayList<>(), nums, new boolean[nums.length]);
return results;
}
private void backtrack2(List<List<Integer>> results, List<Integer> temp, int[] nums, boolean[] used) {
if (temp.size() == nums.length) {
results.add(new ArrayList<>(temp));
} else {
for (int i = 0; i < nums.length; i++) {
// used[i - 1] to bind nums[i] and nums[i - 1] together!
// either use[i - 1] or !use[i - 1] works for this case
if (used[i] || (i > 0 && nums[i] == nums[i - 1] && used[i - 1]))
continue;
used[i] = true;
temp.add(nums[i]);
backtrack2(results, temp, nums, used);
used[i] = false;
temp.remove(temp.size() - 1);
}
}
}
public List<List<Integer>> permuteUnique2(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
Map<Integer, Integer> counts = new HashMap<>();
for (int num : nums) {
counts.put(num, counts.getOrDefault(num, 0) + 1);
}
backtrack3(results, new ArrayList<>(), nums.length, counts);
return results;
}
private void backtrack3(List<List<Integer>> results, List<Integer> temp, int length, Map<Integer, Integer> counts) {
if (temp.size() == length) {
results.add(new ArrayList<>(temp));
} else {
counts.forEach((key, count) ->
{
if (count > 0) {
temp.add(key);
counts.put(key, count - 1);
backtrack3(results, temp, length, counts);
temp.remove(temp.size() - 1);
counts.put(key, count);
}
});
}
}
Permutation Sequence
The set [1,2,3,…,n] contains a total of n! unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for n = 3:
“123” “132” “213” “231” “312” “321” Given n and k, return the kth permutation sequence.
Example 1:
Input: n = 3, k = 3
Output: "213"
Example 2:
Input: n = 4, k = 9
Output: "2314"
public String getPermutation(int n, int k) {
List<Integer> samples = new ArrayList<Integer>();
for (int i = 1; i <= n; i++) {
samples.add(i);
}
return helper(samples, k);
}
public String helper(List<Integer> samples, int k) {
if (samples.size() == 0) {
return "";
}
int size = samples.size();
int product = 1;
int i = 1;
while (i < size) {
product = product * i;
i++;
}
int index = (k - 1) / product;
int remain = k - index * product;
return samples.remove(index) + "" + helper(samples, remain);
}
Combination Sum
Given a set of candidate numbers (C) (without duplicates) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
The same repeated number may be chosen from C unlimited number of times.
Note: All numbers (including target) will be positive integers. The solution set must not contain duplicate combinations.
For example, given candidate set [2, 3, 6, 7] and target 7, A solution set is: [ [7], [2, 2, 3] ]
public List<List<Integer>> combinationSum(int[] nums, int target) {
List<List<Integer>> list = new ArrayList<>();
// Arrays.sort(nums); // sort first in favor of skipping duplicates!
backtrack(list, new ArrayList<>(), nums, target, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> temp, int[] nums, int remain, int start) {
if (remain < 0)
return;
else if (remain == 0)
list.add(new ArrayList<>(temp));
else {
for (int i = start; i < nums.length; i++) {
// if (i > start && nums[i] == nums[i - 1])
// continue; // skip duplicates
temp.add(nums[i]);
// backtrack(list, temp, nums, remain - nums[i], i + 1); // can be only used once!
backtrack(list, temp, nums, remain - nums[i], i); // not i + 1 because we can reuse
// same elements
temp.remove(temp.size() - 1);
}
}
}
Palindrome Partitioning
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
For example, given s = “aab”, Return [ [“aa”,”b”], [“a”,”a”,”b”] ]
public List<List<String>> partition(String s) {
List<List<String>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), s, 0);
return list;
}
public void backtrack(List<List<String>> list, List<String> temp, String s, int start) {
if (start == s.length())
list.add(new ArrayList<>(temp));
else {
for (int i = start; i < s.length(); i++) {
if (isPalindrome(s, start, i)) {
temp.add(s.substring(start, i + 1));
backtrack(list, temp, s, i + 1);
temp.remove(temp.size() - 1);
}
}
}
}
public boolean isPalindrome(String s, int low, int high) {
while (low < high)
if (s.charAt(low++) != s.charAt(high--))
return false;
return true;
}
Palindrome Partition II
Given a string s, partition s such that every substring of the partition is a palindrome.
Return the minimum cuts needed for a palindrome partitioning of s.
Use DP Solution.
public int minCut(String s) {
int n = s.length();
int[] dp = new int[n]; // min cut for s[0:j) to be partitioned
boolean[][] isPal = new boolean[n][n]; // true means s[j:i) is a valid palindrome
for (int i = 0; i < n; i++) {
int min = i;
for (int j = 0; j <= i; j++) {
// [j, i] is palindrome if [j + 1, i - 1] is palindrome and s[j] == s[i]
if (s.charAt(j) == s.charAt(i) && (j + 1 > i - 1 || isPal[j + 1][i - 1])) {
isPal[j][i] = true;
min = j == 0 ? 0 : Math.min(min, dp[j - 1] + 1);
}
}
dp[i] = min;
}
return dp[n - 1];
}
Make a String Palindrome
/**
* Given a string s. In one step you can insert any character at any index of the string.
*
* Return the minimum number of steps to make s palindrome.
*
* A Palindrome String is one that reads the same backward as well as forward.
*
* <pre>
* Example 2:
*
* Input: s = "mbadm"
* Output: 2
* Explanation: String can be "mbdadbm" or "mdbabdm".
* </pre>
*
*/
public class MinimumInsertionToMakePalindrome {
public int minInsertions(String s) {
int n = s.length();
if (n <= 1)
return 0;
return makePalindrome(s, 0, n - 1, new int[n][n]);
}
private int makePalindrome(String s, int i, int j, int[][] dp) {
if (i >= j)
return 0;
if (dp[i][j] > 0)
return dp[i][j];
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = makePalindrome(s, i + 1, j - 1, dp);
} else {
dp[i][j] = 1 + Math.min(makePalindrome(s, i + 1, j, dp), makePalindrome(s, i, j - 1, dp));
}
return dp[i][j];
}
}
Shortest Palindrome
Given a string s, you are allowed to convert it to a palindrome by adding characters in front of it. Find and return the shortest palindrome you can find by performing this transformation.
Example 1:
Input: "aacecaaa"
Output: "aaacecaaa"
Example 2:
Input: "abcd"
Output: "dcbabcd"
Take the string “abcbabcab”. Here, the largest palindrome segment from beginning is “abcba”, and the remaining segment is “bcab”. Hence the required string is reverse of “bcab”(=”bacb”) + original string(=”abcbabcab”) = “bacbabcbabcab”. The complexity is O(n^2)
The second solution is we can use the KMP (Knuth–Morris–Pratt) lookup table generation to achieve O(n) complexity.
public String shortestPalindrome(String s) {
if (s == null || s.length() <= 1)
return s;
String temp = s + "#" + new StringBuilder(s).reverse().toString();
int[] position = new int[temp.length()]; // dpa table
// skip index 0 as we will not match a string with itself
for (int i = 1; i < position.length; i++) {
// compare prefix with current
int prefix = position[i - 1];
while (prefix > 0 && temp.charAt(prefix) != temp.charAt(i))
prefix = position[prefix - 1];
position[i] = prefix + ((temp.charAt(prefix) == temp.charAt(i)) ? 1 : 0);
}
// reverse the remain part and add to the front
return new StringBuilder(s.substring(position[position.length - 1])).reverse().toString() + s;
}
Largest Palindrome Product
Find the largest palindrome made from the product of two n-digit numbers.
Since the result could be very large, you should return the largest palindrome mod 1337.
Example: Input: 2, Output: 987, Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
public int largestPalindrome(int n) {
if (n == 1)
return 9;
int max = (int) Math.pow(10, n) - 1;
for (int v = max - 1; v > max / 10; v--) {
long u = Long.valueOf(v + new StringBuilder().append(v).reverse().toString());
for (long x = max; x * x >= u; x--)
if (u % x == 0)
return (int) (u % 1337);
}
return 0;
}
Coins Questions
Coin Change Combinations
You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.
Example 1: Input: amount = 5, coins = [1, 2, 5] Output: 4 Explanation: there are four ways to make up the amount: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1 Example 2: Input: amount = 3, coins = [2] Output: 0 Explanation: the amount of 3 cannot be made up just with coins of 2. Example 3: Input: amount = 10, coins = [10] Output: 1
// dp[i][j]: the number of combinations to make up amount j by using the first i types of coins.
// dp[i][j] only rely on dp[i-1][j] and dp[i][j-coins[i]], we can just using one-dimension array.
public int coinChangeCombinations(int[] coins, int amount) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = 1; i <= amount; i++) {
if (i >= coin)
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
Coin Change Fewest Coins
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
Example 1: coins = [1, 2, 5], amount = 11 return 3 (11 = 5 + 5 + 1) Example 2: coins = [2], amount = 3 return -1.
public int coinChangeFewestCoins(int[] coins, int amount) {
if (amount < 1)
return 0;
return coinChangeFewestCoins(coins, amount, new int[amount + 1]);
}
private int coinChangeFewestCoins(int[] coins, int remain, int[] counts) {
if (remain < 0)
return -1;
if (remain == 0)
return 0;
if (counts[remain] != 0)
return counts[remain];
int min = Integer.MAX_VALUE;
for (int coin : coins) {
int count = coinChangeFewestCoins(coins, remain - coin, counts);
if (count >= 0)
min = Math.min(min, count + 1);
}
counts[remain] = (min == Integer.MAX_VALUE) ? -1 : min;
return counts[remain];
}
public int coinChangeFewestCoins2(int[] coins, int amount) {
if (amount < 1)
return 0;
int[] dp = new int[amount + 1];
int sum = 0;
while (++sum <= amount) {
int min = -1;
for (int coin : coins) {
if (sum >= coin && dp[sum - coin] != -1) {
int temp = dp[sum - coin] + 1;
min = min < 0 ? temp : (temp < min ? temp : min);
}
}
dp[sum] = min;
}
return dp[amount];
}
Pick Up Coins For Maximum Gain
Pick up coins for maximum gain. Two players take turns at choosing one coin each, they can only choose from the 2 ends.
For every pick up, Each player is trying to minimize the other’s revenue.
public static int pickUpCoins(List<Integer> coins) {
return computeMaximum(coins, 0, coins.size() - 1, new int[coins.size()][coins.size()]);
}
private static int computeMaximum(List<Integer> coins, int a, int b, int[][] maximumRevenue) {
if (a > b) {
// No coins left.
return 0;
}
if (maximumRevenue[a][b] == 0) {
// A picked one from the left side first, B will try to pick from the side
// which can minimize A's total revenue. So when B picked from left side,
// A's next pick will be either a+2 or b; when B picked from right side,
// A's next pick will be either a+1, b-1.
int maximumRevenueA = coins.get(a) + Math.min(computeMaximum(coins, a + 2, b, maximumRevenue),
computeMaximum(coins, a + 1, b - 1, maximumRevenue));
// Now consider B pick up first
int maximumRevenueB = coins.get(b) + Math.min(computeMaximum(coins, a + 1, b - 1, maximumRevenue),
computeMaximum(coins, a, b - 2, maximumRevenue));
maximumRevenue[a][b] = Math.max(maximumRevenueA, maximumRevenueB);
}
return maximumRevenue[a][b];
}
Burst Balloons
Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.
Find the maximum coins you can collect by bursting the balloons wisely.
Note:
You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them. 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
Example:
Input: [3,1,5,8]
Output: 167
Explanation: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
Solution: In this problem, when you burst a ballon, the left and right become adjacent and have effects on the maxCoins in the future. So we need reverse thinking, the coins you get for a balloon does not depend on the balloons already burst. Therefore, instead of divide the problem by the first balloon to burst, we divide the the problem by the last balloon to burst.
For the first we have nums[i-1]nums[i]nums[i+1] for the last we have nums[-1]nums[i]nums[n]. We can see that the balloons is again separated into 2 sections. But this time since the balloon i is the last balloon of all to burst, the left and right section now has well defined boundary and do not affect each other! Therefore we can do either recursive method with memoization or dp.
// Divide and conquer with memorization
public int maxCoins(int[] iNums) {
int[] nums = new int[iNums.length + 2];
int n = 1;
for (int x : iNums) {
if (x > 0) // remove zero balloons
nums[n++] = x;
}
// add 2 imaged balloons!
nums[0] = nums[n++] = 1;
int[][] memo = new int[n][n];
return burstBalloons(memo, nums, 0, n - 1);
}
public int burstBalloons(int[][] memo, int[] nums, int left, int right) {
if (memo[left][right] > 0)
return memo[left][right];
int max = 0;
for (int i = left + 1; i < right; i++) {
// treat i as the last balloon
int coins = nums[left] * nums[i] * nums[right];
max = Math.max(max, burstBalloons(memo, nums, left, i) + coins + burstBalloons(memo, nums, i, right));
}
return memo[left][right] = max;
}
// DP
public int maxCoins2(int[] iNums) {
int[] nums = new int[iNums.length + 2];
int n = 1;
for (int x : iNums) {
if (x > 0)
nums[n++] = x;
}
nums[0] = nums[n++] = 1;
int[][] dp = new int[n][n];
for (int k = 2; k < n; k++)
for (int left = 0; left < n - k; left++) {
int right = left + k;
for (int i = left + 1; i < right; ++i) {
int coins = nums[left] * nums[i] * nums[right];
dp[left][right] = Math.max(dp[left][right], dp[left][i] + coins + dp[i][right]);
}
}
return dp[0][n - 1];
}
Minimum Cost to Merge Stones
/**
* There are n piles of stones arranged in a row. The ith pile has stones[i] stones.
*
* A move consists of merging exactly k consecutive piles into one pile, and the cost of this move
* is equal to the total number of stones in these k piles.
*
* Return the minimum cost to merge all piles of stones into one pile. If it is impossible, return
* -1.
*
* <pre>
* Example 1:
*
* Input: stones = [3,2,4,1], k = 2
* Output: 20
* Explanation: We start with [3, 2, 4, 1].
* We merge [3, 2] for a cost of 5, and we are left with [5, 4, 1].
* We merge [4, 1] for a cost of 5, and we are left with [5, 5].
* We merge [5, 5] for a cost of 10, and we are left with [10].
* The total cost was 20, and this is the minimum possible
* </pre>
*
* https://leetcode.com/problems/minimum-cost-to-merge-stones/
*/
public class MinCostToMergeStones {
public int mergeStones(int[] stones, int k) {
int len = stones.length;
// Check if the input can be merged
// k - 1 as it's to merge k piles into 1 pile
// len - 1 as the very last time is to merge k piles
if ((len - 1) % (k - 1) > 0) {
return -1;
}
// Calculate prefix sum
int[] preSum = new int[len + 1];
for (int i = 0; i < len; i++) {
preSum[i + 1] = preSum[i] + stones[i];
}
// Bottom up DP approach where each entry represents the min cost for current sub array
int[][] dp = new int[len][len];
// span is the length of current sub array
for (int span = k; span <= len; span++) {
for (int left = 0; left + span <= len; left++) {
int right = left + span - 1; // span/k is 1 based
// Initialize as max value
dp[left][right] = Integer.MAX_VALUE;
// Since k is 1 based and we can merge only k piles.
for (int split = left; split < right; split += (k - 1)) {
// Left side to be merged into 1 pile for sure, but right side to 1 + k - 2 piles
dp[left][right] = Math.min(dp[left][right], dp[left][split] + dp[split + 1][right]);
}
// The very last time to merge rest k piles if applicable
if ((left - right) % (k - 1) == 0) {
dp[left][right] += (preSum[right + 1] - preSum[left]);
}
}
}
return dp[0][len - 1];
}
}
Predict the Winner
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
Example 2:
Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
Solution 1: Use Recursion to keep tracking current larger effective score. O(n^2), O(n^2).
public boolean predictTheWinner(int[] nums) {
Integer[][] memo = new Integer[nums.length][nums.length];
return predictWinner(nums, 0, nums.length - 1, memo) >= 0;
}
public int predictWinner(int[] nums, int s, int e, Integer[][] memo) {
if (s == e)
return nums[s];
// remove duplicate calls
if (memo[s][e] != null)
return memo[s][e];
// pick from left, and minus player 2's max
int a = nums[s] - predictWinner(nums, s + 1, e, memo);
// pick from right, and minus player 2's max
int b = nums[e] - predictWinner(nums, s, e - 1, memo);
// pick the bigger effective score
return memo[s][e] = Math.max(a, b);
}
Solution 2: 1-D Dynamic Programming. O(n^2), O(n)
The current effective score isn’t dependent on the elements outside the range [x, y]. We can say that if know the maximum effective score possible for the subarray nums[x+1,y] and nums[x,y−1], we can easily determine the maximum effective score possible for the subarray nums[x,y].
// dp[i,j] = max(nums[i] − dp[i + 1][j], nums[j] − dp[i][j−1])
public boolean predictTheWinner2(int[] nums) {
int[] dp = new int[nums.length];
// starts from the right side
for (int s = nums.length; s >= 0; s--) {
for (int e = s + 1; e < nums.length; e++) {
int a = nums[s] - dp[e];
int b = nums[e] - dp[e - 1];
dp[e] = Math.max(a, b);
}
}
return dp[nums.length - 1] >= 0;
}
Paint House
There are a row of n houses, each house can be painted with one of the three colors: red, blue or green. The cost of painting each house with a certain color is different. You have to paint all the houses such that no two adjacent houses have the same color.
The cost of painting each house with a certain color is represented by a n x 3 cost matrix. For example, costs[0][0] is the cost of painting house 0 with color red; costs[1][2] is the cost of painting house 1 with color green, and so on… Find the minimum cost to paint all houses.
Input: [[17,2,17],[16,16,5],[14,3,19]]
Output: 10
Explanation: Paint house 0 into blue, paint house 1 into green, paint house 2 into blue.
Minimum cost: 2 + 5 + 3 = 10.
public int minCost(int[][] costs) {
if (costs == null || costs.length == 0 || costs[0].length == 0)
return 0;
int n = costs.length, k = costs[0].length;
int[][] dp = new int[n][k];
for (int i = 0; i < n; i++)
Arrays.fill(dp[i], Integer.MAX_VALUE);
for (int i = 0; i < n; i++) {
for (int j = 0; j < k; j++) {
if (i == 0) {
dp[i][j] = costs[i][j];
} else {
// try other different colors
for (int l = 0; l < k; l++) {
if (l == j)
continue;
dp[i][j] = Math.min(dp[i][j], dp[i - 1][l] + costs[i][j]);
}
}
}
}
return Arrays.stream(dp[n - 1]).min().getAsInt();
}
// When only 3 colors!
public int minCost2(int[][] costs) {
if (costs == null || costs.length == 0)
return 0;
for (int i = 1; i < costs.length; i++) {
costs[i][0] += Math.min(costs[i - 1][1], costs[i - 1][2]);
costs[i][1] += Math.min(costs[i - 1][0], costs[i - 1][2]);
costs[i][2] += Math.min(costs[i - 1][1], costs[i - 1][0]);
}
int n = costs.length - 1;
return Math.min(Math.min(costs[n][0], costs[n][1]), costs[n][2]);
}
Paint House III
/**
*
* There is a row of m houses in a small city, each house must be painted with one of the n colors
* (labeled from 1 to n), some houses that have been painted last summer should not be painted
* again.
*
* A neighborhood is a maximal group of continuous houses that are painted with the same color.
*
* For example: houses = [1,2,2,3,3,2,1,1] contains 5 neighborhoods [{1}, {2,2}, {3,3}, {2}, {1,1}].
*
* Given an array houses, an m x n matrix cost and an integer target where:
*
* houses[i]: is the color of the house i, and 0 if the house is not painted yet. <br>
* cost[i][j]: is the cost of paint the house i with the color j + 1. <br>
* Return the minimum cost of painting all the remaining houses in such a way that there are exactly
* target neighborhoods. If it is not possible, return -1. <br>
*
* <pre>
* Example 1:
*
* Input: houses = [0,0,0,0,0], cost = [[1,10],[10,1],[10,1],[1,10],[5,1]], m = 5, n = 2, target = 3
* Output: 9
* Explanation: Paint houses of this way [1,2,2,1,1]
* This array contains target = 3 neighborhoods, [{1}, {2,2}, {1,1}].
* Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
* </pre>
*
* https://leetcode.com/problems/paint-house-iii/
*/
public class PaintHouseIII {
public int minCost(int[] houses, int[][] costs, int target) {
int[][][] memo = new int[costs.length][target + 1][costs[0].length + 1];
return minCost(houses, costs, 0, -1, target, memo);
}
public int minCost(int[] houses, int[][] costs, int currentHouse, int prevColor, int target, int[][][] memo) {
if (currentHouse >= houses.length)
return target == 0 ? 0 : -1;
if (target < 0)
return -1;
if (prevColor != -1 && memo[currentHouse][target][prevColor] != 0) {
return memo[currentHouse][target][prevColor];
}
int minCost = -1;
int currentColor = houses[currentHouse];
if (currentColor == 0) {
// Try out all different colors
for (int chosenColor = 1; chosenColor <= costs[currentHouse].length; chosenColor++) {
int nextCost = minCost(houses, costs, currentHouse + 1, chosenColor, target - (chosenColor == prevColor ? 0 : 1), memo);
// If chosenColor can reach target eventually
if (nextCost != -1) {
nextCost = (currentColor != 0 ? 0 : costs[currentHouse][chosenColor - 1]) + nextCost;
minCost = minCost == -1 ? nextCost : Math.min(minCost, nextCost);
}
}
} else {
int nextCost = minCost(houses, costs, currentHouse + 1, currentColor, target - (currentColor == prevColor ? 0 : 1), memo);
minCost = minCost == -1 ? nextCost : Math.min(minCost, nextCost);
}
if (prevColor != -1) {
memo[currentHouse][target][prevColor] = minCost;
}
return minCost;
}
}