In an interview, when someone asks a system design question. You should have a conversation in which you demonstrate an ability to think creatively, understand design trade-offs, and attack unfamiliar problems. You should sketch key data structures and algorithms, as well as the technology stack (programming language, libraries, OS, hardware, and services) that you would use to solve the problem.
System Design Patterns
| Design Principle | Key Points |
|---|---|
| Algorithms and Data Structures | Identify the basic algorithms and data structures |
| Decomposition and Design Patterns | Split the architecture, functionality and code into manageable, reusable components. The subject of design patterns is concerned with finding good ways to achieve code-reuse. Broadly speaking, design patterns are grouped into creational, structural, and behavioral patterns. |
| Scalability and Parallelism | Break the problem into subproblems that can be solved relatively independently on different machines. Shard data across machines to make it fit. Decouple the servers that handle writes from those that handle reads. Use replication across the read servers to gain more performance. Consider caching computation and later look it up to save work. |
Design a Spell Checker
Design a good spelling correction system can be challenging.
Solution: The basic idea behind most spelling correction system is that the misspelled word’s Levenshtein (edit) distance from the intended word tends to be very small (one or two edits). Hence, if we keep a hash table for all the words in the dictionary and look for all the words that have a Levenshtein distance of 2 from the text, it is likely that the intended word will be found in this set.
The total number of ways of selecting any two characters is n(n-1)/2, and each character can be changed to one of (m-1) other chars. Therefore, the number of lookups is n(n-1)(m-1)^2/2.
It is important to provide a ranked list of suggestions to the users, with the most likely candidates are at the beginning of the list.
- Context based: track what words used in the text. (Viterbi Algorithm)
- Language words differences, or culture differences.
- Typing errors model: can be modeled based on keyboard layouts.
- Phonetic modeling: when knows how the words sounds but does not know the exact spelling.
- History of refinements: by first entering a misspelled word and then correcting it.
- Stemming: by keeping only the stemmed version of each word.
Design Gmail System
Based on Reactive Design Pattern (Responsive, Resilient, Elastic, Message-Driven).
-
Coping with load by splitting a system into distribution parts. Sharding datasets or computational resources solves the problem of providing sufficient resources for the nominal case. (Sharding Pattern): Combine Multiple IDs
-
Coping with failure by using active-passive replication. Replicas agree on which one of them can accept updates. Fail-over to a different replica requires consensus among the remaining ones when the active replica no longer responds. Especially Gmail services should provide consistency to the user.
-
Making the system responsive by employing circuit breakers and flow control between front end and web servers, also between web servers and back-end services. We can even switch the entire application to offline mode when only a small part of the back-end are unavailable.
-
Avoiding the ball of mud by decomposing the multitude of services. Such as the principle of message-flow design would be that the service that handles email composition probably should not talk directly to the contact pop-up service. Also consider Micro services pattern.
-
Integrating nonreactive components by measuring the latency of external API. Dedicate a process/thread to this encapsulated form of external API call. If latency exceeds the acceptable threshold, will either response to requests with a rejection or a temporary failure code.
Reacting to users and failures, losing strong consistency
Systems with an inherently distributed design are built on a set of principles called BASE: Basically available; Soft state (state needs to be actively maintained instead of persisting by default); Eventually consistent.
The last point means that modifications to the data need time to travel between distributed replicas, and during this time it is possible for external observers to see data that are inconsistent. The qualification “eventually” means the time window during which inconsistency can be observed after a change is bounded; when the system does not receive modifications any longer and enters a quiescent state, it will eventually become fully consistent again.
In the example of editing a shared document, this means although you see your own changes immediately, you might see the other’s changes with some delay; and if conflicting changes are made, then the intermediate states seen by both users may be different. But once the incoming streams of changes end, both views will eventually settle into the same state for both users.
The inconsistency observed in eventually consistent systems is also short-lived; the delay between changes being made by one user and being visible to others is on the order of tens or maybe hundreds of milliseconds, which is good enough for collaborative document editing.
Apply the Actor Model
The Actor model is a model of concurrent computation in which all communication occurs between entities called Actors, via message passing on the sending side and mailbox queues on the receiving side. The Erlang programming language, one of the earliest to support Reactive application development, uses Actors as its primary architectural construct. With the success of the Akka toolkit on the JVM, Actors have had a surge in popularity of late.
Handle the Stemming Problem
Stemming is the process of reducing all variants of a given word to one common root, like {computers, computer, compute, computation} to compute. How to design a stemming algorithm that is fast and effective.
Solution: Most stemming systems are based on simple rewrite rules, e.g., remove suffixes of the form “es”, “s”, and “ation”. sometimes need to replaces suffix. Other approaches include the use of stochastic methods to learn rewrite rules and n-gram based approaches where we look at the surrounding words.
One way of efficiently performing the transformation rules is to build a finite state machine based on all the rules.
Design a Scalable Priority System
Design a system for maintaining a set of prioritized jobs that implements Insert, Delete and Fetch the highest priority job. Assume the set cannot fit into a single machine’s memory.
Solution: If we have enough RAM on a single machine, the most simple solution would be to maintain a min-heap where entries are ordered by their priority. An additional hash table can be used to map jobs to their corresponding entry in the min-heap to make deletions fast.
A more scalable solution entails partitioning the problem across multiple machines. One approach is to apply a hash function to the job ids and partition the resulting hash codes into ranges, one per machine. Insert as well as delete require communication with just one server. To do extract-min, we send a lookup minimum message to all the machines, infer the min from their responses, and the delete it.
If many clients are trying to do this operation at the same time, we may run into a situation where most clients will find that the min event they are trying to extract has already been deleted. If the throughput of this service can be handled by a single machine, we can make one server solely responsible for responding to all the requests. This server can prefetch the top hundred or so events from each of the machines and keep them in a heap.
In many applications, we do not need strong consistency guarantees. A client could pick one of the machines at random (or round-robin), and request the highest priority jobs. This would work well for the distributed crawler application, but not suited to event-driven simulation because of dependencies.
Consider resilience: if a node fails, all list of work on that node fails as well. It is better to have nodes to contain overlapped lists (replicate a copy to it’s predecessor) and the dispatching node in this case will handle duplicates. The lost of a node shouldn’t result in full re-hashing – the replacement node should handle only new jobs. Consistent hashing can be used to achieve this.
A front-end caching server can become a bottleneck. This can be avoided by using replication, i.e, multiple servers which duplicate each other. There could be possible several ways to coordinate them: use non-overlapping lists, keep a blocked job list, return a random job from the jobs with highest priority.
Design a Recommendation System
Design a system that automatically generates a sidebar of related articles.
Solution:
-
Some simple solutions: Add articles that have proved to be popular recently; Link to recent news articles; Tag articles with related keywords (i.e., finance, sports, and politics); These tags could also come from the HTML meta-tags or page titles.
-
We could also provide randomly selected articles to a random subset of readers and see how popular these articles proved to be. The popular articles could then be shown more frequently. (Leads to No.3)
-
Build a scoring mechanism that takes various features as signals and computes a final score for each article (link/like/comment numbers).
-
A more sophisticated level, use automatic textual analysis, where a similarity is defined between pairs of articles: This similarity is a real number and measures how many words are common to the two. Several issues come up, such as the fact that frequently occurring words such as “for” and “the” should be ignored and that having rare words such as “arbitrage” and “diesel” in common is more significant that having say, “sale” and “international”.
-
Textual analysis has problems, such as the fact that two words may have the same spelling but completely different meanings (anti-virus means different things in the context of articles on medical and computer). One way to augment textual analysis is to use collaborative filtering–using information gleaned from many users. For example, by examining cookies and timestamps in the web server’s log files, we can tell what articles individual users have read. If we see many users have read both A and B in a single session, we might want to recommend B to anyone reading A.
Design an Online Advertising System
Solution: (skipped some other details)
-
Consider the stakeholders separately (Users, Advertisers, Search Engine Companies).
-
The ad-serving system would build a specialized data structure, such as a decision tree from the ads database. It chooses ads from the database of ads based on their “relevance” to the search. In addition to keywords, the ad-serving systems can use knowledge of the user’s search history, bidding amount, the time scheduler, user location, device type, gender, etc. Many strategies can be envisioned here for estimating relevance.
-
The ads could be added to the search results by embedding JavaScript in the results page. Which pulls in the ads from the ad-serving system directly. This helps isolate the latency of serving search results from the latency of serving ad results.
Optimize Large Files Distribution
Design an efficient way of copying one thousand files each 100 kilobytes in size from a single lab server to each of 1000 servers in a distant data center.
Solution:
-
Assume that the bandwidth from the lab machine is a limiting factor. We can do some trivial optimizations, such as combining the articles into a single file and compressing this file.
-
We can copy the file from the lab machine to a single machine in the data center first. And have each machine that has received the file initiate copies to the machines that have not yet received the file. (In theory, this leads to an exponential reduction.)
-
How should the knowledge of machines which do not yet have copies of the file be shared? There can be a central repository or servers can simply check others by random selection.
-
If the bandwidth between machines in a data center is not a constant, Servers close to each other, e.g. in the same rack, should prefer communicating with each other.)
-
Finally, please note there are open source solutions to this problem, such as Unison and BitTorrent.
Encode and Decode TinyURL
TinyURL is a URL shortening service where you enter a URL such as https://leetcode.com/problems/design-tinyurl and it returns a short URL such as http://tinyurl.com/4e9iAk.
Solution:
-
Random fixed-length encoding, can be encoded up to 62^6! And also can increase the number of encodings possible as well by increasing the length. It’s hard to predict since the random numbers are used.
-
To build the index, instead of using Map, we could build index with a 64-way B-tree or Trie-tree, and each leave has the address pointer which points to the long url in disk. So we can handle large volume of long urls and distribute to different partitions or nodes.
-
We can even build a LFU (Least Frequently Used Cache) to cache with popular urls and also periodically clean up the legacy URLs.
public class TinyUrl { String alphabet = “0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ”; Map<String, String> map = new HashMap<>(); Random rand = new SecureRandom(); String key = getRand();
public String getRand() {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 6; i++) {
sb.append(alphabet.charAt(rand.nextInt(62)));
}
return sb.toString();
}
public String encode(String longUrl) {
while (map.containsKey(key)) {
key = getRand();
}
map.put(key, longUrl);
return "http://tinyurl.com/" + key;
}
public String decode(String shortUrl) {
return map.get(shortUrl.replace("http://tinyurl.com/", ""));
} }
MapReduce Design Pattern
MapReduce is a computing paradigm for processing data that resides on hundreds of computers, which has been popularized recently by Google, Hadoop, and many others. MapReduce is more of a framework than a tool. You have to design and fit your solution into the framework of map and reduce. Several other open source projects have been built with Hadoop at their core, like Pig, Hive, HBase, Mahout, and ZooKeeper.
Hadoop MapReduce jobs are divided into a set of map tasks and reduce tasks that run in a distributed fashion on a cluster of computers. Each task works on the small subset of the data it has been assigned so that the load is spread across the cluster. The map tasks generally load, parse, transform, and filter data. Each reduce task is responsible for handling a subset of the map task output. Intermediate data is then copied from mapper tasks by the reducer tasks in order to group and aggregate the data.
The input to a MapReduce job is a set of files in the data store that are spread out over the Hadoop Distributed File System (HDFS). In Hadoop, these files are split with an input format, which defines how to separate a file into input splits. An input split is a byte-oriented view of a chunk of the file to be loaded by a map task.
Each map task in Hadoop is broken into the following phases: record reader, mapper, combiner, and partitioner. The output of the map tasks, called the intermediate keys and values, are sent to the reducers. The reduce tasks are broken into the following phases: shuffle, sort, reducer, and output format. The nodes in which the map tasks run are optimally on the nodes in which the data rests. This way, the data typically does not have to move over the network and can be computed on the local machine.
Pig and Hive are higher-level abstractions of MapReduce. They provide an interface that has nothing to do with “map” or “reduce,” but the systems interpret the higher-level language into a series of MapReduce jobs. Much like how a query planner in an RDBMS translates SQL into actual operations on data, Hive and Pig translate their respective languages into MapReduce operations.
public class CommentWordCount {
public static class WordCountMapper extends Mapper<Object, Text, Text, IntWritable> {
private final static IntWritable one = new IntWritable(1);
private Text word = new Text();
public void map(Object key, Text value, Context context) throws IOException, InterruptedException {
// Parse the input string into a nice map
Map<String, String> parsed = MRDPUtils.transformXmlToMap(value.toString());
// Grab the "Text" field, since that is what we are counting over
String txt = parsed.get("Text");
// .get will return null if the key is not there
if (txt == null) {
// skip this record
return;
}
// Unescape the HTML because the data is escaped.
txt = StringEscapeUtils.unescapeHtml(txt.toLowerCase());
// Remove some annoying punctuation
txt = txt.replaceAll("'", ""); // remove single quotes (e.g., can't)
txt = txt.replaceAll("[^a-zA-Z]", " "); // replace the rest with a space
// Tokenize the string by splitting it up on whitespace into
// something we can iterate over,
// then send the tokens away
StringTokenizer itr = new StringTokenizer(txt);
while (itr.hasMoreTokens()) {
word.set(itr.nextToken());
context.write(word, one);
}
}
}
public static class IntSumReducer extends Reducer<Text, IntWritable, Text, IntWritable> {
private IntWritable result = new IntWritable();
public void reduce(Text key, Iterable<IntWritable> values, Context context) throws IOException, InterruptedException {
int sum = 0;
for (IntWritable val : values) {
sum += val.get();
}
result.set(sum);
context.write(key, result);
}
}
public static void main(String[] args) throws Exception {
Configuration conf = new Configuration();
String[] otherArgs = new GenericOptionsParser(conf, args).getRemainingArgs();
if (otherArgs.length != 2) {
System.err.println("Usage: CommentWordCount <in> <out>");
System.exit(2);
}
Job job = new Job(conf, "StackOverflow Comment Word Count");
job.setJarByClass(CommentWordCount.class);
job.setMapperClass(WordCountMapper.class);
job.setCombinerClass(IntSumReducer.class); // use combiner to reduce in local first!
job.setReducerClass(IntSumReducer.class);
job.setOutputKeyClass(Text.class);
job.setOutputValueClass(IntWritable.class);
FileInputFormat.addInputPath(job, new Path(otherArgs[0]));
FileOutputFormat.setOutputPath(job, new Path(otherArgs[1]));
System.exit(job.waitForCompletion(true) ? 0 : 1);
}
}
Bloom Filter Pattern
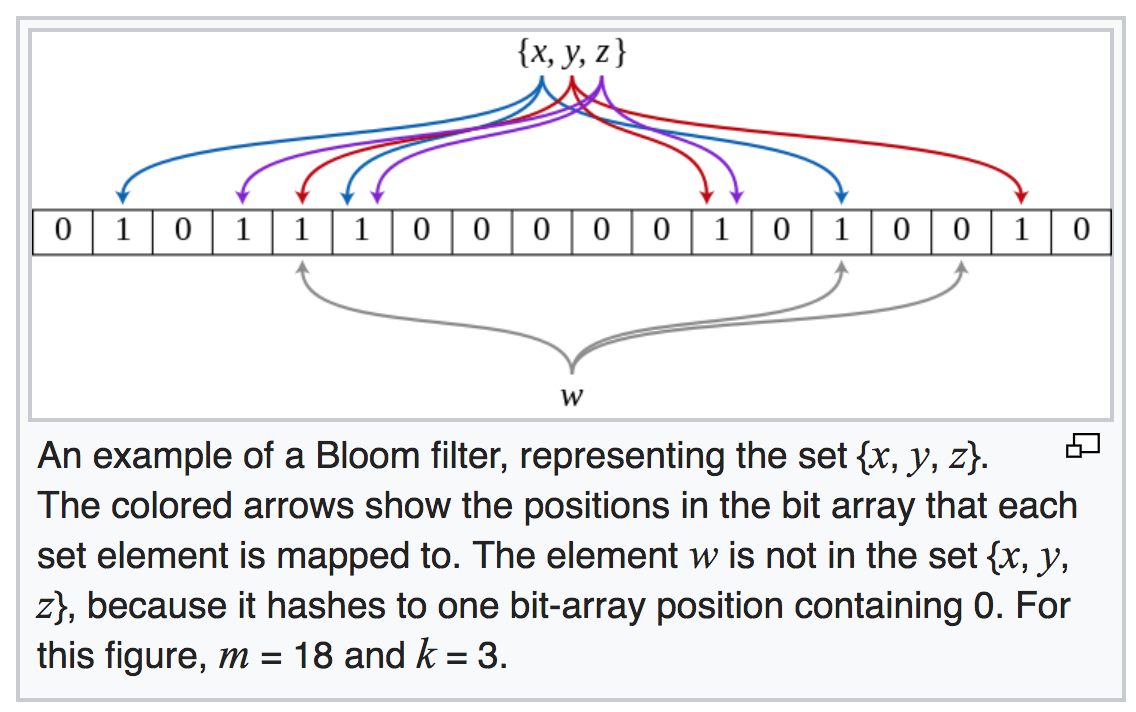
An empty Bloom filter is a bit array of m bits, all set to 0. There must also be k different hash functions defined, each of which maps or hashes some set element to one of the m array positions, generating a uniform random distribution.
To add an element, feed it to each of the k hash functions to get k array positions. Set the bits at all these positions to 1.
To query for an element (test whether it is in the set), feed it to each of the k hash functions to get k array positions. If any of the bits at these positions is 0, the element is definitely not in the set – if it were, then all the bits would have been set to 1 when it was inserted. If all are 1, then either the element is in the set, or the bits have by chance been set to 1 during the insertion of other elements, resulting in a false positive. In a simple Bloom filter, there is no way to distinguish between the two cases, but more advanced techniques can address this problem.
This classic example is using bloom filters to reduce expensive disks (or network) lookups for non-existent keys.
If the element is not in the bloom filter, then we know for sure we don’t need to perform the expensive lookup. On the other hand, if it is in the bloom filter, we perform the lookup, and we can expect it to fail some proportion of the time (the false positive rate).
The false positive rate is a function of the bloom filter’s size and the number and independence of the hash functions used. As more elements are added to the set, the probability of false positives increases.
Problem: Given a list of user’s comments, filter out a majority of the comments that do not contain a particular keyword. We can train a bloom filter with a hot list of keywords.
https://www.jasondavies.com/bloomfilter/ https://en.wikipedia.org/wiki/Bloom_filter
Top Ten Pattern
Problem: Given a list of user information, output the information of the top ten users based on reputation.
The top ten pattern utilizes both the mapper and the reducer. The mappers will find their local top K, then all of the individual top K sets will compete for the final top K in the reducer. Since the number of records coming out of the mappers is at most K and K is relatively small, we’ll only need one reducer.
Microservices Design
Microservices is a form of service-oriented architecture style wherein applications are built as a collection of different smaller services rather than one whole app. These independent applications can run and scale on their own and may be created using different coding and languages.
Advantages of microservice architecture: Focus on a specific requirement; developed by a small team with productivity; Loosely coupled, can be developed, deployed and scaled on their own; Easy to integrate with 3rd parties.
The popular microservice framework:
-
Spring Boot. Which has all the infrastructures that you applications need: Framework, Cloud, Data, Batch, Security, Social, Mobile, and REST Docs.
-
Play Framework: Play Framework gives you an easier way to build, create and deploy Web applications using Scala and Java. Play Framework is ideal for RESTful application that requires you to handle remote calls in parallel. It is also very modular and supports async. Play Framework also has one of the biggest communities out of all microservices frameworks.
-
Swagger. Helps you in documenting API as well as gives you a development portal, which allows users to test your APIs.
Game Design Questions
Zobrist Hashing for Chess
Design a hash function for chess game states. Your function should take a state and the hash code for that state, and a move, and efficiently compute the hash code for the updated state.
Solution:
The state of a game of chess is determined by what piece is present on each square, each square may be empty, or have one of six classes of pieces; each piece may be black or white. Thus log(1+6x2) = 4 bits suffice per square, which means a total of 64 x 4 = 256 bits can represent the state of the chess board. But this way uses more store space and can not be efficiently computed based on incremental changes to the board.
A straightforward hash function is to treat the board as a sequence of 64 base 13 digits. There is one digit per square, with the squares numbered from 0 to 63. Each digit encodes the state of a square: blank, white pawn, white rook,…,white king, blank pawn,…,blank king. We use the hash function as \(\sum_{i=0}^{63}c_ip^i\), where \(c_i\) is the digit in location i, and p is a prime number.
Note that this hash function has some ability to be updated incrementally. If, for example, a black knight taken by a white bishop the new hash code can be computed by subtracting the terms corresponding to the initial location of the knight and bishop, and adding a term for a blank at the initial location of the bishop and a term for the bishop at the knight’s original position.
Now let’s describe the Zobrist Hashing function which is much faster to update. The main purpose of Zobrist hash codes in chess programming is to get an almost unique index number for any chess position/state (chess fingerprint), with a very important requirement that two similar positions generate entirely different indices. These index numbers are used for xor-operation to allow a fast incremental update of the hash key during moves.
At program initialization, we generate an array of random numbers:
- One number for each piece at each square.
- One number to indicate the side to move is black.
- Four numbers to indicate the castling rights.
- Eight numbers to indicate the file of a valid En passant square, if any.
This leaves us with an array with 781 (12 * 64 + 1 + 4 + 8) random numbers. Since pawns don’t happen on first and eighth rank, 12 * 64 should be fine. Usually 64bit are used as a standard size in modern chess programs.
To get a Zobrish hash code of the starting position, we can do the xor-operation for all pieces:
[Hash for White Rook on a1] xor [White Knight on b1] xor [White Bishop on c1] xor ... ( all pieces )
... xor [White castling short] xor [White castling long] xor ... ( all castling rights )
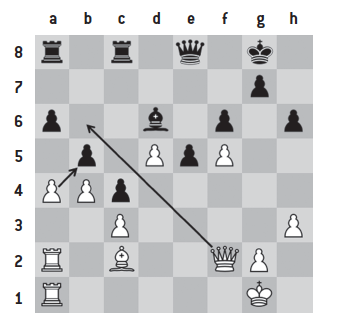
E.g., for a White Knight that jumps from b1 to c3 capturing a Black Bishop, these operations are performed:
[Original Hash of position] xor
[Hash for White Knight on b1] (removing the knight from b1) xor
[Hash for Black Bishop on c3] (removing the captured bishop from c3) xor
[Hash for White Knight on c3] (placing the knight on the new square) xor
[Hash for Black to move] (change sides)
An important issue is the question of what size the hash keys should have. Smaller hash keys are faster and more space efficient, while larger ones reduce the risk of a hash collision. The chance of collisions approaches certainty at around the square root of the number of possible keys. With a 64 bit hash, you can expect a collision after about 2^32 or 4 billion positions.
Zobrist Hashing Implementation
// A program to illustrate Zobrist Hashing Algorithm
#include <bits/stdc++.h>
using namespace std;
unsigned long long int ZobristTable[8][8][12];
// Generates a Randome number from 0 to 2^64-1
unsigned long long int randomInt()
{
uniform_int_distribution<unsigned long long int>
dist(0, UINT64_MAX);
return dist(mt);
}
// This function associates each piece with
// a number
int indexOf(char piece)
{
if (piece=='P')
return 0;
if (piece=='N')
return 1;
if (piece=='B')
return 2;
if (piece=='R')
return 3;
if (piece=='Q')
return 4;
if (piece=='K')
return 5;
if (piece=='p')
return 6;
if (piece=='n')
return 7;
if (piece=='b')
return 8;
if (piece=='r')
return 9;
if (piece=='q')
return 10;
if (piece=='k')
return 11;
else
return -1;
}
// Initializes the table
void initTable()
{
for (int i = 0; i<8; i++)
for (int j = 0; j<8; j++)
for (int k = 0; k<12; k++)
ZobristTable[i][j][k] = randomInt();
}
// Computes the hash value of a given board
unsigned long long int computeHash(char board[8][9])
{
unsigned long long int h = 0;
for (int i = 0; i<8; i++)
{
for (int j = 0; j<8; j++)
{
if (board[i][j]!='-')
{
int piece = indexOf(board[i][j]);
h ^= ZobristTable[i][j][piece];
}
}
}
return h;
}
// Main Function
int main()
{
// Uppercase letters are white pieces
// Lowercase letters are black pieces
char board[8][8] =
{
"---K----",
"-R----Q-",
"--------",
"-P----p-",
"-----p--",
"--------",
"p---b--q",
"----n--k"
};
initTable();
unsigned long long int hashValue = computeHash(board);
printf("The hash value is : %llu\n", hashValue);
//Move the white king to the left
char piece = board[0][3];
board[0][3] = '-';
hashValue ^= ZobristTable[0][3][indexOf(piece)];
board[0][2] = piece;
hashValue ^= ZobristTable[0][2][indexOf(piece)];
printf("The new hash vlaue is : %llu\n", hashValue);
// Undo the white king move
piece = board[0][2];
board[0][2] = '-';
hashValue ^= ZobristTable[0][2][indexOf(piece)];
board[0][3] = piece;
hashValue ^= ZobristTable[0][3][indexOf(piece)];
printf("The old hash vlaue is : %llu\n", hashValue);
return 0;
}
Output
The hash value is : 14226429382419125366
The new hash vlaue is : 15124945578233295113
The old hash vlaue is : 14226429382419125366
Design the Chess Game
Basic Object Design
- Game:
- Contains the Board and 2 Players
- Commands List (for history tracking)
- isOver(), isStaleMate(), isCheckMate()
- Board (No Singleton):
- Hold spots with 8*8
- Initialize the piece when game start
- Move Piece
- Remove Piece
- Replace Piece
- Can move to location(int startX, int startY, int endX, int endY).
- Spot:
- Hold Pieces
- Piece (Abstract):
- Hold the color to represent the affiliation.
- Extended by concreted classes with 8 Pawns, 2 Rooks, 2 Bishops, 2 Knights, 1 Queen, 1 King.
- Concreted classes define the detail step approach.
- Defined move rules: isValidMove(), checkPromote()
- Player (Abstract):
- Has a list of piece reference it owns.
- Concreted classes for Human and Computer players
- isChecked()
- Command
- Piece
- Destination x, y
- Game Engine
- Transposition Table
- Zobrist Hashing
- Minimax Evaluation
- Game Tree
Web Version: Consider Session (Authentication), Ajax, WebSocket, or Comet (Streaming or Long Polling), Controller (RESTful API), Scalability, Data Model. Design Pattern: MVC, Observer, Listener, Singleton.
Make a Move
What a full “move” entails in chess:
- Player chooses piece to move.
- Piece makes legal move according to its own move rules.
- In addition to purely move-based rules, there’s also capture logic, so a bishop cannot move from a1-h8 if there’s a piece sitting on c3.
- If the player was previous under check and the move does not remove the check, it must be undone.
- If the move exposes check, it must be undone / disallowed.
- If player captures a piece, remove the piece (including en passant!)
- If the piece is a pawn reaching the back rank, promote it.
- If the move is a castling, set the new position of the rook accordingly. But a king and rook can only castle if they haven’t moved, so you need to keep track of that. And if the king moves through a check to castle, that’s disallowed, too.
- If the move results in a stalemate or checkmate, the game is over.
And the move method would contain all the code to validate the steps above:
- Check Piece.isValidMove(currentSpot, newSpot); - probably need castling logic here since king moves more than 1 space and rook jumps the king)
- Check Player.isChecked() (which is just sugar for Player.Pieces[“King”].CanBeCaptured() - more fun logic here!)
- Check if newSpot contains a piece and if so, newSpot.Piece.Remove();
- Build some logic to call Piece.checkEnPassant() (Piece is pawn, first move, 2 steps, past an enemy pawn who moved into capturing position on previous move - have fun with that!)
- Piece.checkPromote() (Piece is pawn, move ends on opposing player’s back rank)
- Check if Game.isOver(), which checks Game.isStaleMate() and Game.isCheckMate().
Transposition Table
The chess game will often have to consider the same position several times. So most chess engines implement a Transposition Table that stores previously searched positions and evaluations.
The transposition table should store 15%-20% positions/entries ahead of time (NO NEED ALL), and it has to be efficient because we will be storing and searching more useless entries.
To calculate the unique identify for the game state. We can use Zobrist Hashing as described above.
Transposition Table Contents:
- Hash: This is a Zobrist Hash representing the chess position (game state)
- Depth: The depth remaining in the alpha beta search. So depth 5 would mean the score is recorded for a 5 ply search. This can also be referred to as the Depth of the Search Tree.
- Score: The evaluation score for the position.
- Ancient: Boolean flag, if false the node will not be replaced with a newer entry.
- Node Type: There are 3 node types, Exact, Alpha and Beta. Exact means this is an exact score for the tree. An Alpha Node Type means the value of the node was at most equal to Score. The Beta Node Type means the value is at least equal to score.
Minimax Evaluation
Implement a function that calculates the value of the board depending on the placement of pieces on the board. This function is often known as Evaluation Function. We can use Minimax Algorithm.
A Minimax algorithm is a recursive algorithm for choosing the next move in an n-player game, usually a two-player game. A value is associated with each position or state of the game. This value is computed by means of a position evaluation function and it indicates how good it would be for a player to reach that position. The player then makes the move that maximizes the minimum value of the position resulting from the opponent’s possible following moves. If it’s A’s turn to move, A gives a value to each of this legal movies.
The algorithm can be thought of as exploring the nodes of a game tree. The effective branching factor of the tree is the average number of children of each node (i.e., the average number of legal moves in a position). The number of nodes to be explored usually increases exponentially with the number of plies (it is less than exponential if evaluating forced moves or repeated positions). The number of nodes to be explored for the analysis of a game is therefore approximately the branching factor raised to the power of the number of plies. It is therefore impractical to completely analyze games such as chess using the minimax algorithm.
Design Battleship Game
Basic Object Design
- Game:
- Contains Boards (4 Grids) and 2 Players
- loadGame(), startGame(), saveGame(), isGameOver()
- Commands list (for history tracking)
- Use a variable
shiftto count each round and decide whose turn, i.e. shift = 3 -> shift % 2 = 1 -> player 1
- Board/Grid:
- ShipGrid (primary) and ShotGrid
- Hold spots and status int[10][10]
- Set<Coordinate> taken
- placeShip(Ship s)
- placePeg(Peg p)
- setShipHitAt(int x, int y)
- Ship (Abstract):
- numHitPoints, numHitsTaken
- x, y location and Orientation
- Concreted classes: Carrier(5), Battleship(4), Cruiser(3), Submarine(3) and Destroyer(2)
- isHit(), isSunk()
- Peg
- Color (White, Red)
- With x, y location
- Build a picture of the opponent’s fleet
- Player (Abstract):
- setHits(), setMisses(), setShotsFired()
- Concreted classes for Human and Computer players
- The Computer player can be configured to different level
- Game Engine
- Probability Calculator
- Transition Matrix
- Game Tree
Web Based Application
- Design UI with Board/Grid, Buttons
- For every placement, make an Ajax call to update player board object.
- Once user clicks the button, submit the request to Servlet.
- Maintain an available players and occupied players list in an object. (Singleton)
- If the user is first to click the button, generate a key/sessionId and assign it to user, put to the available list.
- When opponent clicks button, check for available user having a key/sessionId. and use the same id to opponent and move both players to occupied list and redirect theme to same url.
- Now every click in the board, send Coordinate to servlet by making an Ajax call, Blacken the Coordinate for both the boards. Also update the turn status based on Ajax response.
- have session timeout set incase one or both users close their browser.
- Design pattern: MVC, Listener, Observer
Probability Calculator
On a 10 x 10 grid, players hide ships of lengths: 5(Carrier), 4(Battleship), 3(Submarine), 3(Cruiser), 2(Destroyer), which results in 17 possible targets out of the total 100 squares.
The first possible strategy is to make shots totally at random. The game will take almost 100 shots to complete as the majority of squares have to be hit in order to ensure that all the ships are sunk. Mathematically, the changes of playing a perfect game will be 17!/(100!/83!).
17!/(100!/83!) = (17x16x15...3x2x1)/(100x99x98...86x85x84)
Initially, shots can be fired at random (Hunt Mode), but once part of a ship has been hit, it’s possible to search up, down, left and right looking for more of the same ship (Target Mode). After a hit, the four surrounding squares are added to a stack of ‘potential’ targets (or less than four if the cell was on an edge/corner or already visited).
Once in Target mode the computer pops off the next potential target off the stack, fires at this location, actions on this (either adding more potential targets to the stack, or popping the next target location off the stack), until either all ships have been sunk or there are no more potential targets in the stack, at which point it returns to Hunt mode and starts firing at random again looking for another ship.
Hunt Mode Algorithm
If it’s early in the game and there are too many configurations to check all of them, shots can be fire at random.
-
Starts with Center: With no information about the board, the algorithm selects one of the center squares because of the edge effect , the middle of the board will score higher than an edge or a corner.
-
Parity: Because the min length of a ship is two units long, no matter how the two unit destroyer is placed on the 1-100 squares, it will cover one odd and one even square. So we can only randomly fire into location with even parity.
Target Mode Algorithm
- Density:
How to calculate the Density score?
We know which ships (and even more importantly what the lengths of the ships) are still active. The algorithm will calculate the most probably location to fire at next based on a superposition of all possible locations the enemy ships could be in.
We start in the top left corner, and try placing a target ship horizontally. If it fits, we increment a value for each cell it lays over as a ‘possible location’. Then we try sliding it over one square and repeating … and so on util we reach the end of the row. Then we move down a line and repeat. Next we repeat the exercise with the ship oriented vertically.
When in hunt mode, there are only three states to worry about: unvisited space, misses and sunk ships. Misses and Sunk ships are treated the same (obstructions that potential ships needed to be placed around). In target mode (where there is at least one hit ship that has not been sunk), the ships can by definition, pass through this location, and so hit squares are treated as unvisited square for deciding if a ship ‘could’ pass through this square, and then a heavy score weighting is granted to possible locations that pass through this hit.
The Linear Theory of A.I.
\(P_{i,\alpha}\) denotes the probability of there being the given ship on the given square. \(i\) ranges from 0 to 99 and \(\alpha\) is one of the ship.
If we had such a matrix, we could figure out the probability of there being at hit on every square by summing over all the ships we have left, i.e.
\[P_i = \sum_{ships left} P_{i,\alpha}\]How do we get \(P_{i,\alpha}\)? We can predict the probability of a particular ship being in a particular square by (1) noting the background probability of that being true, and (2) adding up all of the information I have, weighting it by the appropriate factor. The equation looks as below:
\[P_{i,\alpha} = B_{i,\alpha} + \sum_{j,\beta} W_{i,\alpha,j,\beta}I_{j,\beta}\]\(B_{i,\alpha}\) denotes the background probability of a particular ship being on a particular ship being on a particular spot on the board.
Below battleship board reflects the sum of all the ship background probabilities.
\[B_i = \sum_{all ships} B_{i,\alpha}\]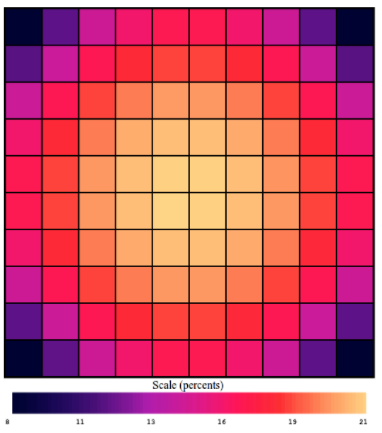
As a game unfolds, we learn a good deal of information about the board, so we need to incorporate this information into our theory of battleship. We call this info matrix \(I_{j,\beta}\).
\(\beta\) marks the kind of information we have about a square: M means a miss, H means a hit, but we don’t know which ship, and CBSDP mark a particular ship hit, which we would know once we sink a ship.
Let’s say, after a few turns, we were told the spot 34 was a hit and also sunk the ship submarine. we would set:
\[I_{34,H} = 1, I_{34,S} = 1, I_{34,M} = I_{34,C} = I_{34,B} = I_{34,D} = I_{34,P} = 0\]Also, we need to take weight into consideration, “the extra probability of there being ship alpha at location i, given the fact that we have the situation beta going on at location j”.
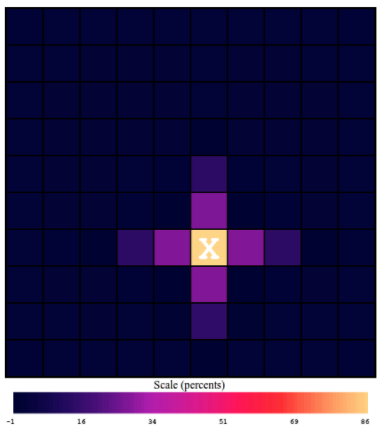
This is a picture of \(W_{i,C,33,M}\), the extra probabilities for each square (i is all of them), of there being a carrier (alpha=C), given that we got a miss (beta=M) on square 33, (j=33).
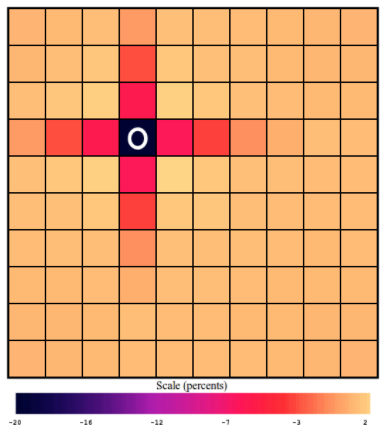
This is a picture of \(W_{i,S,65,H}\), showing the extra probability of there being a submarine (alpha=S), at each square (i is all of them, since its a picture with 100 squares), given that we registered a hit (beta=H) on square 65 (j=65).