Honors Questions
This chapter contains problems that are more difficult to solve. Many of them are commonly asked at interviews, albeit with the expectation that the candidate will not deliver the best solution.
Also categorized with other similar questions to give you an overall ideas around this topic.
Greatest Common Divisor
Design an efficient algorithm for computing the Greatest Common Divisor (GCD) of two nonnegative integers without using multiplication, division or the modulus operators.
Solution:
The straightforward algorithm is based on recursion: if x == y, GCD(x, y) = x; otherwise, if x > y, GCD(x, y) = GCD(x - y, y), or GCD(x, y) == GCD(y, x mod y).
As above algorithm is not allowed, we need to consider bit manipulations with the use cases: both even, both odd; one even and one odd. The time complexity is proportional to the sum of the number of bits in x and y, i.e., O(log(x) + log(y)).
public static long GCD(long x, long y) {
if (x > y) {
return GCD(y, x);
} else if (x == 0 || x == y) { // base case
return y;
} else if ((x & 1) == 0 && (y & 1) == 0) { // x and y are both even
return GCD(x >>> 1, y >>> 1) << 1;
} else if ((x & 1) == 0 && (y & 1) == 1) { // x is even, y is odd
return GCD(x >>> 1, y);
} else if ((x & 1) == 1 && (y & 1) == 0) { // x is odd, y is even
return GCD(x, y >>> 1);
}
return GCD(x, y - x); // x and y are both odd
}
First Missing Positive Entry
Let A be an array of length n. Design an algorithm to find the smallest positive integer which is not present in A. You don’t need to preserve the contents of A. For example, if A = {3, 5, 4, -1, 5, 1, -1}, the smallest positive integer not present in A is 2.
Solution:
We could sort the array A (O(nlog(n))), or store the entries (only positive integers) in A in a hash table (Time(O(n)), Space(O(n)).
Since we don’t need to preserve A, instead of using an external hash table to store the set of positive integers, we can use A itself, if A contains k between 1 and n, we set A[k - 1] to k.
public static int findFirstMissingPositive(List<Integer> A) {
// first pass to save values to proper positions
for (int i = 0; i < A.size(); i++) {
Integer j = A.get(i); // j should be in the index j - 1
while (0 < j && j <= A.size() && !A.get(j - 1).equals(j)) {
Collections.swap(A, i, j - 1);
}
}
// second pass through A to find the missing entry
for (int i = 0; i < A.size(); i++) {
if (A.get(i) != i + 1)
return i + 1;
}
// if not found the entry between 1 and A.size()
return A.size() + 1;
}
Positions Attached By Rooks
Write a program which takes as input a 2D array A of 1s and 0s, where the 0s encode the positions of rooks on an n x m chessboard, and updates the array to contain 0s at all locations which can be attacked by rooks.
Solution:
Make use of the first row and the first column to indicate where there is a rook in this row or column.
public static void positionsAttackedByRooks(int[][] grid) {
int m = grid.length, n = grid[0].length;
boolean hasFirstRowZero = false;
for (int j = 0; j < n; j++) {
if (grid[0][j] == 0) {
hasFirstRowZero = true;
break;
}
}
boolean hasFirstColZero = false;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 0) {
hasFirstColZero = true;
break;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (grid[i][j] == 0) {
grid[i][0] = 0;
grid[0][j] = 0;
}
}
}
for (int i = 1; i < m; i++) {
if (grid[i][0] == 0)
Arrays.fill(grid[i], 0);
}
for (int j = 1; j < n; j++) {
if (grid[0][j] == 0) {
for (int i = 1; i < m; i++) {
grid[i][j] = 0;
}
}
}
if (hasFirstRowZero)
Arrays.fill(grid[0], 0);
if (hasFirstColZero) {
for (int i = 0; i < m; i++) {
grid[i][0] = 0;
}
}
}
Text Justification
Given an array of words and a length L, format the text such that each line has exactly L characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces ‘ ‘ when necessary so that each line has exactly L characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line do not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left justified and no extra space is inserted between words.
For example, words: [“This”, “is”, “an”, “example”, “of”, “text”, “justification.”] L: 16.
Return the formatted lines as:
[
"This is an",
"example of text",
"justification. "
]
Solution:
Solve it on a line-by-line basis, assuming a single blank between pairs of words. Then figure out how to distribute blanks.
public List<String> fullJustify(String[] words, int maxWidth) {
List<String> result = new ArrayList<>();
int start = 0, end = 0;
while (start < words.length) {
int count = words[start].length();
// end is excluded!
end = start + 1;
while (end < words.length) {
// count in the spaces
if (count + 1 + words[end].length() > maxWidth)
break;
count += 1 + words[end].length();
end++;
}
StringBuilder builder = new StringBuilder();
int gaps = end - 1 - start;
// left or middle justified
if (end == words.length || gaps == 0) {
for (int i = start; i < end; i++) {
builder.append(words[i]);
if (i < end - 1)
builder.append(" ");
}
for (int i = builder.length(); i < maxWidth; i++) {
builder.append(" ");
}
} else {
int spaces = (maxWidth - count) / gaps;
int rest = (maxWidth - count) % gaps;
for (int i = start; i < end; i++) {
builder.append(words[i]);
if (i < end - 1) {
builder.append(" ");
for (int j = 0; j < spaces + (i - start < rest ? 1 : 0); j++)
builder.append(" ");
}
}
}
result.add(builder.toString());
start = end;
}
return result;
}
Max Points On a Line
Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.
Solution:
Take each point and calculate the slop to other points, use a hash table to track the counts. The iteration takes O(n^2) time, yielding an overall time bound of O(n^2).
To store the slope key, don’t use the double which has finite precision arithmetic. Instead, let’s use the fraction by calculating their GCD.
public int maxPoints(int[][] points) {
if (points.length <= 2) {
return points.length;
}
int result = 0;
Map<String, Integer> map = new HashMap<>();
for (int i = 0; i < points.length - 1; i++) {
map.clear();
int overlap = 0, max = 0;
for (int j = i + 1; j < points.length; j++) {
int x = points[i][0] - points[j][0];
int y = points[i][1] - points[j][1];
if (x == 0 && y == 0) {
overlap++;
continue;
}
// gcd won't be zero here!
int gcd = getGCD(x, y);
x /= gcd;
y /= gcd;
String slope = x + "," + y;
map.computeIfAbsent(slope, k -> 0);
max = Math.max(max, map.computeIfPresent(slope, (k, v) -> v + 1));
}
// includes itself as well
result = Math.max(result, max + overlap + 1);
}
return result;
}
public int getGCD(int x, int y) {
return (y == 0) ? x : getGCD(y, x % y);
}
Count Inversions
- Global and Local inversions
We have some permutation A of [0, 1, …, N - 1], where N is the length of A.
The number of (global) inversions is the number of i < j with 0 <= i < j < N and A[i] > A[j].
The number of local inversions is the number of i with 0 <= i < N and A[i] > A[i+1].
Return true if and only if the number of global inversions is equal to the number of local inversions.
Example 1:
Input: A = [1,0,2]
Output: true
Explanation: There is 1 global inversion, and 1 local inversion.
Example 2:
Input: A = [1,2,0]
Output: false
Explanation: There are 2 global inversions, and 1 local inversion.
Solution:
Because the count of local should <= count of global, all we care is when local < global happens.
The difference between local and global is global also include non-adjacent i and j. So for every i, find in range 0 to i-2, see if there is an element which is larger than A[i]. We can maintain a variable max for the linear implementation.
public static boolean isIdealPermutation(int[] A) {
int max = -1;
for (int i = 0; i < A.length - 2; i++) {
max = Math.max(max, A[i]);
if (max > A[i + 2])
return false;
}
return true;
}
- Count inversions
Design an efficient algorithm that takes an array of integers and returns the number of inverted pairs of indices.
Solution:
The brute-force algorithm examines all pairs of indices, has an O(n^2) complexity.
Suppose we split the array A to left half L and the right half R. Sorting L and R makes it possible to efficiently count: For any (i,j) pair where i is an index in L and j is an index in R, if L[i] > R[j], then for all j’ < j we must have L[i] > R[j’].
The time complexity satisfies T(n) = O(n) + 2T(n-1), which solves to O(nlogn).
public static int countInversions(List<Integer> nums) {
return countInversions(nums, 0, nums.size() - 1);
}
private static int countInversions(List<Integer> nums, int low, int high) {
if (low >= high)
return 0;
int mid = low + (high - low) / 2;
int count = countInversions(nums, low, mid); // exclude mid
count += countInversions(nums, mid + 1, high); // include mid
count += mergeSortAndCountInversions(nums, low, mid, high);
return count;
}
/**
* Merge two sorted sublists and count inversions across the two sublists.
*/
private static int mergeSortAndCountInversions(List<Integer> nums, int low, int mid, int high) {
List<Integer> sortedNums = new ArrayList<>();
int l = low, h = mid + 1, count = 0;
while (l <= mid && h <= high) {
if (Integer.compare(nums.get(l), nums.get(h)) <= 0) {
sortedNums.add(nums.get(l++));
} else {
// nums[leftStart, mid) are the inversions of nums[rightStart]
count += mid - l;
sortedNums.add(nums.get(h++));
}
}
// add all the rest items
sortedNums.addAll(nums.subList(l, mid));
sortedNums.addAll(nums.subList(h, high));
// update with sorted list
for (Integer num : sortedNums) {
nums.set(low++, num);
}
return count;
}
Draw The Skyline
A number of buildings are visible from a point. A building appears as a rectangle, with the bottom of each building lying on a fixed horizontal line.
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height.
For instance, the dimensions of all buildings in Figure A are recorded as: [[2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8]].
The skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Design an efficient algorithm for computing the skyline.
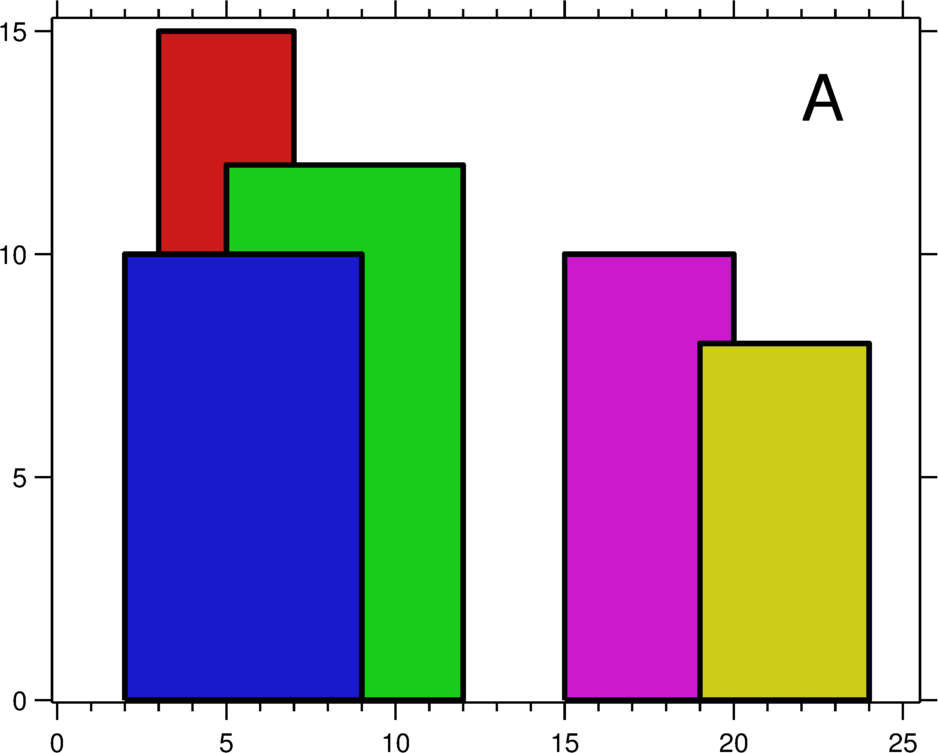 |
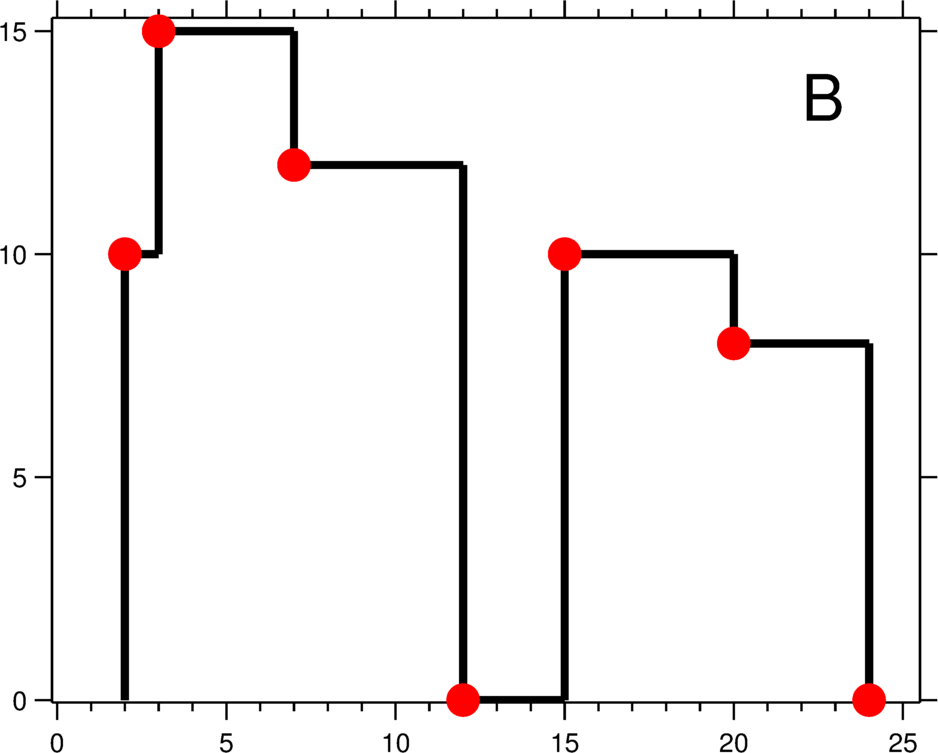 |
Solution:
Scan across the critical points from left to right:
- When we encounter the left edge of a rectangle, we add this rectangle to the heap with its height as the key.
- When we encounter the right edge of a rectangle, we remove this height from the heap.
- Any time we encounter a critical point, after updating the heap, we set the height of that critical point to the value peeked from the top of the heap.
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> result = new ArrayList<>();
List<int[]> heights = new ArrayList<>();
for (int[] building : buildings) {
heights.add(new int[] { building[0], -building[2] });
heights.add(new int[] { building[1], building[2] });
}
Collections.sort(heights, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]));
Queue<Integer> queue = new PriorityQueue<>((a, b) -> (b - a));
queue.offer(0);
int prev = 0;
for (int[] height : heights) {
if (height[1] < 0)
queue.offer(-height[1]);
else
queue.remove(height[1]);
int curr = queue.peek();
if (curr != prev) {
result.add(new int[] { height[0], curr });
prev = curr;
}
}
return result;
}
// use tree map
public List<int[]> getSkyline2(int[][] buildings) {
int minLeft = Integer.MAX_VALUE, maxRight = Integer.MIN_VALUE;
for (int[] building : buildings) {
minLeft = Math.min(minLeft, building[0]);
maxRight = Math.max(maxRight, building[1]);
}
int[] heights = new int[maxRight - minLeft + 1];
for (int[] building : buildings) {
for (int i = building[0]; i <= building[1]; i++) {
heights[i - minLeft] = Math.max(heights[i - minLeft], building[2]);
}
}
List<int[]> result = new ArrayList<>();
int left = 0;
for (int i = 1; i < heights.length; i++) {
if (heights[i] != heights[i - 1]) {
result.add(new int[] { left + minLeft, i - 1 + minLeft, heights[i - 1] });
left = i;
}
}
result.add(new int[] { left + minLeft, maxRight, heights[heights.length - 1] });
return result;
}
Keep City Skyline
In a 2 dimensional array grid, each value grid[i][j] represents the height of a building located there. We are allowed to increase the height of any number of buildings, by any amount (the amounts can be different for different buildings). Height 0 is considered to be a building as well.
At the end, the “skyline” when viewed from all four directions of the grid, i.e. top, bottom, left, and right, must be the same as the skyline of the original grid. A city’s skyline is the outer contour of the rectangles formed by all the buildings when viewed from a distance. See the following example.
What is the maximum total sum that the height of the buildings can be increased?
Example:
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation:
The grid is:
[ [3, 0, 8, 4],
[2, 4, 5, 7],
[9, 2, 6, 3],
[0, 3, 1, 0] ]
The skyline viewed from top or bottom is: [9, 4, 8, 7]
The skyline viewed from left or right is: [8, 7, 9, 3]
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
public int maxIncreaseKeepingSkyline(int[][] grid) {
int n = grid.length;
int[] col = new int[n], row = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
row[i] = Math.max(row[i], grid[i][j]);
col[j] = Math.max(col[j], grid[i][j]);
}
}
int result = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
result += Math.min(row[i], col[j]) - grid[i][j];
return result;
}
Optimal Account Balancing
You are given an array of transactions transactions where transactions[i] = [from, to, amount] indicates that the person with ID = from gave amount $ to the person with ID = to.
Return the minimum number of transactions required to settle the debt.
Example:
Input: transactions = [[0,1,10],[1,0,1],[1,2,5],[2,0,5]]
Output: 1
Explanation:
Person #0 gave person #1 $10.
Person #1 gave person #0 $1.
Person #1 gave person #2 $5.
Person #2 gave person #0 $5.
Therefore, person #1 only need to give person #0 $4, and all debt is settled.
public int minTransfers(int[][] transactions) {
// Sum up each account's balance
Map<Integer, Integer> balanceMap = new HashMap<>();
for (int[] transaction : transactions) {
balanceMap.put(transaction[0], balanceMap.getOrDefault(transaction[0], 0) + transaction[2]);
balanceMap.put(transaction[1], balanceMap.getOrDefault(transaction[1], 0) - transaction[2]);
}
// Need a list here, able to get value at specific index
// Just need a balance list as account ids are irrelevant
List<Integer> balanceList = new ArrayList<>();
balanceList.addAll(balanceMap.values());
// Map the indices of balances for quick lookup to prune
Map<Integer, TreeSet<Integer>> balanceToIdxMap = new HashMap<>();
for (int i = 0; i < balanceList.size(); i++) {
balanceToIdxMap.computeIfAbsent(balanceList.get(i), k -> new TreeSet<>()).add(i);
}
return backTrackTransactions(balanceList, 0, balanceToIdxMap);
}
private int backTrackTransactions(List<Integer> balanceList, int position, Map<Integer, TreeSet<Integer>> balanceToIdxMap) {
if (position == balanceList.size())
return 0;
int currBalance = balanceList.get(position);
// Skip zero balance and proceed with next one
if (currBalance == 0)
return backTrackTransactions(balanceList, position + 1, balanceToIdxMap);
// Look for lowest index that is higher than current position, but has the opposite balance.
int nextBalance = -currBalance;
if (balanceToIdxMap.containsKey(nextBalance)) {
TreeSet<Integer> set = balanceToIdxMap.get(nextBalance);
Integer idx = set.ceiling(position); // lowest index
if (idx != null) {
set.remove(idx);
balanceList.set(idx, 0);
int transactions = backTrackTransactions(balanceList, position + 1, balanceToIdxMap) + 1;
set.add(idx);
balanceList.set(idx, nextBalance);
return transactions;
}
}
// Otherwise, go through the rest of the list if not found an optimal balance
int minTransactions = balanceList.size() - 1; // max transactions
for (int i = position + 1; i < balanceList.size(); i++) {
nextBalance = balanceList.get(i);
if (nextBalance * currBalance >= 0)
continue; // Skip for the same side
balanceList.set(i, currBalance + nextBalance);
int transactions = backTrackTransactions(balanceList, position + 1, balanceToIdxMap) + 1;
balanceList.set(i, nextBalance);
minTransactions = Math.min(minTransactions, transactions);
}
return minTransactions;
}
Analyze User Website Visit Pattern
/**
* You are given two string arrays username and website and an integer array timestamp. All the
* given arrays are of the same length and the tuple [username[i], website[i], timestamp[i]]
* indicates that the user username[i] visited the website website[i] at time timestamp[i].
*
* A pattern is a list of three websites (not necessarily distinct).
*
* For example, ["home", "away", "love"], ["leetcode", "love", "leetcode"], and ["luffy", "luffy",
* "luffy"] are all patterns. The score of a pattern is the number of users that visited all the
* websites in the pattern in the same order they appeared in the pattern.
*
* For example, if the pattern is ["home", "away", "love"], the score is the number of users x such
* that x visited "home" then visited "away" and visited "love" after that. Similarly, if the
* pattern is ["leetcode", "love", "leetcode"], the score is the number of users x such that x
* visited "leetcode" then visited "love" and visited "leetcode" one more time after that. Also, if
* the pattern is ["luffy", "luffy", "luffy"], the score is the number of users x such that x
* visited "luffy" three different times at different timestamps. Return the pattern with the
* largest score. If there is more than one pattern with the same largest score, return the
* lexicographically smallest such pattern.
*
*
* <pre>
* Example 1:
*
* Input: username = ["joe","joe","joe","james","james","james","james","mary","mary","mary"], timestamp = [1,2,3,4,5,6,7,8,9,10], website = ["home","about","career","home","cart","maps","home","home","about","career"]
* Output: ["home","about","career"]
* Explanation: The tuples in this example are:
* ["joe","home",1],["joe","about",2],["joe","career",3],["james","home",4],["james","cart",5],["james","maps",6],["james","home",7],["mary","home",8],["mary","about",9], and ["mary","career",10].
* The pattern ("home", "about", "career") has score 2 (joe and mary).
* The pattern ("home", "cart", "maps") has score 1 (james).
* The pattern ("home", "cart", "home") has score 1 (james).
* The pattern ("home", "maps", "home") has score 1 (james).
* The pattern ("cart", "maps", "home") has score 1 (james).
* The pattern ("home", "home", "home") has score 0 (no user visited home 3 times).
* </pre>
*
*
* https://leetcode.com/problems/analyze-user-website-visit-pattern/
*
*/
public class UserWebsiteVisitPattern {
public List<String> mostVisitedPattern(String[] usernames, int[] timestamps, String[] websites) {
Queue<int[]> queue = new PriorityQueue<>((a, b) -> a[0] - b[0]);
for (int i = 0; i < timestamps.length; i++) {
queue.offer(new int[] { timestamps[i], i });
}
Node root = new Node();
while (!queue.isEmpty()) {
int i = queue.poll()[1];
// Add all to root first!
root.usernames.add(usernames[i]);
root.add(usernames[i], websites[i]);
}
Node current = root;
List<String> result = new ArrayList<>();
// Get the max website on each level
while (!current.children.isEmpty()) {
int maxCount = 0;
String maxWebsite = "";
for (Map.Entry<String, Node> entry : current.children.entrySet()) {
Node node = entry.getValue();
if (node.count > maxCount || (node.count == maxCount && entry.getKey().compareTo(maxWebsite) < 0)) {
maxCount = node.count;
maxWebsite = entry.getKey();
current = node;
}
}
result.add(maxWebsite);
}
return result;
}
private class Node {
Map<String, Node> children;
Set<String> usernames;
int count;
int level;
public Node() {
children = new HashMap<>();
usernames = new HashSet<>();
}
public int add(String username, String website) {
if (!usernames.contains(username)) {
return 0;
}
// Bottom up and try to all 3 levels if applicable
if (level < 2) {
for (String key : children.keySet()) {
count = Math.max(count, children.get(key).add(username, website));
}
}
Node childNode = null;
// Add to website node if not exists
if (!children.containsKey(website)) {
childNode = new Node();
childNode.level = level + 1;
children.put(website, childNode);
}
// Add to user names if not exists
childNode = children.get(website);
if (!childNode.usernames.contains(username)) {
if (childNode.level == 3) {
// This username reached here the first time
childNode.count++;
}
childNode.usernames.add(username);
}
// Update level 2's count and up
if (childNode.level == 3) {
count = Math.max(count, childNode.count);
}
return count;
}
}
}
Product Questions
Maximum Product of Three
Given an integer array, find three numbers whose product is maximum and output the maximum product.
For example: if A = [1, 2, 3, 4], the result is 24.
Solution:
We only need to find the required 2 smallest values(min1 and min2) and the three largest values(max1, max2, max3) in one loop.
public int maximumProductOfThree(int[] nums) {
int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE, min1 = Integer.MAX_VALUE,
min2 = Integer.MAX_VALUE;
for (int n : nums) {
if (n > max1) {
max3 = max2;
max2 = max1;
max1 = n;
} else if (n > max2) {
max3 = max2;
max2 = n;
} else if (n > max3) {
max3 = n;
}
if (n < min1) {
min2 = min1;
min1 = n;
} else if (n < min2) {
min2 = n;
}
}
return Math.max(max1 * max2 * max3, max1 * min1 * min2);
}
Maximum Product Subarray
Find the contiguous subarray within an array (containing at least one number) which has the largest product.
For example, given the array [2,3,-2,4], the contiguous subarray [2,3] has the largest product = 6.
Solution:
public static int maxProductOfSubarray(int[] nums) {
int maxSoFar = nums[0];
int iMax = maxSoFar, iMin = maxSoFar;
// starts from 1!
for (int i = 1; i < nums.length; i++) {
// swap them if multiplied by a negative
if (nums[i] < 0) {
int temp = iMin;
iMin = iMax;
iMax = temp;
}
iMax = Math.max(nums[i], iMax * nums[i]);
iMin = Math.min(nums[i], iMin * nums[i]);
maxSoFar = Math.max(maxSoFar, iMax);
}
return maxSoFar;
}
Maximum Product Except Self
Also called Product of Array Except Self
Given an array nums of n integers where n > 1, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].
Example: Input: [1,2,3,4], Output: [24,12,8,6]
public int[] productExceptSelf(int[] nums) {
int[] res = new int[nums.length];
int left = 1;
for (int i = 0; i < nums.length; i++) {
res[i] = left;
left *= nums[i];
}
int right = 1;
for (int i = nums.length - 1; i >= 0; i--) {
res[i] *= right;
right *= nums[i];
}
return res;
}
Maximum Product Except One
Given an array A of length n whose entries are integers, compute the largest product that can made using n - 1 entries in A. Array entries may be positive, negative or 0.
For example: if A = {3, 2, -1, 4, -1, 6}, the result is 3 * -1 * 4 * -1 * 6 = 72.
Solution:
If the number of negative entries is odd, the maximum product uses all numbers except the least negative entry; if the number of negative entries is even, should exclude the least nonnegative entry, but if there are no nonnegative entry, let’s exclude the greatest negative entry.
public static int maxProductExceptOne(int[] nums) {
int numOfNegatives = 0;
int leastNegativeIdx = -1, leastNonNegativeIdx = -1, greatestNegativeIdx = -1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] < 0) {
numOfNegatives++;
if (leastNegativeIdx == -1 || nums[i] > nums[leastNegativeIdx]) {
leastNegativeIdx = i;
}
if (greatestNegativeIdx == -1 || nums[i] < nums[greatestNegativeIdx]) {
greatestNegativeIdx = i;
}
} else {
if (leastNonNegativeIdx == -1 || nums[i] < nums[leastNonNegativeIdx]) {
leastNonNegativeIdx = i;
}
}
}
int idxToSkip = numOfNegatives % 2 == 0
? (leastNonNegativeIdx == -1 ? greatestNegativeIdx : leastNonNegativeIdx) : leastNegativeIdx;
int product = 1;
for (int i = 0; i < nums.length; i++) {
if (i != idxToSkip)
product *= nums[i];
}
return product;
}
Maximum Product Less Than K
Given an array of positive integers numbers. Count and print the number of (contiguous) subarrays where the product of all the elements in the subarray is less than k.
For example:
Input: nums = [10, 5, 2, 6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6].
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.
Solution:
We can use sliding window, keep tracking prod = nums[left] * nums[left + 1] * ... * nums[right] is less than k. For every right, we update left and prod to maintain this invariant. Also we count in right - left + 1.
public static int numSubarrayProductLessThanK(int[] nums, int k) {
if (k <= 1) // must be greater than 1
return 0;
int prod = 1, left = 0, result = 0;
for (int right = 0; right < nums.length; right++) {
prod *= nums[right];
while (prod >= k) {
prod /= nums[left++];
}
result += right - left + 1;
}
return result;
}
Count Smaller Numbers After Self
You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].
Example:
Input: [5,2,6,1]
Output: [2,1,1,0]
Explanation:
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.
Solution 1: Traverse Backward with Binary Search, Complexity: O(nlog(n))
public List<Integer> countSmaller(int[] nums) {
List<Integer> ans = new LinkedList<>(); // only insert
List<Integer> visited = new ArrayList<>(); // sorted binary search array
for (int i = nums.length - 1; i >= 0; i--) {
int count = getIndex(visited, nums[i]);
if (count < visited.size()) {
visited.add(count, nums[i]); // O(n)
} else {
visited.add(nums[i]);
}
ans.add(0, count);
}
return ans;
}
private int getIndex(List<Integer> visited, int target) {
if (visited.isEmpty())
return 0;
int start = 0, end = visited.size();
while (start < end) {
int mid = start + (end - start) / 2;
if (visited.get(mid) < target) {
start = mid + 1;
} else {
end = mid;
}
}
return end;
}
Solution 2: Use Binary Indexed Tree over Segment, Complexity: O(nlog(n)), but efficient due to array operations.
// Use num value as index, and always +1 for prefix sum
public List<Integer> countSmaller(int[] nums) {
if (nums.length == 0)
return new ArrayList<>();
Integer[] ans = new Integer[nums.length];
int min = Integer.MAX_VALUE;
for (int i = 0; i < nums.length; i++) {
min = Math.min(min, nums[i]);
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
// Let index starts from 1
nums[i] = nums[i] - min + 1;
max = Math.max(max, nums[i]);
}
// build a binary indexed tree
int[] tree = new int[max + 1];
for (int i = nums.length - 1; i >= 0; i--) {
ans[i] = getCount(nums[i] - 1, tree); // smaller numbers
updateCount(nums[i], tree);
}
return Arrays.asList(ans);
}
// O(log(n))
private void updateCount(int idx, int[] tree) {
while (idx < tree.length) {
tree[idx]++;
idx += (idx & -idx); // plus right most set bit to get parents
}
}
// O(log(n))
private int getCount(int idx, int[] tree) {
int count = 0;
while (idx > 0) {
count += tree[idx];
idx -= (idx & -idx); // minus right most set bit to get children
}
return count;
}
Subarray Questions
Longest Continuous Increasing
Given an unsorted array of integers, find the length of longest continuous increasing subsequence (subarray).
For example, if A = [1,3,5,4,7], The longest continuous increasing subsequence is [1,3,5], its length is 3.
Solution:
For the continuous subarray issue, we can first consider using sliding window. As below, we can use an anchor to mark the start of a new increasing subsequence at nums[i].
public static int[] longestContinuousIncreasingSubarray(int[] nums) {
int start = 0, end = 0;
int max = 0, anchor = 0;
for (int i = 0; i < nums.length; i++) {
if (i > 0 && nums[i - 1] >= nums[i])
anchor = i;
if (max < i - anchor + 1) {
max = i - anchor + 1;
start = anchor;
end = i;
}
}
return new int[] { start, end };
}
Continuous Subarray Sum
Given a list of non-negative numbers and a target integer k, write a function to check if the array has a continuous subarray of size at least 2 that sums up to the multiple of k, that is, sums up to n*k where n is also an integer.
For example: if A = [1, 23, 2, 6, 4, 7, 9] and k = 6, because [23, 2, 6, 4, 7] is an continuous subarray of size 5 and sums up to 42, which is the multiple of 6.
Solution:
We make use of a hash map to store the modulus (with given k) of the the cumulative sums up to ith along with index. During traverse if we find another jth whose modulus equals to ith. we can calculate the size = j - i + 1.
public static boolean continousSubarraySum(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
map.put(0, -1);
int runningSum = 0;
for (int i = 0; i < nums.length; i++) {
runningSum += nums[i];
if (k != 0)
runningSum %= k;
if (map.containsKey(runningSum)) {
if (i - map.get(runningSum) > 1)
return true;
} else
map.put(runningSum, i);
}
return false;
}
Subarray Sums Divisible by K
Given an integer array nums and an integer k, return the number of non-empty subarrays that have a sum divisible by k.
A subarray is a contiguous part of an array.
Example 1:
Input: nums = [4,5,0,-2,-3,1], k = 5; Output: 7
Explanation: There are 7 subarrays with a sum divisible by k = 5: [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
public int subarraysDivByK(int[] nums, int K) {
if (nums == null || nums.length == 0 || K == 0)
return 0;
int ans = 0, sum = 0, remainder;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1); // 0 as remainder to be 1
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
remainder = sum % K;
if (remainder < 0)
remainder += K; // convert to positive
if (map.containsKey(remainder)) {
ans += map.get(remainder);
}
map.put(remainder, map.getOrDefault(remainder, 0) + 1);
}
return ans;
}
Maximum Subarray Sum
Find the contiguous subarray within an array (containing at least one number) which has the largest sum.
For example, given the array [-2,1,-3,4,-1,2,1,-5,4], the contiguous subarray [4,-1,2,1] has the largest sum = 6.
Solution:
public static int maxSubArraySum(int[] nums) {
int max = Integer.MIN_VALUE, sum = 0;
for (int i = 0; i < nums.length; i++) {
// break point if sum <= 0
sum = Math.max(nums[i], sum + nums[i]);
max = Math.max(max, sum);
}
return max;
}
Maximum Subarray Sum Equals K
Given an array nums and a target value k, find the maximum length of a subarray that sums to k. If there isn’t one, return 0 instead.
Note: The sum of the entire nums array is guaranteed to fit within the 32-bit signed integer range.
Example 1: Given nums = [1, -1, 5, -2, 3], k = 3, return 4. (because the subarray [1, -1, 5, -2] sums to 3 and is the longest)
Solution:
The HashMap stores the sum of all elements before index i as key, and i as value. For each i, check not only the current sum but also (currentSum - previousSum) to see if there is any that equals k, and update max length.
// Just need to adjust: Subarray Sum Equals K
public int subarraySumEqualsK(int[] nums, int k) {
int count = 0, sum = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
if (map.containsKey(sum - k))
count += map.get(sum - k);
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return count;
}
public int maxSubArraySumEqualsK(int[] nums, int k) {
int sum = 0, max = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
sum = sum + nums[i];
if (sum == k)
max = i + 1;
else if (map.containsKey(sum - k))
max = Math.max(max, i - map.get(sum - k));
if (!map.containsKey(sum))
map.put(sum, i);
}
return max;
}
Maximum Subarray Sum <= K
Design an algorithm that takes as input an array A of n numbers and a key k, and return the length of a longest subarray of A for which the subarray sum is less than or equal to k.
Solution:
First build the min prefix sum, then let a <= b be indices of elements in A. Navigate a, b to satisfying the sum constraint, and track the max length.
public static int maxSubArraySumLessEqualsK(int[] nums, int k) {
// build the prefix sum
int[] prefixSum = new int[nums.length];
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
prefixSum[i] = sum;
}
// early returns if sum <= k
if (prefixSum[nums.length - 1] <= k)
return nums.length;
// build the min prefix sum
int[] minPrefixSum = Arrays.copyOf(prefixSum, prefixSum.length);
for (int i = nums.length - 2; i >= 0; i--) {
minPrefixSum[i] = Math.min(minPrefixSum[i], minPrefixSum[i + 1]);
}
// minPrefixSum[b] - prefixSum[a - 1]
int a = 0, b = 0, maxLen = 0;
while (a < nums.length && b < nums.length) {
int minCurSum = a == 0 ? minPrefixSum[b] : minPrefixSum[b] - prefixSum[a - 1];
if (minCurSum <= k) {
int curLen = b - a + 1;
maxLen = Math.max(maxLen, curLen);
b++;
} else {
a++;
}
}
return maxLen;
}
Array Questions
Circular Array Loop
You are given an array of positive and negative integers. If a number n at an index is positive, then move forward n steps. Conversely, if it’s negative (-n), move backward n steps. Assume the first element of the array is forward next to the last element, and the last element is backward next to the first element. Determine if there is a loop in this array. A loop starts and ends at a particular index with more than 1 element along the loop. The loop must be “forward” or “backward’.
Example 1: Given the array [2, -1, 1, 2, 2], there is a loop, from index 0 -> 2 -> 3 -> 0.
Example 2: Given the array [-1, 2], there is no loop.
Solution: Use slow and fast pointers.
public static boolean circularArrayLoop(int[] nums) {
if (nums.length <= 1) {
return false; // edge scenario checking
}
for (int i = 0; i < nums.length; i++) {
// no movement
if (nums[i] == 0) {
continue;
}
int slow = i, fast = getNext(nums, i);
// with the same direction, both negative or positive!
while (nums[slow] * nums[fast] > 0 && nums[fast] * nums[getNext(nums, fast)] > 0) {
if (slow == fast) {
// check for loop with only one element
if (slow == getNext(nums, slow)) {
break;
}
return true;
}
slow = getNext(nums, slow);
fast = getNext(nums, getNext(nums, fast));
}
// loop not found, set all elements along the way to 0
int curr = i, value = nums[i];
while (nums[curr] * value > 0) {
int next = getNext(nums, curr);
nums[curr] = 0;
curr = next;
}
}
return false;
}
private static int getNext(int[] nums, int i) {
int n = nums.length, x = i + nums[i];
return x % n + (x >= 0 ? 0 : n);
}
Compute Fair Bonus
Write a program for computing the minimum number of tickets to distribute to the developers, while ensuring that if a developer has written more lines of code than a neighbor, then he receives more tickets than his neighbor.
Solution:
We can use a min-heap (O(nlogn)), but a total ordering on the developers is overkill, since the specified constraint is very local. Indeed, we can improve the time complexity to O(n) by making two passes over the array.
public static int calculateBonus(int[] productivity) {
int[] tickets = new int[productivity.length];
Arrays.fill(tickets, 1);
// from left to right
for (int i = 1; i < productivity.length; i++) {
if (productivity[i] > productivity[i - 1])
tickets[i] = tickets[i - 1] + 1;
}
// from right to left
for (int i = productivity.length - 2; i >= 0; i--) {
if (productivity[i] > productivity[i + 1]) {
tickets[i] = Math.max(tickets[i], tickets[i + 1] + 1);
}
}
return Arrays.stream(tickets).sum();
}
Search Unbound Array
Design an algorithm that takes a sorted array whose length is not know, and a key, and returns an index of an array element which is equal to the key. Assume that an out-of-bounds access throws an exception.
Solution:
We can compute the array length by testing whether indices \(0, 1, 3, 7, 15,...2^i - 1\) are valid. As soon as we found the value of index \(2^i - 1\) is greater than the key or reached the invalid index, say \(2^i - 1\), we can use binary search over the interval \([2^{i-1}, 2^i - 2]\) for the key. 2 loops both have O(log(n)) complexity.
public static int searchUnboundArray(int[] array, int key) {
// find a range where key exists if it's present
int p = 0;
while (true) {
try {
int idx = (1 << p) - 1;
if (array[idx] == key) {
return idx;
} else if (array[idx] > key) {
break;
}
} catch (IndexOutOfBoundsException e) {
break;
}
p++;
}
// binary search between indices 2^(p-1) and 2^p - 2, inclusive
int left = Math.max(0, 1 << (p - 1)), right = (1 << p) - 2;
while (left <= right) {
int mid = left + (right - left) / 2;
try {
if (array[mid] == key) {
return mid;
} else if (array[mid] > key) {
right = mid - 1;
} else {
left = mid + 1;
}
} catch (IndexOutOfBoundsException e) {
right = mid - 1;
}
}
return -1; // nothing matched!
}
Find Kth Largest Element
Design an algorithm for computing the kth largest element in a sequence of elements.
Solution:
Track the k largest elements, but don’t update the collection immediately after each new element is read.
By using 2k - 1 as the array size, the time complexity to find the kth largest element is almost certain O(k), it runs every k - 1 elements, implying an O(n) time complexity.
We could use less storage, e.g., an array of length 3k/2, and still achieve O(n) time complexity. This is a classic space-time trade-off. If we use a 4k long array, we could discard 3k elements for one call to findKthLargest, which is proportional to the length of the array.
public static int findKthLargestUnknownLength(Iterator<Integer> stream, int k) {
int size = 2 * k - 1; // the bigger the more efficient! but use more space
List<Integer> candidates = new ArrayList<>(size);
while (stream.hasNext()) {
candidates.add(stream.next());
if (candidates.size() == size) {
findKthLargest(candidates, 0, candidates.size() - 1, k);
candidates.subList(k, candidates.size()).clear();
}
}
findKthLargest(candidates, 0, candidates.size() - 1, k);
return candidates.get(k - 1);
}
private static int findKthLargest(List<Integer> nums, int start, int end, int k) {
if (start > end)
return Integer.MAX_VALUE;
int left = start;
// Pick the last value as pivot or randomize a pivot index and swap with the end index.
int pivot = nums.get(end);
for (int i = start; i <= end; i++) {
if (nums.get(i) > pivot) {
Collections.swap(nums, left++, i);
}
}
Collections.swap(nums, left, end);
if (left == k - 1)
return nums.get(left);
else if (left < k - 1)
return findKthLargest(nums, left + 1, end, k);
else
return findKthLargest(nums, start, left - 1, k);
}
Max Sum in Circular Array
Given a circular array A, compute its maximum subarray sum in O(n) time.
Solution:
-
We compute for each i the maximum subarray sum Si for the subarray that starts at 0 and ends at or before i, and the maximum subarray Ei for the subarray that starts after i and ends at the last element. Then the maximum subarray sum for a subarray that cycles around is the maximum over all i of Si + Ei.
-
The maximum subarray may or may not cycle around. The maximum subarray that cycles around can be determined by computing the minimum subarray – the remaining elements yield a subarray that cycles around. This approach uses O(1) space and O(n) time complexity.
public static int maxSubarraySumInCircular(List<Integer> A) {
int accumulate = 0;
for (int a : A) {
accumulate += a;
}
return Math.max(findOptimumSubarraySum(A, new MaxComparator()),
accumulate - findOptimumSubarraySum(A, new MinComparator()));
}
private static int findOptimumSubarraySum(List<Integer> A, Comparator<Integer> compator) {
int till = 0, overall = 0;
for (int a : A) {
till = compator.compare(a, a + till);
overall = compator.compare(overall, till);
}
return overall;
}
private static class MaxComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o1 > o2 ? o1 : o2;
}
}
private static class MinComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o1 > o2 ? o2 : o1;
}
}
List & BST
Sorted Singly List to BST
Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
Solution:
O(n) time complexity and O(logn) space complexity.
public TreeNode sortedSinglyListToBST(ListNode head) {
if (head == null)
return null;
return sortedSinglyListToBST(head, null);
}
private TreeNode sortedSinglyListToBST(ListNode head, ListNode tail) {
if (head == tail)
return null;
ListNode slow = head, fast = head;
while (fast != tail && fast.next != tail) {
slow = slow.next;
fast = fast.next.next;
}
TreeNode root = new TreeNode(slow.val);
root.left = sortedSinglyListToBST(head, slow);
root.right = sortedSinglyListToBST(slow.next, tail);
return root;
}
Sorted Doubly List to BST
Given a doubly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
Solution:
// must use a global head anchor track the current location!
private ListNode headAnchor;
public ListNode sortedDLLToBalancedBST(ListNode head) {
if (head == null)
return null;
// caculate length of list
int length = 0;
ListNode node = head;
while (node != null) {
length++;
node = node.next;
}
this.headAnchor = head;
return sortedDLLToBalancedBST(0, length);
}
private ListNode sortedDLLToBalancedBST(int start, int end) {
if (start >= end)
return null;
int mid = start + (end - start) / 2;
ListNode left = sortedDLLToBalancedBST(start, mid);
ListNode curr = new ListNode(headAnchor.val, left, null);
headAnchor = headAnchor.next;
curr.next = sortedDLLToBalancedBST(mid + 1, end);
return curr;
}
BST to Circular Sorted DLL
// Transform a BST into a circular sorted DLL with Postorder traversal!
// Circular DLL makes it easier to track head and tail
// left subtree + node + right subtree -> make it circular
public TreeNode balancedBSTToSortedDLL(TreeNode node) {
if (node == null)
return null;
TreeNode lHead = balancedBSTToSortedDLL(node.left);
TreeNode rHead = balancedBSTToSortedDLL(node.right);
// append node to the list from the left subtree
TreeNode lTail = null;
if (lHead != null) {
lTail = lHead.left;
lTail.right = node; // Add node after lTail
node.left = lTail; // Double link it
lTail = node; // Update lTail to node
} else {
lHead = lTail = node;
}
// append the list from right substree to node
TreeNode rTail = null;
if (rHead != null) {
rTail = rHead.left;
lTail.right = rHead; // Add rHead after lTail
rHead.left = lTail; // Double link it
} else {
rTail = lTail;
}
// make it circular
rTail.right = lHead;
lHead.left = rTail;
return lHead;
}
// Transform a BST into a circular sorted DLL with Inorder traversal!
// Circular DLL makes it easier to track head and tail
// left subtree + node + right subtree -> make it circular
TreeNode head = null, tail = null;
public TreeNode treeToDoublyList(TreeNode node) {
if (node == null)
return null;
treeToDoublyList(node.left);
if (tail != null) {
tail.right = node; // link node after rTail
node.left = tail;
} else {
head = node; // keep the smallest as head
}
tail = node;
treeToDoublyList(node.right);
// Make it circular
tail.right = head;
head.left = tail;
return head;
}
Merge Two BSTs
Given two balanced binary search tree. Write a function that merges them into a balance binary search tree.
Solution:
Method 1: Insert elements of the bigger tree into the smaller tree. So time complexity of this method is Log(n) + Log(n+1) + … + Log(n+m-1). Which is between mLog(n) and mLog(m+n-1).
Method 2: Merge inorder traversal, do inorder traversal of the two trees and store into two arrays, merge the two arrays into one array which can be used to construct the merged BST. The time and space complexity are both O(m+n).
Method 3: In-place merge using DDL, convert the two trees into doubly linked list in place, merge the two DLLs which will be used to build the BST. The time complexity is still O(m+n), but space complexity is O(h) where h is the maximum height of the two initial trees (stack depth).
public TreeNode mergeTwoBSTs(TreeNode treeA, TreeNode treeB) {
treeA = balancedBSTToSortedDLL(treeA);
treeB = balancedBSTToSortedDLL(treeB);
// break the circular first!
treeA.left.right = null;
treeB.left.right = null;
treeA.left = null;
treeB.left = null;
return sortedListToBalancedBST(mergeTwoSortedDLLs(treeA, treeB));
}
private TreeNode headPointer = null;
// Not required to be DLL
private TreeNode sortedListToBalancedBST(TreeNode node) {
headPointer = node;
return sortedListToBalancedBST(0, countLength(node));
}
// Use Inorder traversal with a head pointer
private TreeNode sortedListToBalancedBST(int start, int end) {
if (start >= end)
return null;
int mid = start + (end - start) / 2;
TreeNode left = sortedListToBalancedBST(start, mid);
TreeNode curr = new TreeNode(headPointer.val, left, null);
headPointer = headPointer.right;
curr.right = sortedListToBalancedBST(mid + 1, end);
return curr;
}
// Return sorted linked list (not neccessary to be DLL)
private TreeNode mergeTwoSortedDLLs(TreeNode A, TreeNode B) {
TreeNode dummyHead = new TreeNode();
TreeNode current = dummyHead;
TreeNode p1 = A, p2 = B;
while (p1 != null && p2 != null) {
if (Integer.compare(p1.val, p2.val) < 0) {
current.right = p1;
p1 = p1.right;
} else {
current.right = p2;
p2 = p2.right;
}
current = current.right;
}
if (p1 != null) {
current.right = p1;
}
if (p2 != null) {
current.right = p2;
}
return dummyHead.right;
}
private static int countLength(TreeNode node) {
int len = 0;
while (node != null) {
len++;
node = node.right;
}
return len;
}
If it’s to simply merge the counterparts as below: The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.
Input:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
Output:
Merged tree:
3
/ \
4 5
/ \ \
5 4 7
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null)
return null;
int mergedValue = (t1 == null ? 0 : t1.val) + (t2 == null ? 0 : t2.val);
TreeNode newNode = new TreeNode(mergedValue);
newNode.left = mergeTrees(t1 == null ? null : t1.left, t2 == null ? null : t2.left);
newNode.right = mergeTrees(t1 == null ? null : t1.right, t2 == null ? null : t2.right);
return newNode;
}
Accounts Merge
Given a list of accounts where each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account.
Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some common email to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name.
After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.
Example 1:
Input: accounts = [[“John”,”johnsmith@mail.com”,”john_newyork@mail.com”],[“John”,”johnsmith@mail.com”,”john00@mail.com”],[“Mary”,”mary@mail.com”],[“John”,”johnnybravo@mail.com”]] Output: [[“John”,”john00@mail.com”,”john_newyork@mail.com”,”johnsmith@mail.com”],[“Mary”,”mary@mail.com”],[“John”,”johnnybravo@mail.com”]] Explanation: The first and third John’s are the same person as they have the common email “johnsmith@mail.com”. The second John and Mary are different people as none of their email addresses are used by other accounts. We could return these lists in any order, for example the answer [[‘Mary’, ‘mary@mail.com’], [‘John’, ‘johnnybravo@mail.com’], [‘John’, ‘john00@mail.com’, ‘john_newyork@mail.com’, ‘johnsmith@mail.com’]] would still be accepted.
Solution: Disjoint Set Union (DSU) or Depth-First Search (DFS) Time Complexity: O(AlogA),where A=∑ai and ai is the length of accounts[i]
public List<List<String>> accountsMergeWithDSU(List<List<String>> accounts) {
DSU dsu = new DSU();
Map<String, String> emailToName = new HashMap<>();
Map<String, Integer> emailToID = new HashMap<>();
int id = 0;
for (List<String> account : accounts) {
String name = null;
for (String email : account) {
if (name == null) {
name = email;
continue;
}
emailToName.put(email, name);
if (!emailToID.containsKey(email)) {
emailToID.put(email, id++);
}
dsu.union(emailToID.get(account.get(1)), emailToID.get(email));
}
}
// Add all union emails
Map<Integer, List<String>> ans = new HashMap<>();
emailToID.forEach((email, id2) ->
{
ans.computeIfAbsent(dsu.find(id2), x -> new ArrayList<>()).add(email);
});
// Add name to the first place
for (List<String> component : ans.values()) {
Collections.sort(component); // Sort emails first
component.add(0, emailToName.get(component.get(0)));
}
return new ArrayList<>(ans.values());
}
class DSU {
int[] parent;
public DSU() {
parent = new int[10001];
for (int i = 0; i <= 10000; ++i)
parent[i] = i;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public int find2(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]]; // path compression by halving
x = parent[x];
}
return x;
}
public void union(int x, int y) {
parent[find(y)] = find(x);
}
}
public List<List<String>> accountsMergeWithDFS(List<List<String>> accounts) {
Map<String, String> emailToName = new HashMap<>();
Map<String, ArrayList<String>> graph = new HashMap<>();
for (List<String> account : accounts) {
String name = "";
for (String email : account) {
if (name == "") {
name = email;
continue;
}
graph.computeIfAbsent(email, x -> new ArrayList<String>()).add(account.get(1));
graph.computeIfAbsent(account.get(1), x -> new ArrayList<String>()).add(email);
emailToName.put(email, name);
}
}
Set<String> seen = new HashSet<>();
List<List<String>> ans = new ArrayList<>();
for (String email : graph.keySet()) {
if (!seen.contains(email)) {
seen.add(email);
Stack<String> stack = new Stack<>();
stack.push(email);
List<String> component = new ArrayList<>();
while (!stack.empty()) {
String node = stack.pop();
component.add(node);
for (String nei : graph.get(node)) {
if (!seen.contains(nei)) {
seen.add(nei);
stack.push(nei);
}
}
}
Collections.sort(component);
component.add(0, emailToName.get(email));
ans.add(component);
}
}
return ans;
}
Palindrome Questions
Longest Valid Parentheses
Given a string containing just the characters ‘(‘ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.
For “(()”, the longest valid parentheses substring is “()”, which has length = 2.
Another example is “)()())”, where the longest valid parentheses substring is “()()”, which has length = 4.
Solution:
Three ways: Dynamic Programming, Use Stack, Use 2 Counters
public class LongestValidParentheses {
/**
* We make use of two counters left and right, and traverse from left to right and right to
* left. Keep tracking the length of the current valid string.
*/
public static int longestValidParentheses(String s) {
int left = 0, right = 0, maxLen = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, 2 * right);
} else if (right > left) {
left = right = 0;
}
}
left = right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, 2 * left);
} else if (left > right) {
left = right = 0;
}
}
return maxLen;
}
/**
* We can make use of stack while scanning the given string to check if the string scanned so
* far is valid, and also the length of the longest valid string.
* push -1 in favor of easy coding, otherwise needs to check
* stock.isEmpty() before pop() and i - stack.peek() + 1
*/
public static int longestValidParentheses2(String s) {
int maxLen = 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(')
stack.push(i);
else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
maxLen = Math.max(maxLen, i - stack.peek());
}
}
}
return maxLen;
}
/**
* We make use of a dp array where ith element of dp represents the length of the longest valid
* substring ending at ith index.
*/
public static int longestValidParentheses3(String s) {
int maxLen = 0;
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
// s[i] = ')' and s[i-1] = '('
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else {
// s[i] = ')' and s[i-1] = ')'
int j = i - dp[i - 1]; // paired with s[i-1]
if (j > 0 && s.charAt(j - 1) == '(') { // paired with s[i]
dp[i] = dp[i - 1] + ((j >= 2 ? dp[j - 2] : 0)) + 2;
}
}
maxLen = Math.max(maxLen, dp[i]);
}
}
return maxLen;
}
}
Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example: Input: “babad”; Output: “bab”; Note: “aba” is also a valid answer.
Solution: Expand Around Center, Time Complexity O(N^2) where N is the length of S. Each expansion might do O(N) work.
public class LongestPalindromicSubstring {
private int start = 0;
private int maxLen = 0;
/**
* We observe that a palindrome mirrors around its center. Therefore, a palindrome can be
* expanded from its center, and there are only 2n - 1 such centers.
*/
public String longestPalindrome(String s) {
if (s == null || s.length() < 2)
return s;
for (int i = 0; i < s.length() - 1; i++) {
extendPalindrome(s, i, i); // between one, e.g. 'abcba'
extendPalindrome(s, i, i + 1); // between two, e.g. 'abccba'
}
return s.substring(start, start + maxLen);
}
private void extendPalindrome(String s, int lo, int hi) {
while (lo >= 0 && hi < s.length() && s.charAt(lo) == s.charAt(hi)) {
lo--;
hi++;
}
if (maxLen < hi - lo - 1) {
start = lo + 1;
maxLen = hi - lo - 1;
}
}
}
Palindrome Permutation
Given a string s, return all the palindromic permutations (without duplicates) of it. Return an empty list if no palindromic permutation could be form.
Example 1: Input: “aabb” Output: [“abba”, “baab”]
Solution: use Backtracking and time complexity is O((n/2+1)!).
public static List<String> generatePalindromes(String s) {
List<String> result = new ArrayList<>();
if (s == null || s.length() == 0)
return result;
int[] count = new int[128];
for (int i = 0; i < s.length(); i++)
count[s.charAt(i)]++;
int odd = -1;
for (int i = 0; i < count.length; i++) {
if (count[i] % 2 != 0) {
if (odd != -1) // found more than one odd!
return result;
odd = i; // cache this odd char
}
count[i] /= 2; // half it!
}
StringBuilder temp = new StringBuilder();
// just need to generate half length
generatePalindromesDfs(result, temp, count, s.length() / 2, odd);
return result;
}
private static void generatePalindromesDfs(List<String> result, StringBuilder builder, int[] count, int halfLen,
int oddChar) {
if (builder.length() == halfLen) {
// replicate another half!
if (oddChar != -1)
builder.append((char) oddChar);
for (int i = builder.length() - (oddChar == -1 ? 1 : 2); i >= 0; i--) {
builder.append(builder.charAt(i));
}
result.add(builder.toString());
return;
}
int prevLen = builder.length();
for (int i = 0; i < count.length; i++) {
if (count[i] > 0) {
builder.append((char) (i));
count[i]--;
generatePalindromesDfs(result, builder, count, halfLen, oddChar);
count[i]++;
builder.setLength(prevLen);
}
}
}
Super Palindromes
/**
* Let's say a positive integer is a super-palindrome if it is a palindrome, and it is also the
* square of a palindrome.
*
* Given two positive integers left and right represented as strings, return the number of
* super-palindromes integers in the inclusive range [left, right].
*
*
* <pre>
* Example 1:
* Input: left = "4", right = "1000"
* Output: 4
* Explanation: 4, 9, 121, and 484 are superpalindromes.
* Note that 676 is not a superpalindrome: 26 * 26 = 676, but 26 is not a palindrome.
* </pre>
*
* Solution: Say P = R^2 is a superpalindrome. R is a palindrome too. The first half of the digits
* in R determine R up to two possibilites. e.g. if k = 123, then R = 12321 or R = 123321.
*
*/
public class SuperPalindromes {
public int superpalindromesInRange(String sL, String sR) {
long left = Long.valueOf(sL);
long right = Long.valueOf(sR);
int max = 100000;
int ans = 0;
// count odd length;
for (int k = 1; k < max; k++) {
StringBuilder sb = new StringBuilder(Integer.toString(k));
for (int i = sb.length() - 2; i >= 0; i--)
sb.append(sb.charAt(i));
long v = Long.valueOf(sb.toString());
v *= v;
if (v > right)
break;
if (v >= left && isPalindrome(v))
ans++;
}
// count even length;
for (int k = 1; k < max; k++) {
StringBuilder sb = new StringBuilder(Integer.toString(k));
for (int i = sb.length() - 1; i >= 0; i--)
sb.append(sb.charAt(i));
long v = Long.valueOf(sb.toString());
v *= v;
if (v > right)
break;
if (v >= left && isPalindrome(v))
ans++;
}
return ans;
}
public boolean isPalindrome(long x) {
long m = x, n = 0;
while (m > 0) {
n = 10 * n + m % 10;
m /= 10;
}
return x == n;
}
}
Palindrome Pairs
Given a list of unique words, find all pairs of distinct indices (i, j) in the given list, so that the concatenation of the two words, i.e. words[i] + words[j] is a palindrome.
Example:
Input: ["abcd","dcba","lls","s","sssll"]
Output: [[0,1],[1,0],[3,2],[2,4]]
Explanation: The palindromes are ["dcbaabcd","abcddcba","slls","llssssll"]
The brute force solution is check each pair of words to see if they form a palindrome. The complexity is O(kn^2) where k is the length of the largest word in the input wordlist because we need to check isPalindrome() for each pair.
The solution is we can use build a Trie tree with each input word reverse, and has the index of each word as the end indicator.
Let’s suppose we’re trying to find all words that can match an input word A. We have two cases:
- The matching word is shorter than or the same size as A
- The matching word is longer than A
To find words in case 1, we can walk through our trie using the letters in A, every time we encounter a word ending, we can check the ‘rest’ of the letters in A to see if they form a palindrome.
To find words in case 2, we need to also check for palindromes below the node that the word we’re searching with ends on.
The complexity of this solution is O(k^2n) where k is the length of largest word. We are doing k^2 work put each work into the Trie (because we are doing isPalindrome checks that cost O(k) at each letter); also k^2 work to check and search Trie.
Also, we can leverage a hash map to implement the similar idea, please see solution #2.
Solution #1: Trie Tree
public List<List<Integer>> palindromePairs(String[] words) {
List<List<Integer>> res = new ArrayList<>();
// build trie with word reversed
TrieNode root = new TrieNode();
for (int i = 0; i < words.length; i++)
addWord(root, words[i], i);
for (int i = 0; i < words.length; i++)
search(words, i, root, res);
return res;
}
private void addWord(TrieNode root, String word, int index) {
for (int i = word.length() - 1; i >= 0; i--) {
int j = word.charAt(i) - 'a';
if (root.next[j] == null)
root.next[j] = new TrieNode();
// store all pandromes below current node
if (isPalindrome(word, 0, i))
root.list.add(index);
root = root.next[j];
}
root.list.add(index);
root.index = index;
}
private void search(String[] words, int i, TrieNode root, List<List<Integer>> res) {
for (int j = 0; j < words[i].length(); j++) {
if (root.index >= 0 && root.index != i && isPalindrome(words[i], j, words[i].length() - 1)) {
res.add(Arrays.asList(i, root.index));
}
root = root.next[words[i].charAt(j) - 'a'];
if (root == null)
return;
}
// the stored palindromes under this node
for (int j : root.list) {
if (i == j)
continue;
res.add(Arrays.asList(i, j));
}
}
private boolean isPalindrome(String word, int i, int j) {
while (i < j) {
if (word.charAt(i++) != word.charAt(j--))
return false;
}
return true;
}
class TrieNode {
TrieNode[] next;
int index;
List<Integer> list;
TrieNode() {
next = new TrieNode[26];
index = -1;
list = new ArrayList<>();
}
}
Solution #2: HashMap
// say this pair of words: {"dcbab","cd"}, we need check both "dcbabcd" and "cddcbab"
public List<List<Integer>> palindromePairs2(String[] words) {
List<List<Integer>> pairs = new LinkedList<>();
if (words == null || words.length == 0)
return pairs;
Map<String, Integer> map = new HashMap<>();
// add reversed words to map!
for (int i = 0; i < words.length; i++)
map.put(new StringBuilder(words[i]).reverse().toString(), i);
for (int i = 0; i < words.length; i++) {
String word = words[i];
int length = word.length();
// place the word on left side
int end = 0;
while (end < length) {
Integer j = map.get(word.substring(0, end));
if (j != null && i != j && isPalindrome(word.substring(end, length)))
pairs.add(Arrays.asList(i, j));
end++;
}
// place the word on right side
int begin = length - 1;
while (begin >= 0) {
Integer j = map.get(word.substring(begin, length));
if (j != null && i != j && isPalindrome(word.substring(0, begin)))
pairs.add(Arrays.asList(i, j));
begin--;
}
/*
int l = 0, r = 0;
while (l <= r) {
Integer j = map.get(word.substring(l, r));
// check both left and right side
if (j != null && i != j && isPalindrome(word.substring(l == 0 ? r : 0, l == 0 ? word.length() : l)))
pairs.add(l == 0 ? Arrays.asList(i, j) : Arrays.asList(j, i));
if (r < word.length())
r++;
else
l++;
}
*/
}
return pairs;
}
private boolean isPalindrome(String word) {
int i = 0, j = word.length() - 1;
while (i < j) {
if (word.charAt(i++) != word.charAt(j--))
return false;
}
return true;
}
Sliding Window Maximum
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
For example, Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.
Window position Max
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
Therefore, return the max sliding window as [3,3,5,5,6,7].
Solution:
We scan the array from 0 to n-1, keep the “promising” elements in the queue. The algorithm is amortized O(n) as each element is put and polled once.
public class SlidingWindowMaximum {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 0 || k <= 0)
return new int[0];
int[] result = new int[nums.length - k + 1];
Deque<Integer> queue = new LinkedList<>();
for (int i = 0; i < nums.length; i++) {
// discard if the element is out of the k size window
if (!queue.isEmpty() && queue.peek() < i - k + 1) {
queue.poll();
}
// discard elements smaller than nums[i] from the tail
while (!queue.isEmpty() && nums[queue.peekLast()] < nums[i]) {
queue.pollLast();
}
queue.offer(i);
if (i >= k - 1) {
result[i - k + 1] = nums[queue.peek()];
}
}
return result;
}
}
Sliding Window Median
The median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
For examples, if arr = [2,3,4], the median is 3; if arr = [1,2,3,4], the median is (2 + 3) / 2 = 2.5. You are given an integer array nums and an integer k.
There is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the median array for each window in the original array. Answers within 10-5 of the actual value will be accepted.
Example 1:
Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
Output: [1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000]
Explanation:
Window position Median
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
- Solution: Use two heaps with lazy removal
- Time complexity: \(O(2⋅n\log k)+O(n−k)≈O(n\log k)\).
- Space complexity: \(O(k)+O(n)≈O(n)\) extra linear space.
public class SlidingWindowMedian {
public double[] medianSlidingWindow(int[] nums, int k) {
Queue<Integer> large = new PriorityQueue<>((a, b) -> nums[a] == nums[b] ? Integer.compare(a, b) : Integer.compare(nums[a], nums[b]));
Queue<Integer> small = new PriorityQueue<>((a, b) -> nums[a] == nums[b] ? Integer.compare(a, b) : Integer.compare(nums[b], nums[a]));
double[] ans = new double[nums.length - k + 1];
int balance = 0;
int i = 0;
while (i < nums.length) {
if (large.isEmpty() || nums[i] >= nums[large.peek()]) {
large.offer(i);
balance++;
} else {
small.offer(i);
balance--;
}
i++;
while (balance > 1 || (!large.isEmpty() && large.peek() < i - k)) {
int min = large.poll();
if (min >= i - k) {
small.offer(min);
balance -= 2;
}
}
while (balance < 0 || (!small.isEmpty() && small.peek() < i - k)) {
int max = small.poll();
if (max >= i - k) {
large.offer(max);
balance += 2;
}
}
if (i - k >= 0) {
ans[i - k] = k % 2 == 0 ? ((double) nums[small.peek()] + (double) nums[large.peek()]) / 2 : (double) nums[large.peek()];
// Lazy removal of an outgoing number
if (!small.isEmpty() && i - k == small.peek()) {
small.poll();
balance++;
} else if (i - k == large.peek()) {
large.poll();
balance--;
} else if (nums[i - k] >= nums[large.peek()]) {
balance--;
} else {
balance++;
}
}
}
return ans;
}
}
Find Median from Data Stream
/**
* The median is the middle value in an ordered integer list. If the size of the list is even, there
* is no middle value and the median is the mean of the two middle values.
*
* For example, for arr = [2,3,4], the median is 3. For example, for arr = [2,3], the median is (2 +
* 3) / 2 = 2.5. Implement the MedianFinder class:
*
* MedianFinder() initializes the MedianFinder object. void addNum(int num) adds the integer num
* from the data stream to the data structure. double findMedian() returns the median of all
* elements so far. Answers within 10-5 of the actual answer will be accepted.
*
*/
public class MedianFinder {
private Queue<Integer> small;
private Queue<Integer> large;
public MedianFinder() {
large = new PriorityQueue<>();
small = new PriorityQueue<>(Collections.reverseOrder());
}
public void addNum(int num) {
if (large.size() > 0 && num > large.peek()) {
large.offer(num);
} else {
small.offer(num);
}
if (small.size() - large.size() == 2) {
large.offer(small.poll());
} else if (large.size() - small.size() == 2) {
small.offer(large.poll());
}
}
public double findMedian() {
if (small.size() > large.size()) {
return (double) small.peek();
} else if (large.size() > small.size()) {
return (double) large.peek();
} else {
return (small.peek() + large.peek()) / 2.0;
}
}
}
Expression Parser
Regular Expression Matching
Implement regular expression matching with support for . and *. . Matches any single character; * Matches zero or more of the preceding element. The matching should cover the entire input string (not partial).
Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true
isMatch("ab", ".*") → true
isMatch("aab", "c*a*b") → true
Solution:
-
The industry regular expression uses NFA and Graph search to implement. Nondeterministic finite-state automata (NFA) can “guess” the right one when faced with more than one way to try to match the pattern.
-
Regular expression are defined recursively, we can traverse down the string and check that the prefix of the string thus far matches the alphanumeric character or dot until some suffix is matched by the remainder of regular expression. Time and space complexity are both O((T+P)2^(T+P/2)).
-
Dynamic programming: we proceed with the same recursion as above, except because calls will only ever be made to match(text[i:], pattern[j:]), we use dp(i, j) to handle those calls instead, saving us expensive string-building operations and allowing us to cache the intermediate results. Time and space complexity are both O(TP).
-
To support
^and$: If the pattern’s first char is^, just remove it and check whether the rest pattern matches entire text; if the pattern’s last char is$, just check whether we reached the end of text right now!
// Top Down DP with Recursion
public static boolean regExpMatchTopDown(String text, String pattern) {
Boolean[][] memo = new Boolean[text.length() + 1][pattern.length() + 1];
return regExpMathRecursion(0, 0, text, pattern, memo);
}
private static boolean regExpMathRecursion(int i, int j, String text, String pattern, Boolean[][] memo) {
if (memo[i][j] != null)
return memo[i][j];
// base case, reached the end
if (j == pattern.length())
return i == text.length();
boolean firstMatch = i < text.length() && (pattern.charAt(j) == text.charAt(i) || pattern.charAt(j) == '.');
if (j + 1 < pattern.length() && pattern.charAt(j + 1) == '*') {
// skip 2 chars in pattern (just ignore x*) since * can much zero preceding elements.
// skip one char in text since * can match multiple times of this preceding elements!
memo[i][j] = regExpMathRecursion(i, j + 2, text, pattern, memo)
|| (firstMatch && regExpMathRecursion(i + 1, j, text, pattern, memo));
} else {
// skip a char for both pattern and text!
memo[i][j] = firstMatch && regExpMathRecursion(i + 1, j + 1, text, pattern, memo);
}
return memo[i][j];
}
// Bottom Up DP with Iteration
public static boolean regExpMatchBottomUp(String text, String pattern) {
boolean[][] dp = new boolean[text.length() + 1][pattern.length() + 1];
dp[text.length()][pattern.length()] = true;
for (int i = text.length(); i >= 0; i--) {
for (int j = pattern.length() - 1; j >= 0; j--) {
boolean firstMatch = i < text.length() && (pattern.charAt(j) == text.charAt(i) || pattern.charAt(j) == '.');
if (j + 1 < pattern.length() && pattern.charAt(j + 1) == '*') {
dp[i][j] = dp[i][j + 2] || (firstMatch && dp[i + 1][j]);
} else {
dp[i][j] = firstMatch && dp[i + 1][j + 1];
}
}
}
return dp[0][0];
}
Expression Add Operators
Given a string that contains only digits 0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value.
Examples:
"123", 6 -> ["1+2+3", "1*2*3"]
"232", 8 -> ["2*3+2", "2+3*2"]
"105", 5 -> ["1*0+5","10-5"]
"00", 0 -> ["0+0", "0-0", "0*0"]
"3456237490", 9191 -> []
Solution:
This problem has a lot of edge cases to be considered:
- Overflow: we use a long type once it is larger than Integer.MAX_VALUE or minimum, we get over it.
- 0 sequence: because we can’t have numbers with multiple digits started with zero, we have to deal with it too.
- A little trick is that we should save the value that is to be multiplied in the next recursion.
For each pair of characters, we can choose to insert a +, -, * or no operator. If the length of A is n, the number of such operations is n - 1, implying we can have 4^(n-1) combinations. The time complexity is O(n4^n), since each expression takes time O(n) to evaluate.
public List<String> addOperators(String num, int target) {
List<String> result = new ArrayList<>();
if (num == null || num.length() == 0)
return result;
helper(result, "", num, target, 0, 0, 0);
return result;
}
private void helper(List<String> result, String path, String num, int target, int pos, long eval, long multied) {
if (pos == num.length()) {
if (target == eval)
result.add(path);
return;
}
for (int i = pos; i < num.length(); i++) {
// when starts with 0, only one digit is valid!
if (num.charAt(pos) == '0' && i != pos)
break;
long cur = Long.parseLong(num.substring(pos, i + 1));
if (pos == 0) {
helper(result, path + cur, num, target, i + 1, cur, cur);
} else {
helper(result, path + "+" + cur, num, target, i + 1, eval + cur, cur);
helper(result, path + "-" + cur, num, target, i + 1, eval - cur, -cur);
helper(result, path + "*" + cur, num, target, i + 1, eval - multied + multied * cur, multied * cur);
}
}
}
Next Closest Time
Given a time represented in the format “HH:MM”, form the next closest time by reusing the current digits. There is no limit on how many times a digit can be reused.
You may assume the given input string is always valid. For example, “01:34”, “12:09” are all valid. “1:34”, “12:9” are all invalid.
Example 1:
Input: "19:34"
Output: "19:39"
Explanation: The next closest time choosing from digits 1, 9, 3, 4, is 19:39, which occurs 5 minutes later. It is not 19:33, because this occurs 23 hours and 59 minutes later.
public String nextClosestTime(String time) {
int start = 60 * Integer.parseInt(time.substring(0, 2));
start += Integer.parseInt(time.substring(3));
int ans = start;
int elapsed = 24 * 60;
Set<Integer> allowed = new HashSet<>();
for (char c : time.toCharArray())
if (c != ':') {
allowed.add(c - '0');
}
for (int h1 : allowed) {
for (int h2 : allowed) {
if (h1 * 10 + h2 < 24) {
for (int m1 : allowed) {
for (int m2 : allowed) {
if (m1 * 10 + m2 < 60) {
int cur = 60 * (h1 * 10 + h2) + (m1 * 10 + m2);
int candElapsed = Math.floorMod(cur - start, 24 * 60);
if (0 < candElapsed && candElapsed < elapsed) {
ans = cur;
elapsed = candElapsed;
}
}
}
}
}
}
}
return String.format("%02d:%02d", ans / 60, ans % 60);
}
Implement Huffman Coding
Given a set of characters with corresponding frequencies, find a code book that has the smallest average code length.
Solution:
Huffman coding proceeds in three steps:
- Sort characters in increasing order of frequencies and create a binary tree node for each character, call this set by
S. - Create a new node u whose children are the two nodes with smallest frequencies and whose frequency is the sum of children’s frequencies.
- Remove the children from
Sand addutoS. Repeat from Step 2 tillSconsists of a single node, which is the root. - Mark all the left edges with 0 and the right edges with 1. The path from the root to a leaf node yields the bit string encoding the corresponding character.
It requires two extract-min and one insert operation, it takes O(nlogn) time to build the Huffman tree. It’s possible for the tree to be very skewed. In such a situation, the codewords are of length 1, 2, 3,…, n, so the time to generate the codebook becomes O(1+2+..+n)=O(n^2).
public class HuffmanEncoding {
static class Symbol {
char chr;
double freq;
String code;
public Symbol(char chr, double freq) {
this.chr = chr;
this.freq = freq;
}
}
static class TreeNode {
double freqSum;
Symbol symbol;
TreeNode left, right;
public TreeNode(double freqSum, Symbol symbol, TreeNode left, TreeNode right) {
this.freqSum = freqSum;
this.symbol = symbol;
this.left = left;
this.right = right;
}
}
public static Map<Character, String> huffmanEncoding(List<Symbol> symbols) {
Queue<TreeNode> candidates = new PriorityQueue<>((a, b) -> (Double.compare(a.freqSum, b.freqSum)));
// add symbols as leaves
for (Symbol symbol : symbols) {
candidates.add(new TreeNode(symbol.freq, symbol, null, null));
}
// keep combining two nodes utils there is one node left, which is the root.
while (candidates.size() > 1) {
TreeNode left = candidates.remove();
TreeNode right = candidates.remove();
candidates.add(new TreeNode(left.freqSum + right.freqSum, null, left, right));
}
Map<Character, String> huffmanEncoding = new HashMap<>();
assignHuffmanCode(candidates.peek(), new StringBuilder(), huffmanEncoding);
return huffmanEncoding;
}
public static void assignHuffmanCode(TreeNode tree, StringBuilder code, Map<Character, String> huffmanEncoding) {
if (tree != null) {
if (tree.symbol != null) {
// this node is a leaf
huffmanEncoding.put(tree.symbol.chr, code.toString());
tree.symbol.code = code.toString();
} else {
assignHuffmanCode(tree.left, code.append('0'), huffmanEncoding);
code.setLength(code.length() - 1); // backtrack
assignHuffmanCode(tree.right, code.append('1'), huffmanEncoding);
code.setLength(code.length() - 1); // backtrack
}
}
}
public static void main(String[] args) {
double[] ENGLISH_FREQ = { 8.167, 1.492, 2.782, 4.253, 12.702, 2.228, 2.015, 6.094, 6.966, 0.153, 0.772, 4.025,
2.406, 6.749, 7.507, 1.929, 0.095, 5.987, 6.327, 9.056, 2.758, 0.978, 2.360, 0.150, 1.974, 0.074 };
List<Symbol> symbols = new ArrayList<>();
for (int i = 0; i < 26; ++i) {
symbols.add(new Symbol((char) ('a' + i), ENGLISH_FREQ[i]));
}
Map<Character, String> result = huffmanEncoding(symbols);
double avg = 0.0;
for (Symbol symbol : symbols) {
System.out.println(symbol.chr + "\t" + symbol.freq + "\t" + result.get(symbol.chr));
avg += symbol.freq / 100 * result.get(symbol.chr).length();
}
System.out.println("Average huffman code length = " + avg);
assert avg > 4.2 && avg < 4.3;
}
}
Best New Highway Section
Write a program which takes the existing highway network, and proposals for new highway sections, and returns the proposed highway section which leads to the most improvement in the total driving distance.
Solution:
We can improve upon this by running the all pairs shortest paths algorithm just once. Let S(u,v) be the 2D array of shortest path distances for each pair of cities. Each proposal p is a pair of cities (x,y). For the pair of cities (a,b), the best we can do by using proposal p is min(S(a,b),S(a,x)+d(x,y)+S(y,b),S(a,y)+d(y,x)+S(x,b)). This results in a \(O(n^3 + kn^2)\) time complexity.
public class RoadNetwork {
static class Section {
int x, y;
double distance;
public Section(int x, int y, double distance) {
this.x = x;
this.y = y;
this.distance = distance;
}
@Override
public String toString() {
return x + "->" + y + ": " + distance;
}
}
public static Section findBestProposals(Section[] H, Section[] P, int n) {
// graph stores the shortest path distances between all pairs of vertices.
double[][] graph = new double[n][n];
// prepare the graph in favor of Floyd Warshall algorithm
for (int i = 0; i < n; i++) {
Arrays.fill(graph[i], Double.MAX_VALUE);
}
for (int i = 0; i < n; i++) {
graph[i][i] = 0.0; // self
}
// build an undirected graph based on existing sections
for (Section h : H) {
graph[h.x][h.y] = h.distance;
graph[h.y][h.x] = h.distance;
}
// perform Floyd-Warshall algorithm: O(n^3)
for (int k = 0; k < graph.length; k++) {
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph.length; j++) {
if (graph[i][k] != Double.MAX_VALUE && graph[k][j] != Double.MAX_VALUE) {
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}
}
}
}
// examines each proposal for shorter distance for all pairs.
double bestDistanceSaving = Double.MIN_VALUE;
Section bestProposal = new Section(-1, -1, 0.0);
for (Section p : P) {
double proposalSaving = 0.0;
for (int a = 0; a < n; a++) {
for (int b = 0; b < n; b++) {
double saving = graph[a][b] - (graph[a][p.x] + p.distance + graph[p.y][b]);
proposalSaving += saving > 0.0 ? saving : 0.0;
}
}
if (proposalSaving > bestDistanceSaving) {
bestDistanceSaving = proposalSaving;
bestProposal = p;
}
}
return bestProposal;
}
public static void main(String[] args) {
Section[] H = new Section[] { new Section(0, 1, 10), new Section(1, 2, 10), new Section(2, 3, 10) };
Section[] P = new Section[] { new Section(0, 3, 1), new Section(0, 2, 2), new Section(0, 1, 3) };
Section best = findBestProposals(H, P, 4);
assert (best.x == 0 && best.y == 3 && best.distance == 1.0);
}
}
Test If Arbitrage Exists
Suppose you are given a set of exchange rates among currencies, design an efficient algorithm to determine whether there exists an arbitrage, a way to start with a single unit of some currency C and convert it back to more than one unit of C through a sequence of exchanges.
 |
 |
Solution:
An arbitrage opportunity is a directed cycle such that the product of the exchange rates is greater than one. For example, our table says that 1,000 U.S. dollars will buy 1,000.00 × .741 = 741 euros, then we can buy 741 × 1.366 = 1,012.206 Canadian dollars with our euros, and finally, 1,012.206 × .995 = 1,007.14497 U.S. dollars with our Canadian dollars, a 7.14497-dollar profit!
To formulate the arbitrage problem as a negative-cycle detection problem, replace each weight by its logarithm, negated. With this change, computing path weights by multiplying edge weights in the original problem corresponds to adding them in the transformed problem.
-ln(.741) = 0.2998, -ln(1.366) = -0.3119
Rate(a->b) * Rate(b->c) * Rate(c->d) * ... * Rate(n->a) > 1
However, we need to convert the above inequality into a summation because standard graph algorithms add the edge weights during traversal. Hence, we take the logarithm of the above:
log(Rate(a->b)) + log(Rate(b->c)) + log(Rate(c->d)) + ... + log(Rate(n->a)) > log(1) == 0
Multiply the above by -1, the current arbitrage problem reduces to finding a negative cycle in the graph. Such a cycle can be solved using the Bellman-Ford algorithm.
-log(Rate(a->b)) - log(Rate(b->c)) - log(Rate(c->d)) - ... - log(Rate(n->a)) < 0
public static boolean isArbitrageExist(double[][] graph) {
// transforms each edge's weight
for (double[] edges : graph) {
for (int i = 0; i < edges.length; i++) {
edges[i] = -Math.log10(edges[i]);
}
}
// use Bellman-Ford algorithm to find negative weight cycle
double[] distances = new double[graph.length];
Arrays.fill(distances, Double.MAX_VALUE);
distances[0] = 0.0;
// repeat on all edges until no more cost updates occur.
for (int times = 1; times < graph.length; times++) {
boolean haveUpdated = false;
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph.length; j++) {
if (distances[i] != Double.MAX_VALUE && distances[j] > distances[i] + graph[i][j]) {
haveUpdated = true;
distances[j] = distances[i] + graph[i][j];
}
}
}
// no update in this iteration means no negative cycle
if (!haveUpdated) {
return false;
}
}
// detects cycle if there is any further update
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph.length; j++) {
if (distances[i] != Double.MAX_VALUE && distances[i] > distances[i] + graph[i][j]) {
return true;
}
}
}
return false;
}
Measure With Defective Jugs
You have three defective measuring jugs: A, B and C. They can only measure a range [230, 240]mL, [290,310]mL and [500, 515]mL. Please calculate if there exists a sequence of steps by which the required range [2100, 2300]mL of milk can be obtained.
NOTE: It’s not possible to pour one jug’s milk into another.
Solution:
It is natural to solve this problem using recursion. We can implement a general purpose function which finds the feasibility among n jugs. Also we cache intermediate computations to reduce number of recursive calls. The time complexity is O((L+1)(H+1)n), there are at most (L+1)(H+1) calls to check feasible for each recursion.
public class MeasureWithDefectiveJugs {
class Range {
int low, high;
public Range(int low, int high) {
this.low = low;
this.high = high;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null || !(obj instanceof Range))
return false;
Range range = (Range) obj;
return low == range.low && high == range.high;
}
@Override
public int hashCode() {
return Objects.hash(low, high);
}
}
class Jug extends Range {
public Jug(int low, int high) {
super(low, high);
}
}
public boolean checkFeasible(List<Jug> jugs, int L, int H) {
Set<Range> cache = new HashSet<>();
return checkFeasible(jugs, L, H, cache);
}
private boolean checkFeasible(List<Jug> jugs, int L, int H, Set<Range> cache) {
if (L > H || cache.contains(new Range(L, H)) || (L < 0 && H < 0))
return false;
// check each jug to see if it is possible
for (Jug jug : jugs) {
// base case: jug is in [L, H]
if ((L < jug.low && jug.high < H))
return true;
if (checkFeasible(jugs, L - jug.low, H - jug.high, cache))
return true;
}
// marks this range as impossible
cache.add(new Range(L, H));
return false;
}
public static void main(String[] args) {
MeasureWithDefectiveJugs solution = new MeasureWithDefectiveJugs();
List<Jug> jugs = new ArrayList<>();
jugs.add(solution.new Jug(230, 240));
jugs.add(solution.new Jug(290, 310));
jugs.add(solution.new Jug(500, 515));
assert solution.checkFeasible(jugs, 2100, 2300);
assert solution.checkFeasible(jugs, 2100, 2150) == false;
}
}