Arrays and Strings
- The array questions and string questions are often interchangeable.
- The time complexity to delete or insert an element at index i without resizing is O(n - i).
- Instead of deleting/inserting an entry (which requires shifting entries), consider overwriting it.
- When operating on 2D arrays, use parallel logic for rows and for columns.
- String objects are immutable, a[i] is likely to be faster than s.charAt(i) in typical Java implementation.
- The use of character-indexed arrays (e.g. Alphabet) only need an array with one entry for each alphabet character, instead of always use an array of length 65,536.
public Alphabet(String alpha) {
// check that alphabet contains no duplicate chars
boolean[] unicode = new boolean[Character.MAX_VALUE];
for (int i = 0; i < alpha.length(); i++) {
char c = alpha.charAt(i);
if (unicode[c])
throw new IllegalArgumentException("Illegal alphabet: repeated character = '" + c + "'");
unicode[c] = true;
}
alphabet = alpha.toCharArray();
R = alpha.length();
inverse = new int[Character.MAX_VALUE];
for (int i = 0; i < inverse.length; i++)
inverse[i] = -1;
// can't use char since R can be as big as 65,536
for (int c = 0; c < R; c++)
inverse[alphabet[c]] = c;
}
public int toIndex(char c) {
if (c >= inverse.length || inverse[c] == -1) {
throw new IllegalArgumentException("Character " + c + " not in alphabet");
}
return inverse[c];
}
public char toChar(int index) {
if (index < 0 || index >= R) {
throw new IllegalArgumentException("index must be between 0 and " + R + ": " + index);
}
return alphabet[index];
}
// %java Count 0123456789 < pi.txt
public static void main(String[] args) {
Alphabet alphabet = new Alphabet(args[0]);
final int R = alphabet.radix();
int[] count = new int[R]; // just need an array of R (for each character)
while (StdIn.hasNextChar()) {
char c = StdIn.readChar();
if (alphabet.contains(c))
count[alphabet.toIndex(c)]++;
}
for (int c = 0; c < R; c++)
StdOut.println(alphabet.toChar(c) + " " + count[c]);
}
Arrays Boot Camp
Rotate Array
Write an function, left rotate an array of size n by d.
Rotate one item a time, rotate total d times!
public void leftRotate(int[] nums, int d, int n) {
for (int i = 0; i < d; i++) {
int j = 0, temp = nums[0];
for (j = 0; j < n - 1; j++) {
nums[j] = nums[j + 1];
}
nums[j] = temp;
}
}
Write an function, right rotate an array of size n by d.
Use a few times of array-reverse function.
public void rightRotate(int[] nums, int d) {
d %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, d - 1);
reverse(nums, d, nums.length - 1);
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
swap(nums, start++, end--);
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
Move Zeros
Given an array nums, write a function to move all 0’s to the end of it while maintaining the relative order of the non-zero elements.
Example: Input: [0,1,0,3,12], Output: [1,3,12,0,0]
public void moveZeroes(int[] nums) {
for (int insertNonZeroAt = 0, i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
// reduce extra swap
if (i != insertNonZeroAt) {
int temp = nums[i];
nums[i] = nums[insertNonZeroAt];
nums[insertNonZeroAt] = temp;
}
insertNonZeroAt++;
}
}
}
Wiggle Sort
Given an unsorted array nums, reorder it in-place such that nums[0] <= nums[1] >= nums[2] <= nums[3]…. For example, given nums = [3, 5, 2, 1, 6, 4], one possible answer is [3, 5, 1, 6, 2, 4].
public void wiggleSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
if ((i % 2 == 0 && nums[i - 1] < nums[i]) || (i % 2 != 0 && nums[i - 1] > nums[i])) {
int tmp = nums[i];
nums[i] = nums[i - 1];
nums[i - 1] = tmp;
}
}
}
Even/Odd Sort
Reorder an array of integers so that even entries appear first. Solve it without allocating additional storage.
We need 2 pointers, one for even and another for odd number. We can sweep from left to right or both ends.
public void evenOddSort(int[] nums) {
int even = 0, odd = nums.length - 1;
while (even < odd) {
if (nums[even] % 2 == 0) {
even++;
} else {
// only swap for even num!
if (nums[odd] % 2 == 0) {
int temp = nums[even];
nums[even] = nums[odd];
nums[odd] = temp;
}
odd--;
}
}
}
Can Place Flowers
Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die.
Given a flowerbed (represented as an array containing 0 and 1, where 0 means empty and 1 means not empty), and a number n, return if n new flowers can be planted in it without violating the no-adjacent-flowers rule.
Example: Input: flowerbed = [1,0,0,0,1], n = 1 Output: True Example: Input: flowerbed = [1,0,0,0,1], n = 2 Output: False
_
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int i = 0, count = 0;
while (i < flowerbed.length) {
if (flowerbed[i] == 0 && (i == 0 || flowerbed[i - 1] == 0)
&& (i == flowerbed.length - 1 || flowerbed[i + 1] == 0)) {
flowerbed[i++] = 1;
count++;
}
if (count >= n) // stop as soon as count becomes equal to n
return true;
i++;
}
return false;
}
Sorted Squares Array
Given a sorted array of integers, return the sorted squares of those integers Ex: [-2,-4,1,3,5] -> [1,4,9,16,25]
public static int[] squareSort(int[] array) {
if (array == null || array.length == 0)
return new int[0];
int[] result = new int[array.length];
int i = 0, j = 0;
// while (i < array.length && array[i] < 0)
// i++;
i = binarySearch(array, 0);
j = i - 1;
int index = 0;
while (j >= 0 || i < array.length) {
if (j < 0) {
result[index++] = array[i] * array[i];
i++;
} else if (i >= array.length) {
result[index++] = array[j] * array[j];
j--;
} else if (Math.abs(array[j]) > array[i]) {
result[index++] = array[i] * array[i];
i++;
} else {
result[index++] = array[j] * array[j];
j--;
}
}
return result;
}
private static int binarySearch(int[] array, int target) {
int left = 0, right = array.length - 1;
// find the value >= target
while (left <= right) {
int mid = left + (right - left) / 2;
if (target == array[mid])
return mid;
else if (target < array[mid])
right = mid - 1;
else
left = mid + 1;
}
return left;
}
public static void main(String[] args) {
assert Arrays.equals(squareSort(new int[] { -4, 1, 3, 5 }), new int[] { 1, 9, 16, 25 });
assert Arrays.equals(squareSort(new int[] { 0, 1, 3, 5 }), new int[] { 0, 1, 9, 25 });
assert Arrays.equals(squareSort(new int[] { -5, -4, -1 }), new int[] { 1, 16, 25 });
assert Arrays.equals(squareSort(new int[] { -4, -1, 0, 3, 5, 5 }), new int[] { 0, 1, 9, 16, 25, 25 });
}
Advance Through Array
Write a program which takes an array of n integers, where A[i] denotes the maximum you can advance from index i, and returns whether it is possible to advance to the last index starting from the beginning of the array.
public boolean canReachEnd(int[] maxAdvancedSteps) {
int furthestReachSoFar = 0, lastIndex = maxAdvancedSteps.length - 1;
for (int i = 0; i <= furthestReachSoFar && furthestReachSoFar < lastIndex; i++) {
furthestReachSoFar = Math.max(furthestReachSoFar, maxAdvancedSteps[i] + i);
}
return furthestReachSoFar >= lastIndex;
}
Generate Pascal Triangle
Given numRows, generate the first numRows of Pascal’s triangle.
For example, given numRows = 5, Return
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
public List<List<Integer>> generatePascalTriangle(int numRows) {
List<List<Integer>> result = new ArrayList<>();
for (int i = 0; i < numRows; i++) {
List<Integer> currRow = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (0 < j && j < i)
currRow.add(result.get(i - 1).get(j - 1) + result.get(i - 1).get(j));
else
currRow.add(1);
}
result.add(currRow);
}
return result;
}
Two Sum Equals
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
Given nums = [2, 7, 11, 15], target = 9, Because nums[0] + nums[1] = 2 + 7 = 9, return [0, 1].
public int[] twoSum(int[] numbers, int target) {
int[] result = new int[2];
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < numbers.length; i++) {
if (map.containsKey(target - numbers[i])) {
result[1] = i;
result[0] = map.get(target - numbers[i]);
return result;
}
map.put(numbers[i], i);
}
return result;
}
If given an array of integers that is already sorted in ascending order, we should use 2 pointers.
public int[] twoSum2(int[] numbers, int target) {
int i = 0, j = numbers.length - 1;
while (i < j) {
int sum = numbers[i] + numbers[j];
if (sum == target)
return new int[] { i + 1, j + 1 };
else if (sum < target)
i++;
else
j--;
}
return new int[] { -1, -1 };
}
If needs design and implement a TwoSum class which support add and find.
public class TwoSum {
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
// Add the number to an internal data structure.
public void add(int number) {
if (map.containsKey(number)) {
map.put(number, map.get(number) + 1);
} else {
map.put(number, 1);
}
}
// Find if there exists any pair of numbers which sum is equal to the value.
public boolean find(int value) {
Iterator<Integer> iter = map.keySet().iterator();
while (iter.hasNext()) {
int num1 = iter.next();
int num2 = value - num1;
if (map.containsKey(num2)) {
if (num1 != num2 || map.get(num2) >= 2) {
return true;
}
}
}
return false;
}
}
Three Sum Equals
Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note: The solution set must not contain duplicate triplets.
For example, given array S = [-1, 0, 1, 2, -1, -4],
A solution set is: [ [-1, 0, 1], [-1, -1, 2] ]
The following solution has O(1) space complexity, and the time complexity is the sum of the time taken to sort O(nlog(n)), and then run the O(n) algorithm to find a pair in a sorted array that sums to specified value, which is O(n^2) overall.
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> list = new LinkedList<>();
for (int i = 0; i < nums.length - 2; i++) {
if (i > 0 && nums[i] == nums[i - 1]) // skip duplicates
continue;
int lo = i + 1, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[i] + nums[lo] + nums[hi];
if (sum == 0) {
list.add(Arrays.asList(nums[i], nums[lo], nums[hi]));
while (lo < hi && nums[lo] == nums[lo + 1]) // skip duplicates
lo++;
while (lo < hi && nums[hi] == nums[hi - 1]) // skip duplicates
hi--;
lo++;
hi--;
} else if (sum < 0)
lo++;
else
hi--;
}
}
return list;
}
Count of Range Sum
Given an integer array nums and two integers lower and upper, return the number of range sums that lie in [lower, upper] inclusive.
Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j inclusive, where i <= j.
Example 1:
Input: nums = [-2,5,-1], lower = -2, upper = 2 Output: 3 Explanation: The three ranges are: [0,0], [2,2], and [0,2] and their respective sums are: -2, -1, 2.
// Divide and conquer O(nlog(n))
public int countRangeSum(int[] nums, int lower, int upper) {
// easy to cover edge cases with one extra space
long[] sums = new long[nums.length + 1];
// calculate prefix sums
for (int i = 1; i < sums.length; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
return divide(sums, new long[sums.length], 0, sums.length - 1, lower, upper);
}
public int divide(long[] sums, long[] temp, int low, int high, int lower, int upper) {
if (low >= high)
return 0;
int count = 0, mid = (low + high + 1) / 2;
count += divide(sums, temp, low, mid - 1, lower, upper);
count += divide(sums, temp, mid, high, lower, upper);
count += merge(sums, temp, low, mid, high, lower, upper);
return count;
}
public int merge(long[] sums, long[] temp, int low, int mid, int high, int lower, int upper) {
// low~mid and mid+1~high are both sorted at this point
// Scan the left half and pair with right half
int count = 0, start = mid, end = mid;
for (int i = low; i < mid; i++) {
while (start <= high && sums[start] - sums[i] < lower)
start++;
while (end <= high && sums[end] - sums[i] <= upper)
end++;
count += end - start;
}
// mid belongs to the right half
int current = low, left = low, right = mid;
while (left < mid && right <= high) {
if (sums[left] <= sums[right]) {
temp[current++] = sums[left++];
} else {
temp[current++] = sums[right++];
}
}
// copy the rest of left half
while (left < mid) {
temp[current++] = sums[left++];
}
// copy the rest of right half
while (right <= high) {
temp[current++] = sums[right++];
}
// copy sorted temp (low~high) to sums
System.arraycopy(temp, low, sums, low, high - low + 1);
return count;
}
Compute Moving Average
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window. For example,
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3
The tricky is the current insert position stores previous value (-window size) and just need to be set to new value!
public class MovingAverage {
private int[] window;
private int count = 0, insert = 0;
private long sum = 0;
public MovingAverage(int size) {
if (size <= 0)
throw new IllegalArgumentException();
window = new int[size];
}
public double next(int value) {
if (count < window.length)
count++;
sum -= window[insert];
sum += value;
window[insert] = value;
insert = (insert + 1) % window.length;
return (double) sum / count;
}
}
K Empty Slots
There is a garden with N slots. In each slot, there is a flower. The N flowers will bloom one by one in N days. In each day, there will be exactly one flower blooming and it will be in the status of blooming since then.
Given an array flowers consists of number from 1 to N. Each number in the array represents the place where the flower will open in that day.
For example, flowers[i] = x means that the unique flower that blooms at day i will be at position x, where i and x will be in the range from 1 to N.
Also given an integer k, you need to output in which day there exists two flowers in the status of blooming, and also the number of flowers between them is k and these flowers are not blooming.
If there isn’t such day, output -1.
Example 1:
Input:
flowers: [1,3,2]
k: 1
Output: 2
Explanation: In the second day, the first and the third flower have become blooming.
Example 2:
Input:
flowers: [1,2,3]
k: 1
Output: -1
Solution: Use fixed-size sliding window. The idea is to use days[] to record each position’s flower’s blooming day. That means days[i] is the blooming day of the flower in position i+1. We just need to find a subarray days[left, left+1,…, left+k-1, right] which satisfies: for any i = left+1,…, left+k-1, we can have days[left] < days[i] && days[right] < days[i]. Then, the result is max(days[left], days[right])
public int kEmptySlots(int[] flowers, int k) {
int[] days = new int[flowers.length];
for (int i = 0; i < flowers.length; i++)
days[flowers[i] - 1] = i + 1;
int left = 0, right = k + 1, minDay = Integer.MAX_VALUE;
for (int i = 0; right < days.length; i++) {
if (days[i] < days[left] || days[i] <= days[right]) {
if (i == right)
minDay = Math.min(minDay, Math.max(days[left], days[right])); // we get a valid subarray
left = i;
right = k + 1 + i;
}
}
return (minDay == Integer.MAX_VALUE) ? -1 : minDay;
}
Shuffle An Array
Also can continuously maintaining a uniform random subset of size k of the sequence, called streamShuffle()!
public class ShuffleAnArray {
private Random random;
private int[] array;
private int[] original;
private int[] runningSample;
private int numSeenSoFar;
public ShuffleAnArray(int[] nums, int sampleSize) {
this.random = new Random();
this.array = nums;
this.original = nums.clone();
this.runningSample = new int[sampleSize];
}
public int[] reset() {
array = original;
original = original.clone();
numSeenSoFar = 0;
Arrays.fill(runningSample, 0);
return array;
}
public int[] shuffle() {
for (int i = 0; i < array.length; i++) {
swapAt(i, i + random.nextInt(array.length - i));
}
return array;
}
public int[] shuffle(int k) {
for (int i = 0; i < k; i++) {
swapAt(i, i + random.nextInt(array.length - i));
}
return Arrays.copyOfRange(array, 0, k);
}
public int[] streamShuffle(Iterator<Integer> sequence) {
while (sequence.hasNext()) {
int x = sequence.next();
numSeenSoFar++;
// fill up the running sample first
if (numSeenSoFar < runningSample.length) {
runningSample[numSeenSoFar - 1] = x;
} else {
int i = random.nextInt(numSeenSoFar);
if (i < runningSample.length)
runningSample[i] = x;
}
}
return runningSample;
}
private void swapAt(int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
Top K Frequent Elements
Given a non-empty array of integers, return the k most frequent elements.
- Example 1: Input: nums = [1,1,1,2,2,3], k = 2 Output: [1,2]
- Example 2: Input: nums = [1], k = 1 Output: [1]
Solution: Use Bucket Sort O(n).
public List<Integer> topKFrequent(int[] nums, int k) {
List<Integer> result = new ArrayList<>();
if (nums.length == 0)
return result;
// Avoid using hash map
int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
if (nums[i] < min)
min = nums[i];
if (nums[i] > max)
max = nums[i];
}
int[] data = new int[max - min + 1];
for (int i = 0; i < nums.length; i++) {
data[nums[i] - min]++;
}
// Index is frequency
@SuppressWarnings("unchecked")
List<Integer>[] bucket = new ArrayList[nums.length + 1];
for (int i = 0; i < data.length; i++) {
if (data[i] > 0) {
if (bucket[data[i]] == null) {
bucket[data[i]] = new ArrayList<Integer>();
}
bucket[data[i]].add(i + min);
}
}
for (int i = nums.length; i >= 0 && result.size() < k; i--) {
if (bucket[i] != null)
result.addAll(bucket[i]);
}
return result;
}
Random Permutation
To create uniformly random permutations of {0, 1, …, n - 1}, we can apply above Shuffle An Array solution, at each iteration the array is partitioned into the partial permutation and remaining values.
A Random Subset
Write a program that takes as input a positive integer n and a size k <= n, and return a size k random subset of {0, 1, 2, …, n - 1}. Here the order doesn’t matter.
We are going to use a hash table to track entries of the array which have been touched in the process of randomization. These are entries A[i] which may not equal i, the hash table is updated as the algorithm advances.
For example, suppose n = 100 and k = 4. In the first iteration, suppose we get the random number 28. We update H to (0,28),(28,0). This means that A[0] is 28 and A[28] is 0 – for all other i, A[i] = i. In the second iteration, suppose we get the random number 42. We update H to (0,28),(28,0),(1,42),(42,1). In the third iteration, suppose we get the random number 28 again. We update H to (0,28),(28,2),(1,42),(42,1),(2,0). In the fourth iteration, suppose we get the random number 64. We update H to (0,28),(28,2),(1,42),(42,1),(2,0),(3,64),(64,3). The random subset is the 4 elements corresponding to indices 0,1,2,3, i.e., [28, 42, 0, 64].
public List<Integer> randomSubset(int n, int k) {
Map<Integer, Integer> changedElements = new HashMap<>();
Random randIdxGen = new Random();
for (int i = 0; i < k; i++) {
int randIdx = i + randIdxGen.nextInt(n - i);
Integer ptr1 = changedElements.get(randIdx);
Integer ptr2 = changedElements.get(i);
if (ptr1 == null && ptr2 == null) {
changedElements.put(randIdx, i);
changedElements.put(i, randIdx);
} else if (ptr1 == null && ptr2 != null) {
changedElements.put(randIdx, ptr2);
changedElements.put(i, randIdx);
} else if (ptr1 != null && ptr2 == null) {
changedElements.put(i, ptr1);
changedElements.put(randIdx, i);
} else {
changedElements.put(i, ptr1);
changedElements.put(randIdx, ptr2);
}
}
List<Integer> result = new ArrayList<>(k);
for (int i = 0; i < k; i++) {
result.add(changedElements.get(i));
}
return result;
}
Nonuniform Random Number
Given n numbers as well as probabilities p0, p1, …, p(n-1), which sum up to 1. How would you generate one of the n numbers according to the specified probabilities?
We can solve the problem by partitioning the unit interval [0, 1] into n disjoint segments, in a way so that the length of the jth interval is proportional to p(j).
public int nonuniformRandomNumber(List<Integer> values, List<Double> probabilities) {
List<Double> prefixSumOfProbabilities = new ArrayList<>();
prefixSumOfProbabilities.add(0.0);
for (double p : probabilities) {
prefixSumOfProbabilities.add(prefixSumOfProbabilities.get(prefixSumOfProbabilities.size() - 1) + p);
}
Random r = new Random();
// Get a random number in [0.0,1.0).
final double uniform01 = r.nextDouble();
// Find the index of the interval that uniform01 lies in.
int it = Collections.binarySearch(prefixSumOfProbabilities, uniform01);
if (it < 0) {
// We want the index of the first element in the array which is greater than the key.
//
// When a key is not present in the array, Collections.binarySearch() returns the
// negative of (1 plus the smallest index) whose entry is greater than the key.
//
// Therefore, if the return value is negative, by taking its absolute value minus 1 and
// substracting 1 from it, we get the desired index.
final int intervalIdx = (Math.abs(it) - 1) - 1;
return values.get(intervalIdx);
} else {
// We have it >= 0, i.e., uniform01 equals an entry in prefixSumOfProbabilities.
//
// Because we uniform01 is a random double, the probability of it equalling an endpoint
// in prefixSumOfProbabilities is exceedingly low.
return values.get(it);
}
}
Random Pick Index
Given an array of integers with possible duplicates, randomly output the index of a given target number. You can assume that the given target number must exist in the array.
int[] nums = new int[] {1,2,3,3,3};
Solution solution = new Solution(nums);
// pick(3) should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(3);
// pick(1) should return 0. Since in the array only nums[0] is equal to 1.
solution.pick(1);
You can use HashMap to group together each value with their indices, this will take more space. Another way is to run O(n) random and pick the matched one.
public class RandomPickIndex {
int[] nums;
Random random;
public RandomPickIndex(int[] nums) {
this.nums = nums;
this.random = new Random();
}
public int pick(int target) {
int result = -1;
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == target) {
count++;
if (random.nextInt(count) == 0) {
// don't return here due to nextInt(1) is always zero!
result = i;
}
}
}
return result;
}
}
Random Pick with Weight
Given an array w of positive integers, where w[i] describes the weight of index i, write a function pickIndex which randomly picks an index in proportion to its weight.
Use Prefix Sum and Binary Search.
public class RandomPickWithWeight {
List<Integer> psum = new ArrayList<>();
int tot = 0;
Random rand = new Random();
public RandomPickWithWeight(int[] w) {
for (int x : w) {
tot += x;
psum.add(tot);
}
}
// find the lowest index such that targ < p[x]
public int pickIndex() {
int targ = rand.nextInt(tot);
int lo = 0;
int hi = psum.size() - 1;
while (lo != hi) { // to the same position
int mid = (lo + hi) / 2;
if (targ >= psum.get(mid))
lo = mid + 1;
else
hi = mid;
}
return lo;
}
// or use tree map to get the ceiling value.
public int pickIndex2() {
int key = map.ceilingKey(rand.nextInt(tot) + 1);
// int key= map.heigherKey(rnd.nextInt(cnt));
return map.get(key);
}
}
Random Pick With Blacklist
Given a blacklist B containing unique integers from [0, N), write a function to return a uniform random integer from [0, N) which is NOT in B.
Optimize it such that it minimizes the call to system’s Math.random().
Use virtual whitelist, re-map all blacklist numbers in [0, N - len(B)) to whitelist numbers. Time complexity is O(B) processing. O(1) pick; Space complexity is O(B).
public class RandomPickWithBlacklist {
private Random random;
private int whitelistLen;
private Map<Integer, Integer> map;
public RandomPickWithBlacklist(int N, int[] blacklist) {
map = new HashMap<>();
random = new Random();
whitelistLen = N - blacklist.length;
Set<Integer> set = new LinkedHashSet<>();
for (int i = whitelistLen; i < N; i++)
set.add(i);
for (int b : blacklist) {
if (b >= whitelistLen)
set.remove(b);
}
Iterator<Integer> iterator = set.iterator();
for (int b : blacklist) {
if (b < whitelistLen)
map.put(b, iterator.next());
}
}
public int pick() {
int k = random.nextInt(whitelistLen);
return map.getOrDefault(k, k);
}
}
Find Peak Element
A peak element is an element that is greater than its neighbors.
Given an input array nums, where nums[i] ≠ nums[i+1], find a peak element and return its index.
The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.
You may imagine that nums[-1] = nums[n] = -∞.
Example 1:
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.
public int findPeakElement(int[] nums) {
int l = 0, r = nums.length - 1;
while (l < r) {
int mid = (l + r) / 2;
if (nums[mid] > nums[mid + 1])
r = mid;
else
l = mid + 1;
}
return l;
}
Single Number III
Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.
For example: Given nums = [1, 2, 1, 3, 2, 5], return [3, 5].
We need to do it in two passes: Get the XOR of the two numbers we need to find and locate the LSB; Then use the LSB to divide all numbers to two groups, and find the number in each group.
public int[] singleNumberIII(int[] nums) {
int diff = 0;
for (int num : nums) {
diff ^= num;
}
// Extract the lowest set bit of x which can be used to divide numbers into two groups.
diff &= ~(diff - 1); // or diff &= -diff;
// Each group should have one expected element
int[] result = { 0, 0 };
for (int num : nums) {
if ((num & diff) == 0)
result[0] ^= num;
else
result[1] ^= num;
}
return result;
}
Compute Next Permutation
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).
The replacement must be in-place, do not allocate extra memory.
Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
Solution:
The general algorithm for computing the next permutation is as follows:
- Find k such that p[k] < p[k + 1] and entries after index k appear in decreasing order.
- Find the smallest p[l] (l > k) such that p[l] > p[k].
- Swap p[l] and p[k] (note that the sequence will remain in decreasing order).
- Reverse the sequence after position k.
e.g. 13542 -> 14532 -> 14235
public void nextPermutation(int[] nums) {
if (nums == null || nums.length < 1)
return;
int position = nums.length - 2;
while (position >= 0 && nums[position] >= nums[position + 1]) {
position--;
}
if (position == -1) {
reverse(nums, 0, nums.length - 1);
return;
}
// this position's value should be swapped by the most closed one
for (int i = nums.length - 1; i > position; i--) {
if (nums[i] > nums[position]) {
swap(nums, position, i);
break;
}
}
// reverse all items after the position
reverse(nums, position + 1, nums.length - 1);
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
swap(nums, start++, end--);
}
}
Sudoku Solver
Sudoku is to fill a 9 x 9 grid with digits subject to the constraint that each column, each row, and each of the nine 3 x 3 sub-grids that compose the grid contains unique integers in [1, 9].

We can use recursive style with backtracking.
public void solveSudoku(char[][] board) {
doSolve(board, 0, 0);
}
private boolean doSolve(char[][] board, int row, int col) {
// Note: must reset col here as we need to loop through all rest cells!
for (int i = row; i < 9; i++, col = 0) {
for (int j = col; j < 9; j++) {
if (board[i][j] != '.')
continue;
for (char num = '1'; num <= '9'; num++) {
if (isValid(board, i, j, num)) {
board[i][j] = num;
if (doSolve(board, i, j + 1))
return true;
board[i][j] = '.'; // backtracking
}
}
return false;
}
}
return true;
}
private boolean isValid(char[][] board, int row, int col, char num) {
// Block no. is i/3, first element is i/3*3
int blockRow = (row / 3) * 3, blockCol = (col / 3) * 3;
for (int i = 0; i < 9; i++)
if (board[i][col] == num || board[row][i] == num || board[blockRow + i / 3][blockCol + i % 3] == num)
return false;
return true;
}
Spiral Matrix
Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
For example, Given the following matrix:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
You should return [1,2,3,6,9,8,7,4,5].
// Approach1: Simulation Spiral, always moving right
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> result = new ArrayList<>();
if (matrix.length == 0)
return result;
int[][] shift = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
int m = matrix.length, n = matrix[0].length;
boolean[][] seen = new boolean[m][n];
int row = 0, col = 0, dir = 0;
for (int i = 0; i < m * n; i++) {
result.add(matrix[row][col]);
seen[row][col] = true;
int nextRow = row + shift[dir][0], nextCol = col + shift[dir][1];
// seen[nextRow][nextCol] == true means moving to next right neighbor
if (nextRow < 0 || nextRow >= m || nextCol < 0 || nextCol >= n || seen[nextRow][nextCol]) {
dir = (dir + 1) % 4;
nextRow = row + shift[dir][0];
nextCol = col + shift[dir][1];
}
row = nextRow;
col = nextCol;
}
return result;
}
// Approach2: Layer-by-Layer
public List<Integer> spiralOrder2(int[][] matrix) {
List<Integer> result = new ArrayList<>();
if (matrix.length == 0)
return result;
int r1 = 0, r2 = matrix.length - 1;
int c1 = 0, c2 = matrix[0].length - 1;
while (r1 <= r2 && c1 <= c2) {
for (int c = c1; c <= c2; c++)
result.add(matrix[r1][c]);
r1++;
for (int r = r1; r <= r2; r++)
result.add(matrix[r][c2]);
c2--;
if (r1 <= r2 && c1 <= c2) {
for (int c = c2; c >= c1; c--)
result.add(matrix[r2][c]);
r2--;
for (int r = r2; r >= r1; r--)
result.add(matrix[r][c1]);
c1++;
}
}
return result;
}
Set Matrix Zeroes
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.
Example:
Input:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
Output:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
public void setMatrixZeroes(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return;
int m = matrix.length, n = matrix[0].length;
boolean row = false, col = false;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[0][j] = 0;
matrix[i][0] = 0;
if (i == 0)
row = true;
if (j == 0)
col = true;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0)
matrix[i][j] = 0;
}
}
if (row) {
for (int j = 0; j < n; j++)
matrix[0][j] = 0;
}
if (col) {
for (int i = 0; i < m; i++)
matrix[i][0] = 0;
}
}
Longest Increasing Subsequence
/**
* Given an integer array nums, return the length of the longest strictly increasing subsequence.
*
* A subsequence is a sequence that can be derived from an array by deleting some or no elements
* without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of
* the array [0,3,1,6,2,2,7].
*
* <br>
*
* Example 1:
*
* Input: nums = [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is
* [2,3,7,101], therefore the length is 4.
*
* <br>
*
* Example 2:
*
* Input: nums = [0,1,0,3,2,3] Output: 4
*
* <br>
*
* Example 3:
*
* Input: nums = [7,7,7,7,7,7,7] Output: 1
*
* @author lchen676
*
*/
public class LongestIncreasingSubsequence {
/**
* Intelligently build a pile of subsequences with binary search.
*
* Time complexity: O(Nlog(N))
*/
public int lengthOfLIS(int[] nums) {
List<Integer> sub = new ArrayList<>();
sub.add(nums[0]);
for (int i = 1; i < nums.length; i++) {
int num = nums[i];
if (num > sub.get(sub.size() - 1)) {
sub.add(num);
} else {
int j = binarySearch(sub, num);
sub.set(j, num);
}
}
return sub.size();
}
private int binarySearch(List<Integer> sub, int num) {
int left = 0;
int right = sub.size() - 1;
int mid = (left + right) / 2;
while (left < right) {
mid = (left + right) / 2;
if (sub.get(mid) == num) {
return mid;
}
if (sub.get(mid) < num) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
/**
* Dynamic programming, time complexity: O(N^2)
*
* dp[i] represents the length of the longest increasing subsequence that ends with the element at
* index i.
*/
public int lengthOfLIS2(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int longest = 0;
for (int c : dp) {
longest = Math.max(longest, c);
}
return longest;
}
}
Russian Doll Envelopes
/**
* You are given a 2D array of integers envelopes where envelopes[i] = [wi, hi] represents the width
* and the height of an envelope.
*
* One envelope can fit into another if and only if both the width and height of one envelope are
* greater than the other envelope's width and height.
*
* Return the maximum number of envelopes you can Russian doll (i.e., put one inside the other).
*
* Note: You cannot rotate an envelope.
*
* Example 1:
*
* Input: envelopes = [[5,4],[6,4],[6,7],[2,3]] <br>
* Output: 3 <br>
* Explanation: The maximum number of envelopes you can Russian doll is 3 ([2,3] => [5,4] => [6,7]).
*
* https://leetcode.com/problems/russian-doll-envelopes/
*
*/
public class RussianDollEnvelopes {
public int maxEnvelopes(int[][] envelopes) {
// Check envelopes emptiness if neccessary
// Sort increasing on the first dimension, and decreasing on the second dimension, so that two
// envelopes that are equal in the first dimension can never be in the same increasing subsequence.
Arrays.sort(envelopes, (a, b) -> (a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]));
// dp is an array such that dp[i] is the smallest element that ends an increasing subsequence of
// length i + 1. Whenever we encounter a new element e, we binary search inside dp to find the
// largest index i such that e can end that subsequence. We then update dp[i] with e.
int length = 0;
int dp[] = new int[envelopes.length];
for (int[] envelope : envelopes) {
int height = envelope[1];
if (length == 0 || height > dp[length - 1]) {
dp[length++] = height;
} else {
int index = Arrays.binarySearch(dp, 0, length, height);
dp[index < 0 ? -(index + 1) : index] = height;
}
}
return length;
}
}
Sum of Subarray Minimums
/**
* Given an array of integers arr, find the sum of min(b), where b ranges over every (contiguous)
* subarray of arr. Since the answer may be large, return the answer modulo 10^9 + 7.
*
* <pre>
* Example 1:
*
* Input: arr = [3,1,2,4]
* Output: 17
* Explanation:
* Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4].
* Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1.
* Sum is 17.
* </pre>
*
* https://leetcode.com/problems/sum-of-subarray-minimums/
*/
public class SumofSubarrayMinimums {
// Use monotonic stack to track nums
public int sumSubarrayMins(int[] arr) {
Deque<int[]> stack = new LinkedList<>();
long totalSum = 0, minPreSum = 0;
for (int num : arr) {
int count = 1;
while (!stack.isEmpty() && stack.peek()[0] > num) {
int[] cur = stack.pop();
count += cur[1];
minPreSum -= cur[0] * cur[1]; // deduct invalid numbers
}
stack.push(new int[] { num, count });
minPreSum += count * num;
totalSum += minPreSum;
}
return (int) (totalSum % (1e9 + 7));
}
// Use monotonic stack to track indices
public int sumSubarrayMins2(int[] arr) {
long sum = 0;
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i <= arr.length; i++) {
while (!stack.isEmpty() && (i == arr.length || arr[stack.peek()] > arr[i])) {
int mid = stack.pop(); // middle min pilliar
int left = mid - (stack.isEmpty() ? -1 : stack.peek());
int right = i - mid;
sum += (long) arr[mid] * left * right;
}
stack.push(i);
}
return (int) (sum % (1e9 + 7));
}
// Use monotonic stack to track indices
public int sumSubarrayMins3(int[] arr) {
long sum = 0;
Deque<Integer> stack = new ArrayDeque<>();
stack.push(-1); // leverage a dummy index
for (int i = 0; i <= arr.length; i++) {
while (stack.peek() != -1 && (i == arr.length || arr[stack.peek()] > arr[i])) {
int mid = stack.pop(); // middle min pilliar
int left = mid - stack.peek();
int right = i - mid;
sum += (long) arr[mid] * left * right;
}
stack.push(i);
}
return (int) (sum % (1e9 + 7));
}
}
Subarrays with K Different Integers
/**
* Given an integer array nums and an integer k, return the number of good subarrays of nums.
*
* A good array is an array where the number of different integers in that array is exactly k.
*
* For example, [1,2,3,1,2] has 3 different integers: 1, 2, and 3. A subarray is a contiguous part
* of an array.
*
*
* <pre>
* Example 1:
*
* Input: nums = [1,2,1,2,3], k = 2
* Output: 7
* Explanation: Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2]
* </pre>
*
*/
public class SubarraysWithKDifferentIntegers {
/**
* https://leetcode.com/problems/subarrays-with-k-different-integers/discuss/235235/C%2B%2BJava-with-picture-prefixed-sliding-window
*
* Intuition: If the subarray [left, i] contains K unique numbers, and first prefix numbers also
* appear in [left + prefix, i] subarray, we have total 1 + prefix good subarrays. For example,
* there are 3 unique numers in [1, 2, 1, 2, 3]. First two numbers also appear in the remaining
* subarray [1, 2, 3], so we have 1 + 2 good subarrays: [1, 2, 1, 2, 3], [2, 1, 2, 3] and [1, 2, 3].
*/
public int subarraysWithKDistinct(int[] nums, int k) {
int result = 0, prefix = 0;
int[] counts = new int[nums.length + 1];
int left = 0, count = 0;
for (int i = 0; i < nums.length; i++) {
// Only count for the first time
if (counts[nums[i]]++ == 0) {
count++;
}
// Remove the only left one when exceeded windows size
if (count > k) {
counts[nums[left++]]--;
count--;
prefix = 0;
}
if (count == k) {
// Remove until the number on the left appears only once
while (counts[nums[left]] > 1) {
counts[nums[left++]]--;
prefix++; // increase prefix
}
// Collect all good subarrys
result += prefix + 1;
}
}
return result;
}
}
Game of Life
/**
* Game of Life
*
* https://leetcode.com/problems/game-of-life/
*/
public class GameOfLife {
// Use two bits to preserve the old and new value
public void gameOfLife(int[][] board) {
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int lives = liveNeighbors(board, m, n, i, j);
// Only need to set when the 2nd bit becomes 1.
if (board[i][j] == 1 && lives >= 2 && lives <= 3) {
board[i][j] ^= 1 << 1; // 01 -> 11
}
if (board[i][j] == 0 && lives == 3) {
board[i][j] ^= 1 << 1; // 00 -> 10
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
board[i][j] >>= 1; // Drop the 1st bit
}
}
}
public int liveNeighbors(int[][] board, int m, int n, int i, int j) {
int lives = 0;
for (int x = Math.max(i - 1, 0); x <= Math.min(i + 1, m - 1); x++) {
for (int y = Math.max(j - 1, 0); y <= Math.min(j + 1, n - 1); y++) {
// Skip itself!
if (x != i || y != j) {
lives += board[x][y] & 1;
}
}
}
return lives;
}
}
Minimum Cost For Tickets
/**
*
* Minimum Cost For Tickets
*
* You have planned some train traveling one year in advance. The days of the year in which you will
* travel are given as an integer array days. Each day is an integer from 1 to 365.
*
* Train tickets are sold in three different ways:
*
* a 1-day pass is sold for costs[0] dollars, a 7-day pass is sold for costs[1] dollars, and a
* 30-day pass is sold for costs[2] dollars. The passes allow that many days of consecutive travel.
*
* For example, if we get a 7-day pass on day 2, then we can travel for 7 days: 2, 3, 4, 5, 6, 7,
* and 8. Return the minimum number of dollars you need to travel every day in the given list of
* days.
*
* <pre>
* Example 1:
*
* Input: days = [1,4,6,7,8,20], costs = [2,7,15]
* Output: 11
* Explanation: For example, here is one way to buy passes that lets you travel your travel plan:
* On day 1, you bought a 1-day pass for costs[0] = $2, which covered day 1.
* On day 3, you bought a 7-day pass for costs[1] = $7, which covered days 3, 4, ..., 9.
* On day 20, you bought a 1-day pass for costs[0] = $2, which covered day 20.
* In total, you spent $11 and covered all the days of your travel.
* </pre>
*
*
* https://leetcode.com/problems/minimum-cost-for-tickets/
*
*/
public class MinimumCostForTickets {
public int mincostTickets(int[] days, int[] costs) {
int[] durations = { 1, 7, 30 }; // 3 different ways
return recursiveDP(days, costs, durations, 0, new int[days.length]);
}
public int recursiveDP(int[] days, int[] costs, int[] durations, int i, int[] memo) {
if (i >= days.length) {
return 0;
}
if (memo[i] != 0) {
return memo[i];
}
int ans = Integer.MAX_VALUE, j = i;
for (int d = 0; d < durations.length; d++) {
while (j < days.length && days[j] < days[i] + durations[d]) {
j++;
}
ans = Math.min(ans, recursiveDP(days, costs, durations, j, memo) + costs[d]);
}
memo[i] = ans;
return ans;
}
}
String Boot Camp
Sheet Column Encoding
Implement a function that converts a spreadsheet column id to the corresponding integer. For example, 4 for “D”, 27 for “AA”, 702 for “ZZ”, etc.
public int decodeColumnId(String colId) {
int result = 0;
for (int i = 0; i < colId.length(); i++) {
result = result * 26 + (colId.charAt(i) - 'A' + 1);
}
return result;
}
Reverse Words
Given an input string, reverse the string word by word. A word is defined as a sequence of non-space characters. The input string does not contain leading or trailing spaces and the words are always separated by a single space. For example, Given s = “the sky is blue”, return “blue is sky the”.
public void reverseWords(char[] str) {
reverse(str, 0, str.length - 1);
int start = 0, end = 0;
while (end < str.length) {
if (str[end] == ' ') {
reverse(str, start, end - 1);
start = end + 1;
}
end++;
}
reverse(str, start, end - 1);
}
private void reverse(char[] str, int start, int end) {
while (start < end) {
char tmp = str[start];
str[start] = str[end];
str[end] = tmp;
start++;
end--;
}
}
Word Break
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.
Example 2:
Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.
NOTE: There could be multiple ways to break word, in industry, also need to consider the context, category, culture etc to pick up the most suitable one! You should even choose different dictionaries which might have ranking for each words. To support multiple languages, we need use unicode as well, to avoid excessive space cost associated with R-way tries, consider using TST (Ternary Search Tree).
// Recursion with memoization
public boolean wordBreak1(String s, List<String> wordDict) {
return wordBreak1(s, new HashSet<String>(wordDict), 0, new Boolean[s.length()]);
}
public boolean wordBreak1(String s, Set<String> wordDict, int start, Boolean[] memo) {
if (start == s.length())
return true;
if (memo[start] != null)
return memo[start];
for (int end = start + 1; end <= s.length(); end++) {
if (wordDict.contains(s.substring(start, end)) && wordBreak1(s, wordDict, end, memo))
return memo[start] = true;
}
return memo[start] = false;
}
// Use Breadth-First-Search
public boolean wordBreak2(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet<>(wordDict);
Queue<Integer> queue = new LinkedList<>();
int[] visited = new int[s.length()];
queue.add(0);
while (!queue.isEmpty()) {
int start = queue.remove();
if (visited[start] == 0) {
for (int end = start + 1; end <= s.length(); end++) {
if (wordDictSet.contains(s.substring(start, end))) {
queue.add(end);
if (end == s.length())
return true;
}
}
visited[start] = 1;
}
}
return false;
}
// Dynamic programming
public boolean wordBreak3(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet<>(wordDict);
boolean[] found = new boolean[s.length() + 1];
found[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (found[j] && wordDictSet.contains(s.substring(j, i))) {
found[i] = true;
break;
}
}
}
return found[s.length()];
}
// Also can apply Trie Tree (or TST) to break earlier (if there were many words to check)
// Can also resolve the question: Concatenated Words
// A word can only be formed by words shorter than it. So we can first sort the input
// by length of each word, and only try to form one word by using words in front of it.
public List<String> findAllConcatenateWords(String[] words) {
List<String> result = new ArrayList<>();
Set<String> preWords = new HashSet<>();
Arrays.sort(words, (a, b) -> (a.length() - b.length()));
for (String word : words) {
if (canForm(word, preWords))
result.add(word);
preWords.add(word);
}
return result;
}
private static boolean canForm(String word, Set<String> dict) {
if (dict.isEmpty())
return false;
boolean[] dp = new boolean[word.length() + 1];
dp[0] = true;
for (int i = 1; i <= word.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[i] && dict.contains(word.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[word.length()];
}
Word Break II
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences.
Sample:
Input:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
Output:
[
"cats and dog",
"cat sand dog"
]
Solution: Use recursion with memoization, time and space complexity are all O(n^3).
public class WordBreak {
public static List<String> wordBreak(String input, List<String> wordDict) {
List<String> result = new ArrayList<>();
if (input.length() == 0 || wordDict.isEmpty())
return result;
int minLen = Integer.MAX_VALUE, maxLen = Integer.MIN_VALUE;
Set<String> wordSet = new HashSet<>();
for (String word : wordDict) {
wordSet.add(word);
minLen = Math.min(minLen, word.length());
maxLen = Math.max(maxLen, word.length());
}
StringBuilder sentence = new StringBuilder();
boolean[] failed = new boolean[input.length()]; // failed memo
wordBreak(input, wordSet, minLen, maxLen, 0, failed, sentence, result);
return result;
}
private static boolean wordBreak(String input, Set<String> wordSet, int minLen, int maxLen, int start,
boolean[] failed, StringBuilder sentence, List<String> result) {
if (start == input.length()) {
sentence.setLength(sentence.length() - 1);
result.add(sentence.toString());
return true;
}
// break ealier
if (failed[start])
return false;
boolean succeed = false;
for (int i = start + minLen - 1; i < Math.min(input.length(), start + maxLen); i++) {
String sub = input.substring(start, i + 1);
if (wordSet.contains(sub)) {
int sLen = sentence.length();
sentence.append(sub).append(' ');
if (wordBreak(input, wordSet, minLen, maxLen, i + 1, failed, sentence, result))
succeed = true;
sentence.setLength(sLen); // back track
}
}
failed[start] = !succeed;
return succeed;
}
public static void main(String[] args) {
String s = "pineapplepenapple";
List<String> wordDict = Arrays.asList("apple", "pen", "applepen", "pine", "pineapple");
assert wordBreak(s, wordDict).toString()
.equals("[pine apple pen apple, pine applepen apple, pineapple pen apple]");
}
}
Repeated DNA Sequence
All DNA is composed of a series of nucleotides abbreviated as A, C, G, and T, for example: “ACGAATTCCG”. When studying DNA, it is sometimes useful to identify repeated sequences within the DNA.
Write a function to find all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule.
Example: Input: s = “AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT” Output: [“AAAAACCCCC”, “CCCCCAAAAA”]
public List<String> findRepeatedDnaSequences(String s) {
List<String> res = new ArrayList<>();
if (s == null || s.length() < 10)
return res;
Set<String> set = new HashSet<>();
Set<String> ans = new HashSet<>();
for (int i = 0; i < s.length() - 9; i++) {
String temp = s.substring(i, i + 10);
if (set.contains(temp)) {
ans.add(temp);
} else {
set.add(temp);
}
}
res.addAll(ans);
return res;
}
Custom Sort String
S and T are strings composed of lowercase letters. In S, no letter occurs more than once.
S was sorted in some custom order previously. We want to permute the characters of T so that they match the order that S was sorted. More specifically, if x occurs before y in S, then x should occur before y in the returned string.
Solution: Count and Write
public String customSortString(String S, String T) {
int[] count = new int[26];
for (char c : T.toCharArray())
count[c - 'a']++;
StringBuilder sb = new StringBuilder();
for (char c : S.toCharArray()) {
for (int i = 0; i < count[c - 'a']; i++)
sb.append(c);
count[c - 'a'] = 0;
}
// add the rest letters
for (char c = 'a'; c <= 'z'; c++) {
for (int i = 0; i < count[c - 'a']; i++)
sb.append(c);
}
return sb.toString();
}
Replace and Remove
Given an array of characters, and remove each b and replaces each a by two ds. You can assume the array has enough space to hold the final result.
We can first delete bs and compute the final number of valid characters of the string.
It’s important to delete b first as it will help to shrink the size first!
public int replaceAndRemove(int size, char[] s) {
int writeIdx = 0, aCount = 0;
for (int i = 0; i < size; i++) {
if (s[i] != 'b')
s[writeIdx++] = s[i];
if (s[i] == 'a')
aCount++;
}
int curIdx = writeIdx - 1;
writeIdx += aCount - 1;
final int finalSize = writeIdx + 1;
while (curIdx >= 0) {
if (s[curIdx] == 'a') {
s[writeIdx--] = 'd';
s[writeIdx--] = 'd';
} else {
s[writeIdx--] = s[curIdx];
}
curIdx--;
}
return finalSize;
}
Group Shifted Strings
Given a string, we can “shift” each of its letter to its successive letter, for example: “abc” -> “bcd”. We can keep “shifting” which forms the sequence:
“abc” -> “bcd” -> … -> “xyz” Given a list of strings which contains only lowercase alphabets, group all strings that belong to the same shifting sequence.
Example:
Input: ["abc", "bcd", "acef", "xyz", "az", "ba", "a", "z"],
Output:
[
["abc","bcd","xyz"],
["az","ba"],
["acef"],
["a","z"]
]
public List<List<String>> groupStrings(String[] strings) {
Map<String, List<String>> patternGroups = new HashMap<>();
for (String str : strings) {
String pattern = generatePattern(str);
List<String> currentGroup = patternGroups.getOrDefault(pattern, new ArrayList<>());
patternGroups.put(pattern, currentGroup);
currentGroup.add(str);
}
List<List<String>> result = new ArrayList<>();
for (List<String> group : patternGroups.values())
result.add(group);
return result;
}
private String generatePattern(String str) {
StringBuilder pattern = new StringBuilder();
int n = str.length();
for (int i = 1; i < n; i++) {
// use s[i]-s[i-1] can also handle different shitting steps
// e.g. the first letter shift 1 step, second 2 steps...
int diff = str.charAt(i) - str.charAt(i - 1);
if (diff < 0)
diff += 26;
pattern.append(diff);
if (i < n - 1)
pattern.append("-");
}
return pattern.toString();
}
Compare Version Numbers
Compare two version numbers version1 and version2. If version1 > version2 return 1; if version1 < version2 return -1;otherwise return 0.
You may assume that the version strings are non-empty and contain only digits and the . character. The . character does not represent a decimal point and is used to separate number sequences. For instance, 2.5 is not “two and a half” or “half way to version three”, it is the fifth second-level revision of the second first-level revision.
Example 1:
Input: version1 = "0.1", version2 = "1.1"; Output: -1
Input: version1 = "7.5.2.4", version2 = "7.5.3"; Output: -1
public int compareVersion(String version1, String version2) {
int l1 = version1.length(), l2 = version2.length();
int i = 0, j = 0;
while (i < l1 || j < l2) {
int num1 = 0, num2 = 0;
while (i < l1 && version1.charAt(i) != '.') {
num1 = num1 * 10 + version1.charAt(i++) - '0';
}
while (j < l2 && version2.charAt(j) != '.') {
num2 = num2 * 10 + version2.charAt(j++) - '0';
}
if (num1 > num2)
return 1;
else if (num1 < num2)
return -1;
else {
i++;
j++;
}
}
return 0;
}
Find First Substring
Given two strings s (the search string) and t (the text), find the first occurrence of s in t.
We can use Rabin-Karp algorithm to do the linear time string matching, we need a good hash function, to reduce the likelihood of collisions, which entail potentially time consuming string equality checks.
public int rabinKarp(String t, String s) {
if (s.length() > t.length())
return -1; // s is not a substring of t.
final int BASE = 26;
int tHash = 0, sHash = 0; // Hash codes for the substring of t and s.
int powerS = 1; // BASE^|s-1|.
for (int i = 0; i < s.length(); i++) {
powerS = i > 0 ? powerS * BASE : 1;
tHash = tHash * BASE + t.charAt(i);
sHash = sHash * BASE + s.charAt(i);
}
for (int i = 0; i <= t.length() - s.length(); i++) {
// Compare two strings to protest again hash collision!
if (tHash == sHash && t.substring(i, i + s.length()).equals(s))
return i;
// Efficiently calculate next hash from current hash
tHash -= t.charAt(i) * powerS;
tHash = tHash * BASE + t.charAt(i + s.length());
}
return -1; // s is not a substring of t.
}
Shortest Word Distance
Design a class which receives a list of words in the constructor, and implements a method that takes two words word1 and word2 and return the shortest distance between these two words in the list. Your method will be called repeatedly many times with different parameters.
Example: Assume that words = [“practice”, “makes”, “perfect”, “coding”, “makes”].
Input: word1 = “coding”, word2 = “practice” Output: 3 Input: word1 = “makes”, word2 = “coding” Output: 1
public class WordDistance {
Map<String, List<Integer>> map;
public WordDistance(String[] words) {
map = new HashMap<String, List<Integer>>();
for (int i = 0; i < words.length; i++) {
List<Integer> list = map.getOrDefault(words[i], new ArrayList<Integer>());
list.add(i);
map.put(words[i], list);
}
}
public int shortest(String word1, String word2) {
List<Integer> list1 = map.getOrDefault(word1, new ArrayList<>());
List<Integer> list2 = map.getOrDefault(word2, new ArrayList<>());
int i = 0, j = 0;
int shortest = Integer.MAX_VALUE;
while (i < list1.size() && j < list2.size()) {
int a = list1.get(i);
int b = list2.get(j);
shortest = Math.min(shortest, Math.abs(b - a));
if (a < b)
i++;
else if (a > b)
j++;
}
return shortest;
}
}
Decode Nested String
Given an encoded string, return it’s decoded string.
The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.
Examples:
s = "3[a]2[bc]", return "aaabcbc".
s = "3[a2[c]]", return "accaccacc".
s = "2[abc]3[cd]ef", return "abcabccdcdcdef".
public String decodeString(String s) {
Deque<Integer> count = new LinkedList<>();
Deque<String> result = new LinkedList<>();
int i = 0;
result.push("");
while (i < s.length()) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
int start = i;
while (Character.isDigit(s.charAt(i + 1)))
i++;
count.push(Integer.valueOf(s.substring(start, i + 1)));
} else if (c == '[') {
result.push("");
} else if (c == ']') {
String sub = result.pop();
StringBuilder sb = new StringBuilder();
int times = count.pop();
for (int j = 0; j < times; j += 1) {
sb.append(sub);
}
result.push(result.pop() + sb.toString());
} else {
result.push(result.pop() + c);
}
i++;
}
return result.pop();
}
Similar String Groups
Two strings X and Y are similar if we can swap two letters (in different positions) of X, so that it equals Y.
For example, “tars” and “rats” are similar (swapping at positions 0 and 2), and “rats” and “arts” are similar, but “star” is not similar to “tars”, “rats”, or “arts”.
Together, these form two connected groups by similarity: {“tars”, “rats”, “arts”} and {“star”}. Notice that “tars” and “arts” are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list A of strings. Every string in A is an anagram of every other string in A. How many groups are there?
Example 1:
Input: [“tars”,”rats”,”arts”,”star”] Output: 2
public int numSimilarGroups(String[] A) {
if (A == null || A.length == 0)
return 0;
int count = 0;
boolean[] visited = new boolean[A.length];
for (int i = 0; i < A.length; i++) {
if (!visited[i]) {
visited[i] = true;
dfs(A, A[i], visited);
count++;
}
}
return count;
}
private void dfs(String[] A, String str, boolean[] visited) {
for (int i = 0; i < A.length; i++) {
if (!visited[i] && isDiffBy2(str, A[i])) {
visited[i] = true;
dfs(A, A[i], visited);
}
}
}
private boolean isDiffBy2(String str1, String str2) {
if (str1.length() != str2.length())
return false;
int diff = 0;
for (int i = 0; i < str1.length(); i++) {
if (str1.charAt(i) != str2.charAt(i))
diff++;
if (diff > 2)
return false;
}
return true;
}
K-Similar Strings
Strings A and B are K-similar (for some non-negative integer K) if we can swap the positions of two letters in A exactly K times so that the resulting string equals B.
Given two anagrams A and B, return the smallest K for which A and B are K-similar.
Example 1:
Input: A = "abc", B = "bca"
Output: 2
Example 2:
Input: A = "abac", B = "baca"
Output: 2
Example 3:
Input: A = "aabc", B = "abca"
Output: 2
public int kSimilarity(String source, String target) {
Queue<String> queue = new ArrayDeque<>();
queue.offer(source);
Map<String, Integer> distances = new HashMap<>();
distances.put(source, 0);
while (!queue.isEmpty()) {
String word = queue.poll();
if (word.equals(target))
return distances.get(word);
for (String neighbor : neighbors(word, target)) {
if (!distances.containsKey(neighbor)) {
distances.put(neighbor, distances.get(word) + 1);
queue.offer(neighbor);
}
}
}
return 0;
}
public List<String> neighbors(String source, String target) {
List<String> ans = new ArrayList<>();
int i = 0;
while (i < source.length() && source.charAt(i) == target.charAt(i)) {
i++;
}
char[] neighbor = source.toCharArray();
for (int j = i + 1; j < source.length(); j++) {
if (source.charAt(j) == target.charAt(i)) {
swap(neighbor, i, j);
ans.add(new String(neighbor));
swap(neighbor, i, j);
}
}
return ans;
}
public void swap(char[] s, int i, int j) {
char t = s[i];
s[i] = s[j];
s[j] = t;
}
Add/Multiply Strings
Given two non-negative integers num1 and num2 represented as string, return the sum of num1 and num2. Given two non-negative integers num1 and num2 represented as strings, return the product of num1 and num2. Note: The length of both num1 and num2 is < 5100. Both num1 and num2 contains only digits 0-9. Both num1 and num2 does not contain any leading zero. You must not use any built-in BigInteger library or convert the inputs to integer directly.
We can use grade-school algorithm for multiplication which consists of multiplying the first number by each digit of the second, and then adding all the resulting terms.
public String addStrings(String num1, String num2) {
StringBuilder sb = new StringBuilder();
int carry = 0;
for (int i = num1.length() - 1, j = num2.length() - 1; i >= 0 || j >= 0; i--, j--) {
int sum = carry;
if (i >= 0)
sum += num1.charAt(i) - '0';
if (j >= 0)
sum += num2.charAt(j) - '0';
sb.append(sum % 10);
carry = sum / 10;
}
if (carry > 0)
sb.append(carry);
return sb.reverse().toString();
}
public String multiplyStrings(String num1, String num2) {
int m = num1.length(), n = num2.length();
int[] pos = new int[m + n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
int p1 = i + j, p2 = i + j + 1;
int sum = mul + pos[p2];
pos[p1] += sum / 10;
pos[p2] = sum % 10;
}
}
StringBuilder sb = new StringBuilder();
for (int p : pos) {
if (sb.length() == 0 && p == 0)
continue;
sb.append(p);
}
return sb.length() == 0 ? "0" : sb.toString();
}
Reorganize String
/**
* Given a string s, rearrange the characters of s so that any two adjacent characters are not the
* same. Return any possible rearrangement of s or return "" if not possible.
*
* Example 1: Input: s = "aab" Output: "aba"
*
*/
public String reorganizeString(String s) {
// count characters
int[] counts = new int[26];
for (int i = 0; i < s.length(); i++) {
counts[s.charAt(i) - 'a']++;
}
int maxChar = 0;
for (int i = 0; i < counts.length; i++) {
if (counts[i] > counts[maxChar]) {
maxChar = i;
}
}
if (counts[maxChar] > (s.length() + 1) / 2) {
return ""; // not possible
}
// reorganize string
int idx = 0;
char[] chars = new char[s.length()];
for (int i = 0; i < counts[maxChar]; i++) {
chars[idx] = (char) (maxChar + 'a');
idx += 2;
}
counts[maxChar] = 0; // update to 0
for (int i = 0; i < counts.length; i++) {
for (int j = 0; j < counts[i]; j++) {
if (idx >= chars.length) {
idx = 1;
}
chars[idx] = (char) (i + 'a');
idx += 2;
}
counts[i] = 0;
}
return new String(chars);
}
/**
* Given a string s and an integer k, rearrange s such that the same characters are at least
* distance k from each other. If it is not possible to rearrange the string, return an empty string
* "".
*
* Example 1: Input: s = "aabbcc", k = 3 Output: "abcabc" Explanation: The same letters are at least
* a distance of 3 from each other.
*
* Example 2: Input: s = "aaadbbcc", k = 2 Output: "abacabcd" Explanation: The same letters are at
* least a distance of 2 from each other.
*/
public String rearrangeString(String s, int k) {
if (k == 0) {
return s;
}
int[][] counts = new int[26][2];
for (int i = 0; i < 26; i++) {
counts[i] = new int[] { i, 0 };
}
for (char c : s.toCharArray()) {
counts[c - 'a'][1]++;
}
Arrays.sort(counts, (a, b) -> (b[1] - a[1]));
int largestDuplicate = 1;
for (int i = 1; i < counts.length; i++) {
if (counts[i][1] == counts[i - 1][1]) {
largestDuplicate++;
} else {
break;
}
}
if (s.length() < (counts[0][1] - 1) * k + largestDuplicate) {
return "";
}
char[] chars = new char[s.length()];
int pairIndex = 0, stringOffset = s.length() % k - 1;
stringOffset = stringOffset < 0 ? stringOffset + k : stringOffset;
int stringIndex = stringOffset;
for (int i = 0; i < s.length(); i++) {
if (counts[pairIndex][1] == 0) {
pairIndex++;
}
if (stringIndex >= s.length()) {
stringOffset--;
if (stringOffset < 0) {
stringOffset += k;
}
stringIndex = stringOffset;
}
chars[stringIndex] = (char) ('a' + counts[pairIndex][0]);
counts[pairIndex][1]--;
stringIndex += k;
}
return new String(chars);
}
// Use priority queue
public String rearrangeString2(String s, int k) {
if (k == 0) {
return s;
}
int[] counts = new int[26];
for (int i = 0; i < s.length(); i++) {
counts[s.charAt(i) - 'a']++;
}
Queue<Character> queue = new PriorityQueue<>((a, b) -> (counts[b - 'a'] - counts[a - 'a']));
for (int i = 0; i < counts.length; i++) {
if (counts[i] != 0) {
queue.add((char) (i + 'a'));
}
}
StringBuilder builder = new StringBuilder();
while (!queue.isEmpty()) {
char c = queue.poll();
builder.append(c);
counts[c - 'a']--;
// look back k distance and put back if applicable
if (builder.length() >= k) {
c = builder.charAt(builder.length() - k);
if (counts[c - 'a'] > 0) {
queue.add(c);
}
}
}
return builder.length() != s.length() ? "" : builder.toString();
}
Buy and Sell Stock
Max Profit With Single Transaction
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Example 1: Input: [7, 1, 5, 3, 6, 4] Output: 5 max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price) Example 2: Input: [7, 6, 4, 3, 1] Output: 0 In this case, no transaction is done, i.e. max profit = 0.
// track min price, and also cover minimum lose
public int maxProfitWithSingleTransaction(int[] prices) {
if (prices.length < 2)
return 0;
int minPrice = Integer.MAX_VALUE, maxProfit = Integer.MIN_VALUE;
for (int price : prices) {
maxProfit = Math.max(maxProfit, price - minPrice);
minPrice = Math.min(minPrice, price);
}
return maxProfit;
}
// track max current and also cover minimum lose
public int maxProfitWithSingleTransaction2(int[] prices) {
if (prices.length < 2)
return 0;
int maxCur = Integer.MIN_VALUE, maxSoFar = Integer.MIN_VALUE;
for (int i = 1; i < prices.length; i++) {
int diff = prices[i] - prices[i - 1];
maxCur = maxCur >= 0 ? maxCur + diff : diff;
maxSoFar = Math.max(maxCur, maxSoFar);
}
return maxSoFar;
}
Max Profit With Max 2 Transaction
Assume we have 0 money at first, use 4 variables to maintain ceilings so far.
public int maxProfitWithMax2Transactions(int[] prices) {
int buy1 = Integer.MIN_VALUE, sell1 = 0;
int buy2 = Integer.MIN_VALUE, sell2 = 0;
for (int i = 0; i < prices.length; i++) {
buy1 = Math.max(buy1, 0 - prices[i]);
sell1 = Math.max(sell1, buy1 + prices[i]);
buy2 = Math.max(buy2, sell1 - prices[i]);
sell2 = Math.max(sell2, buy2 + prices[i]);
}
return sell2;
}
// This solution is tracking forward and backward
public int maxProfitWithMax2Transactions2(int[] prices) {
int maxProfit = 0;
int[] firstBuySellProfits = new int[prices.length];
// forward path
int minPrice = Integer.MAX_VALUE;
for (int i = 0; i < prices.length; i++) {
minPrice = Math.min(minPrice, prices[i]);
maxProfit = Math.max(maxProfit, prices[i] - minPrice);
firstBuySellProfits[i] = maxProfit;
}
// backward path
int maxPrice = Integer.MIN_VALUE;
for (int i = prices.length - 1; i > 0; i--) {
maxPrice = Math.max(maxPrice, prices[i]);
maxProfit = Math.max(maxProfit, maxPrice - prices[i] + firstBuySellProfits[i - 1]);
}
return maxProfit;
}
Max Profit With Max K Transactions
/*
* DP to store the previous result to reduce redundant calculations.
* (k >= len / 2) means we will not reach the limit no matter how we try, can simply deal as max transactions.
* Time Complexity: O(nk) if 2k ≤ n, O(n) if 2k > n where n is the length of the prices sequence, since we have two for-loop.
* Space Complexity: O(nk) without state-compressed, and O(k) with state-compressed, where n is the length of the prices sequence.
*/
public int maxProfitWithMaxKTransactions(int k, int[] prices) {
int len = prices.length;
if (k >= len / 2)
return quickSolve(prices);
// Cash after n <= k transactions at this price
int[][] t = new int[k + 1][len];
for (int i = 1; i <= k; i++) {
int buyMax = 0 - prices[0];
for (int j = 1; j < len; j++) {
// To sell at current price
t[i][j] = Math.max(t[i][j - 1], buyMax + prices[j]);
// To buy at current price for next transaction
buyMax = Math.max(buyMax, t[i - 1][j - 1] - prices[j]);
}
}
return t[k][len - 1];
}
public int maxProfitWithMaxKTransactions2(int k, int[] prices) {
int len = prices.length;
if (k >= len / 2)
return quickSolve(prices);
int[] minPrices = new int[k + 1];
Arrays.fill(minPrices, Integer.MAX_VALUE);
int[] maxProfits = new int[k + 1];
for (int price : prices) {
for (int i = k; i > 0; i--) {
maxProfits[i] = Math.max(maxProfits[i], price - minPrices[i]);
minPrices[i] = Math.min(minPrices[i], price - (i > 0 ? maxProfits[i - 1] : 0));
}
}
return maxProfits[maxProfits.length - 1];
}
private int quickSolve(int[] prices) {
int len = prices.length, profit = 0;
for (int i = 1; i < len; i++) {
if (prices[i] > prices[i - 1])
profit += prices[i] - prices[i - 1];
}
return profit;
}
Max Profit with Max Transactions
/*
* Simple One Pass: Crawling over the slope and keep on adding the profit obtained from every consecutive transaction.
*/
public int maxProfitWithMaxTransactions(int[] prices) {
int maxProfit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
return maxProfit;
}
/*
* Peak Valley Approach: The key point is we need to consider every peak immediately following a valley to maximize the profit.
*/
public int maxProfitWithMaxTransactions2(int[] prices) {
int i = 0;
int valley = prices[0];
int peak = prices[0];
int maxProfit = 0;
while (i < prices.length - 1) {
while (i < prices.length - 1 && prices[i] >= prices[i + 1])
i++;
valley = prices[i];
while (i < prices.length - 1 && prices[i] <= prices[i + 1])
i++;
peak = prices[i];
maxProfit += peak - valley;
}
return maxProfit;
}
/*
* Best Time to Buy and Sell Stock with Transaction Fee
*/
public int maxProfitWithMaxTransactionsAndFee(int[] prices, int fee) {
int sell = 0, buy = Integer.MIN_VALUE;
for (int price : prices) {
buy = Math.max(buy, sell - price);
sell = Math.max(sell, buy + price - fee);
}
return sell;
}
/*
* To transition from the i-th day to the i+1-th day, we either sell our stock
* cash = max(cash, hold + prices[i] - fee) or buy a stock hold = max(hold, cash - prices[i]).
* At the end, we want to return cash. We can transform cash first without using temporary
* variables because selling and buying on the same day can't be better than just
* continuing to hold the stock.
*/
public int maxProfitWithMaxTransactionsAndFee2(int[] prices, int fee) {
int cash = 0; // max profit if we sell in past
int hold = -prices[0]; // max profit if we buy in past
for (int i = 1; i < prices.length; i++) {
cash = Math.max(cash, hold + prices[i] - fee); // Let's sell and find max profit
hold = Math.max(hold, cash - prices[i]); // Let's buy and find max profit
}
return cash;
}
/**
* Best Time to Buy and Sell Stock with Cooldown
*/
public int maxProfitWithMaxTransactionsAndCooldown(int[] prices) {
int sell = 0, prevSell = 0;
int buy = Integer.MIN_VALUE, prevBuy = 0;
for (int price : prices) {
prevBuy = buy; // Preserve past buy
buy = Math.max(buy, prevSell - price);
prevSell = sell; // Preserve past sell
sell = Math.max(sell, prevBuy + price);
}
return sell;
}
/**
* Given a list stock prices (i.e. price[0...n]), our agent would walk through each price point one
* by one. At each point, the agent would be in one of three states (i.e. held, sold and reset) that
* we defined before. And at each point, the agent would take one of the three actions (i.e. buy,
* sell and rest), which then would lead to the next state at the next price point.
*/
public int maxProfitWithMaxTransactionsAndCooldown2(int[] prices) {
int sold = Integer.MIN_VALUE, held = Integer.MIN_VALUE, reset = 0;
for (int price : prices) {
int preSold = sold;
sold = held + price;
held = Math.max(held, reset - price);
reset = Math.max(reset, preSold);
}
return Math.max(sold, reset);
}
Substring Search
| algorithm | version | guarantee | typical | backup in input? | correct? | extra space |
|---|---|---|---|---|---|---|
| brute force | - | \(mn\) | \(1.1n\) | yes | yes | \(1\) |
| Knuth-Morris-Pratt | full DFA | \(2n\) | \(1.1n\) | no | yes | \(mR\) |
| Knuth-Morris-Pratt | mismatch transitions only | \(3n\) | \(1.1n\) | no | yes | \(m\) |
| Boyer-Moore | full algorithm | \(3n\) | \(n/m\) | yes | yes | \(R\) |
| Boyer-Moore | mismatched char heuristic only | \(mn\) | \(n/m\) | yes | yes | \(R\) |
| Rabin-Karp | Monte Carlo | \(7n\) | \(7n\) | no | yes | \(1\) |
| Rabin-Karp | Las Vegas | \(7n\) | \(7n\) | yes | yes | \(1\) |
Brute-force substring search
public static int search(String pat, String txt) {
int m = pat.length();
int n = txt.length();
for (int i = 0; i <= n - m; i++) {
int j = 0;
for (j = 0; j < m; j++) {
if (txt.charAt(i + j) != pat.charAt(j)) {
break;
}
}
if (j == m) return i; // found;
}
return n; // not found
}
// Alternate implementation
public static int search(String pat, String txt) {
int j, m = pat.length();
int i, n = txt.length();
for (i = 0, j = 0; i < n && j < m; i++) {
if (txt.charAt(i) == pat.charAt(j))
j++;
else {
i -= j; // back up
j = 0;
}
}
if (j == m)
return i - m; // found
else
return n; // not found
}
Knuth-Morris-Pratt substring search
Whenever detect a mismatch, you already know some of the characters in the text (since they matched the pattern characters prior to the mismatch). We can take advantage of this information to avoid backing up the text pointer over all those characters.
A useful to describe this process is in terms of a deterministic finite-state automaton (DFA).
Key differences from brute-force implementation:
- Need to precompute
dfa[][]from pattern. - Text pointer i never decrements.
- Could use input stream.
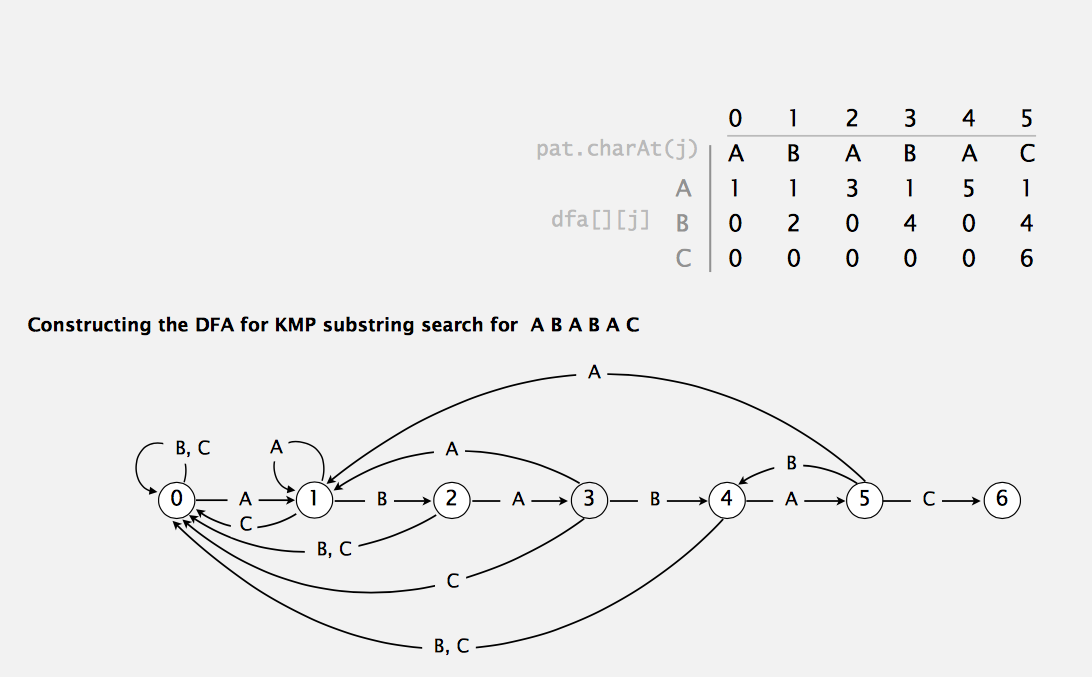
public class KMP {
private final int R; // the radix
private int[][] dfa; // the KMP automoton
private char[] pattern; // either the character array for the pattern
private String pat; // or the pattern string
/**
* Preprocesses the pattern string.
*
* @param pat
* the pattern string
*/
public KMP(String pat) {
this.R = 256;
this.pat = pat;
// build DFA from pattern
int m = pat.length();
dfa = new int[R][m];
dfa[pat.charAt(0)][0] = 1;
for (int x = 0, j = 1; j < m; j++) {
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][x]; // Copy mismatch cases.
dfa[pat.charAt(j)][j] = j + 1; // Set match case.
x = dfa[pat.charAt(j)][x]; // Update restart state.
}
}
/**
* Preprocesses the pattern string.
*
* @param pattern
* the pattern string
* @param R
* the alphabet size
*/
public KMP(char[] pattern, int R) {
this.R = R;
this.pattern = new char[pattern.length];
for (int j = 0; j < pattern.length; j++)
this.pattern[j] = pattern[j];
// build DFA from pattern
int m = pattern.length;
dfa = new int[R][m];
dfa[pattern[0]][0] = 1;
for (int x = 0, j = 1; j < m; j++) {
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][x]; // Copy mismatch cases.
dfa[pattern[j]][j] = j + 1; // Set match case.
x = dfa[pattern[j]][x]; // Update restart state.
}
}
/**
* Returns the index of the first occurrrence of the pattern string in the text string.
*
* @param txt
* the text string
* @return the index of the first occurrence of the pattern string in the text string; N if no
* such match
*/
public int search(String txt) {
// simulate operation of DFA on text
int m = pat.length();
int n = txt.length();
int i, j;
for (i = 0, j = 0; i < n && j < m; i++) {
j = dfa[txt.charAt(i)][j];
}
if (j == m)
return i - m; // found
return n; // not found
}
/**
* Returns the index of the first occurrrence of the pattern string in the text string.
*
* @param text
* the text string
* @return the index of the first occurrence of the pattern string in the text string; N if no
* such match
*/
public int search(char[] text) {
// simulate operation of DFA on text
int m = pattern.length;
int n = text.length;
int i, j;
for (i = 0, j = 0; i < n && j < m; i++) {
j = dfa[text[i]][j];
}
if (j == m)
return i - m; // found
return n; // not found
}
// Could use input stream without the need to backup input.
public int search(In in) {
int m = pattern.length;
int i, j;
for (i = 0, j = 0; !in.isEmpty() && j < m; i++) {
j = dfa[in.readChar()][j];
}
if (j == m)
return i - m;
else
return NOT_FOUND;
}
}
Boyer-Moore substring search
When backup in the text string is not a problem, we can develop a significantly faster substring-searching method by scanning the pattern from right to left when trying to match it against the text.
To implement the mismatched character heuristic, we use an pre-computed array right[] that gives, the index of its rightmost occurrence in the pattern (-1 if the character is not in the pattern).
- Scan characters in pattern from right to left;
- Can skip as many as M text chars when finding one not in the pattern.

public class BoyerMoore {
private final int R; // the radix
private int[] right; // the bad-character skip array
private char[] pattern; // store the pattern as a character array
private String pat; // or as a string
/**
* Preprocesses the pattern string.
*
* @param pat
* the pattern string
*/
public BoyerMoore(String pat) {
this.R = 256;
this.pat = pat;
// position of rightmost occurrence of c in the pattern
right = new int[R];
for (int c = 0; c < R; c++)
right[c] = -1;
for (int j = 0; j < pat.length(); j++)
right[pat.charAt(j)] = j;
}
/**
* Preprocesses the pattern string.
*
* @param pattern
* the pattern string
* @param R
* the alphabet size
*/
public BoyerMoore(char[] pattern, int R) {
this.R = R;
this.pattern = new char[pattern.length];
for (int j = 0; j < pattern.length; j++)
this.pattern[j] = pattern[j];
// position of rightmost occurrence of c in the pattern
right = new int[R];
for (int c = 0; c < R; c++)
right[c] = -1;
for (int j = 0; j < pattern.length; j++)
right[pattern[j]] = j;
}
/**
* Returns the index of the first occurrrence of the pattern string in the text string.
*
* @param txt
* the text string
* @return the index of the first occurrence of the pattern string in the text string; n if no
* such match
*/
public int search(String txt) {
int m = pat.length();
int n = txt.length();
int skip;
for (int i = 0; i <= n - m; i += skip) {
skip = 0;
for (int j = m - 1; j >= 0; j--) {
if (pat.charAt(j) != txt.charAt(i + j)) {
skip = Math.max(1, j - right[txt.charAt(i + j)]);
break;
}
}
if (skip == 0)
return i; // found
}
return n; // not found
}
/**
* Returns the index of the first occurrrence of the pattern string in the text string.
*
* @param text
* the text string
* @return the index of the first occurrence of the pattern string in the text string; n if no
* such match
*/
public int search(char[] text) {
int m = pattern.length;
int n = text.length;
int skip;
for (int i = 0; i <= n - m; i += skip) {
skip = 0;
for (int j = m - 1; j >= 0; j--) {
if (pattern[j] != text[i + j]) {
skip = Math.max(1, j - right[text[i + j]]);
break;
}
}
if (skip == 0)
return i; // found
}
return n; // not found
}
}
Rabin-Karp fingerprint search
Basic idea is using modular hashing to compute a hash of pattern[0..M-1], for each i, compute a hash of text[i..M+i-1], if pattern hash = text substring hash, check for a match.
Module hash function covers: M-digit, base-R integer, and modulo Q.
- First M entries: Use Horner’s rule.
- Remaining entries: Use rolling hash (and % to avoid overflow).
The Monte Carlo version of Rabin-Karp substring search is linear-time and extremely likely to be correct. If you also add a check() to check that the text matches the pattern, which turns into the Las Vegas version.

public class RabinKarp {
private String pat; // the pattern // needed only for Las Vegas
private long patHash; // pattern hash value
private int m; // pattern length
private long q; // a large prime, small enough to avoid long overflow
private int R; // radix
private long RM; // R^(M-1) % Q
/**
* Preprocesses the pattern string.
*
* @param pattern
* the pattern string
* @param R
* the alphabet size
*/
public RabinKarp(char[] pattern, int R) {
this.pat = String.valueOf(pattern);
this.R = R;
throw new UnsupportedOperationException("Operation not supported yet");
}
/**
* Preprocesses the pattern string.
*
* @param pat
* the pattern string
*/
public RabinKarp(String pat) {
this.pat = pat; // save pattern (needed only for Las Vegas)
R = 256;
m = pat.length();
q = longRandomPrime();
// precompute R^(m-1) % q for use in removing leading digit
RM = 1;
for (int i = 1; i <= m - 1; i++)
RM = (R * RM) % q;
patHash = hash(pat, m);
}
// Compute hash for key[0..m-1].
private long hash(String key, int m) {
long h = 0;
for (int j = 0; j < m; j++)
h = (R * h + key.charAt(j)) % q;
return h;
}
// Las Vegas version: does pat[] match txt[i..i-m+1] ?
private boolean check(String txt, int i) {
for (int j = 0; j < m; j++)
if (pat.charAt(j) != txt.charAt(i + j))
return false;
return true;
}
// Monte Carlo version: always return true
// private boolean check(int i) {
// return true;
// }
/**
* Returns the index of the first occurrrence of the pattern string in the text string.
*
* @param txt
* the text string
* @return the index of the first occurrence of the pattern string in the text string; n if no
* such match
*/
public int search(String txt) {
int n = txt.length();
if (n < m)
return n;
long txtHash = hash(txt, m);
// check for match at offset 0
if ((patHash == txtHash) && check(txt, 0))
return 0;
// check for hash match; if hash match, check for exact match
for (int i = m; i < n; i++) {
// Remove leading digit, add trailing digit, check for match.
txtHash = (txtHash + q - RM * txt.charAt(i - m) % q) % q;
txtHash = (txtHash * R + txt.charAt(i)) % q;
// match
int offset = i - m + 1;
if ((patHash == txtHash) && check(txt, offset))
return offset;
}
// no match
return n;
}
// a random 31-bit prime
private static long longRandomPrime() {
BigInteger prime = BigInteger.probablePrime(31, new Random());
return prime.longValue();
}
}
Regular Expressions
email address [a-z]+@([a-z]+.)+(edu|com) rs@cs.princeton.edu
java identifier [$_A-Za-z][$_A-Za-z0-9]* testUser
Nondeterministic finite-state automata (NFA) can “guess” the right one when faced with more than one way to try to match the pattern. NFA is an abstract machine equivalent in power to RE. It supports the following operations: concatenation, closure, binary or, and parentheses…
- Build the NFA corresponding to the given RE.
- Maintain a stack.
- Add e-transition edges for closure/or.
- Takes time and space proportional to m in the worst case.
- Simulate the operation of that NFA on the given text.
- Determining whether an N-character text is recognized by the NFA corresponding to an M-character pattern takes time proportional to \(MN\) in the worst case.
- For each of the N text characters, we iterate through a set of states of size no more than M and run DFS on the graph of ε-transitions.
- Runs in time proportional to E + V.
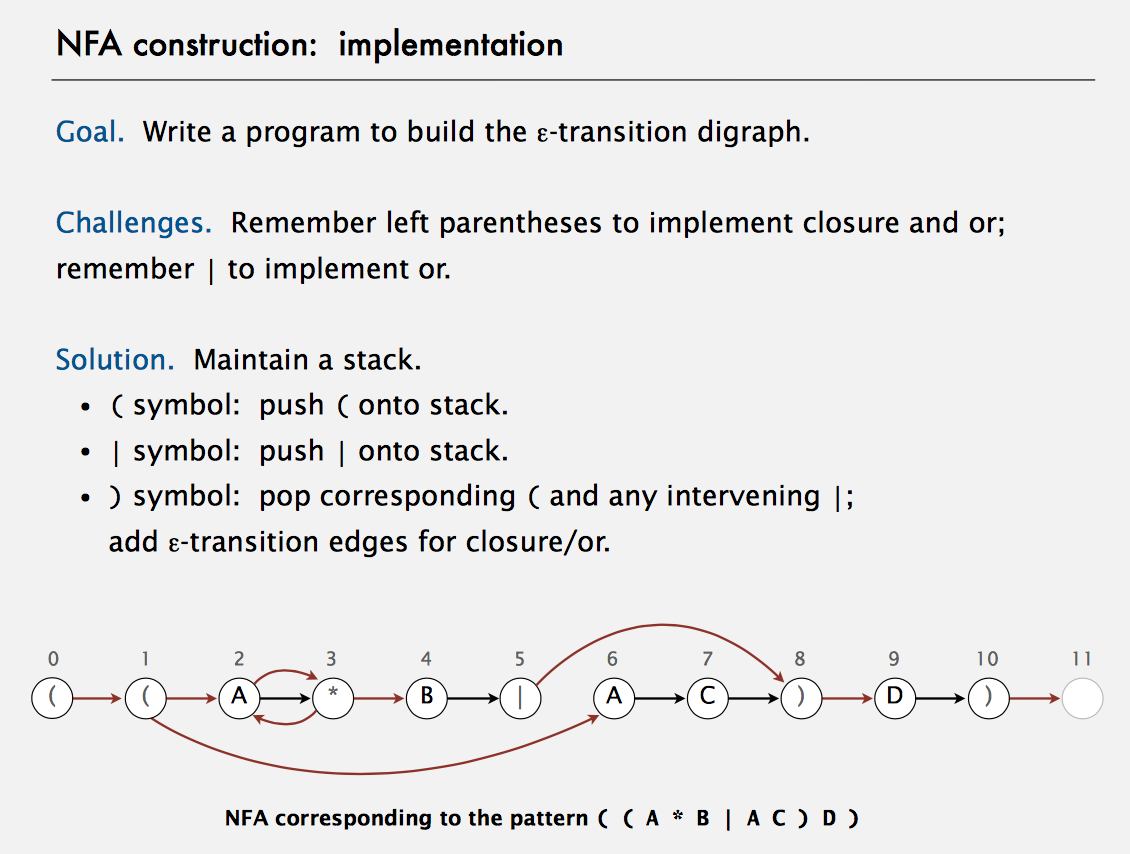
public class NFA {
private Digraph graph; // digraph of epsilon transitions
private String regexp; // regular expression
private final int m; // number of characters in regular expression
/**
* Initializes the NFA from the specified regular expression.
*/
public NFA(String regexp) {
this.regexp = regexp;
m = regexp.length();
Stack<Integer> ops = new Stack<Integer>();
graph = new Digraph(m + 1);
for (int i = 0; i < m; i++) {
int lp = i;
if (regexp.charAt(i) == '(' || regexp.charAt(i) == '|')
ops.push(i);
else if (regexp.charAt(i) == ')') {
int or = ops.pop();
// 2-way or operator
if (regexp.charAt(or) == '|') {
lp = ops.pop();
graph.addEdge(lp, or + 1);
graph.addEdge(or, i);
} else if (regexp.charAt(or) == '(')
lp = or;
else
assert false;
}
// closure operator (uses 1-character lookahead)
if (i < m - 1 && regexp.charAt(i + 1) == '*') {
graph.addEdge(lp, i + 1);
graph.addEdge(i + 1, lp);
}
if (regexp.charAt(i) == '(' || regexp.charAt(i) == '*' || regexp.charAt(i) == ')')
graph.addEdge(i, i + 1);
}
if (ops.size() != 0)
throw new IllegalArgumentException("Invalid regular expression");
}
/**
* Returns true if the text is matched by the regular expression.
*/
public boolean recognizes(String txt) {
DirectedDFS dfs = new DirectedDFS(graph, 0);
Bag<Integer> pc = new Bag<Integer>();
for (int v = 0; v < graph.V(); v++)
if (dfs.marked(v))
pc.add(v);
// Compute possible NFA states for txt[i+1]
for (int i = 0; i < txt.length(); i++) {
if (txt.charAt(i) == '*' || txt.charAt(i) == '|' || txt.charAt(i) == '(' || txt.charAt(i) == ')')
throw new IllegalArgumentException("text contains the metacharacter '" + txt.charAt(i) + "'");
Bag<Integer> match = new Bag<Integer>();
for (int v : pc) {
if (v == m)
continue;
if ((regexp.charAt(v) == txt.charAt(i)) || regexp.charAt(v) == '.')
match.add(v + 1);
}
dfs = new DirectedDFS(graph, match);
pc = new Bag<Integer>();
for (int v = 0; v < graph.V(); v++)
if (dfs.marked(v))
pc.add(v);
// optimization if no states reachable
if (pc.size() == 0)
return false;
}
// check for accept state
for (int v : pc)
if (v == m)
return true;
return false;
}
public class DirectedDFS {
// marked[v] = true if v is reachable from source (or sources)
private boolean[] marked;
private int count; // number of vertices reachable from s
public DirectedDFS(Digraph G, int s) {
marked = new boolean[G.V()];
validateVertex(s);
dfs(G, s);
}
public DirectedDFS(Digraph G, Iterable<Integer> sources) {
marked = new boolean[G.V()];
validateVertices(sources);
for (int v : sources) {
if (!marked[v])
dfs(G, v);
}
}
private void dfs(Digraph G, int v) {
count++;
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w])
dfs(G, w);
}
}
public boolean marked(int v) {
validateVertex(v);
return marked[v];
}
private void validateVertex(int v) {
int V = marked.length;
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
private void validateVertices(Iterable<Integer> vertices) {
if (vertices == null) {
throw new IllegalArgumentException("argument is null");
}
int V = marked.length;
for (int v : vertices) {
if (v < 0 || v >= V) {
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
}
}
}
}
}
Data Compression
Compression reduces the size of a file:
- To save space when storing it;
- To save time when transmitting it;
- Most files have lots of redundancy
No algorithm can compress every bitstring.
- By contradiction, all bitstrings can be compressed to 0 bits!
- By counting, Only 1 + 2 + 4 + … + 2^998 + 2^999 can be encoded with <= 999 bits.
The lossless compression methods must be oriented toward taking advantage of known structure in the bitstreams to be compressed.
- Small alphabets
- Long sequences of identical bits/characters
- Frequently used characters
- Long reused bit/character sequences
Binary Reader
public final class BinaryStdIn {
private static final int EOF = -1; // end of file
private static BufferedInputStream in; // input stream
private static int buffer; // one character buffer
private static int n; // number of bits left in buffer
private static boolean isInitialized; // has BinaryStdIn been called for first time?
// don't instantiate
private BinaryStdIn() {
}
// fill buffer
private static void initialize() {
in = new BufferedInputStream(System.in);
buffer = 0;
n = 0;
fillBuffer();
isInitialized = true;
}
private static void fillBuffer() {
try {
buffer = in.read();
n = 8;
} catch (IOException e) {
System.out.println("EOF");
buffer = EOF;
n = -1;
}
}
/**
* Close this input stream and release any associated system resources.
*/
public static void close() {
if (!isInitialized)
initialize();
try {
in.close();
isInitialized = false;
} catch (IOException ioe) {
throw new IllegalStateException("Could not close BinaryStdIn", ioe);
}
}
/**
* Returns true if standard input is empty.
*/
public static boolean isEmpty() {
if (!isInitialized)
initialize();
return buffer == EOF;
}
/**
* Reads the next bit of data from standard input and return as a boolean.
*/
public static boolean readBoolean() {
if (isEmpty())
throw new NoSuchElementException("Reading from empty input stream");
n--;
boolean bit = ((buffer >> n) & 1) == 1;
if (n == 0)
fillBuffer();
return bit;
}
/**
* Reads the next 8 bits from standard input and return as an 8-bit char. Note that {@code char} is a 16-bit type; to read the next 16 bits as a char, use {@code readChar(16)}.
*/
public static char readChar() {
if (isEmpty())
throw new NoSuchElementException("Reading from empty input stream");
// special case when aligned byte
if (n == 8) {
int x = buffer;
fillBuffer();
return (char) (x & 0xff);
}
// combine last n bits of current buffer with first 8-n bits of new buffer
int x = buffer;
x <<= (8 - n);
int oldN = n;
fillBuffer();
if (isEmpty())
throw new NoSuchElementException("Reading from empty input stream");
n = oldN;
x |= (buffer >>> n);
return (char) (x & 0xff);
// the above code doesn't quite work for the last character if n = 8
// because buffer will be -1, so there is a special case for aligned byte
}
/**
* Reads the next r bits from standard input and return as an r-bit character.
*/
public static char readChar(int r) {
if (r < 1 || r > 16)
throw new IllegalArgumentException("Illegal value of r = " + r);
// optimize r = 8 case
if (r == 8)
return readChar();
char x = 0;
for (int i = 0; i < r; i++) {
x <<= 1;
boolean bit = readBoolean();
if (bit)
x |= 1;
}
return x;
}
/**
* Reads the remaining bytes of data from standard input and return as a string.
*/
public static String readString() {
if (isEmpty())
throw new NoSuchElementException("Reading from empty input stream");
StringBuilder sb = new StringBuilder();
while (!isEmpty()) {
char c = readChar();
sb.append(c);
}
return sb.toString();
}
/**
* Reads the next 16 bits from standard input and return as a 16-bit short.
*/
public static short readShort() {
short x = 0;
for (int i = 0; i < 2; i++) {
char c = readChar();
x <<= 8;
x |= c;
}
return x;
}
/**
* Reads the next 32 bits from standard input and return as a 32-bit int.
*/
public static int readInt() {
int x = 0;
for (int i = 0; i < 4; i++) {
char c = readChar();
x <<= 8;
x |= c;
}
return x;
}
/**
* Reads the next r bits from standard input and return as an r-bit int.
*/
public static int readInt(int r) {
if (r < 1 || r > 32)
throw new IllegalArgumentException("Illegal value of r = " + r);
// optimize r = 32 case
if (r == 32)
return readInt();
int x = 0;
for (int i = 0; i < r; i++) {
x <<= 1;
boolean bit = readBoolean();
if (bit)
x |= 1;
}
return x;
}
/**
* Reads the next 64 bits from standard input and return as a 64-bit long.
*/
public static long readLong() {
long x = 0;
for (int i = 0; i < 8; i++) {
char c = readChar();
x <<= 8;
x |= c;
}
return x;
}
/**
* Reads the next 64 bits from standard input and return as a 64-bit double.
*/
public static double readDouble() {
return Double.longBitsToDouble(readLong());
}
/**
* Reads the next 32 bits from standard input and return as a 32-bit float.
*/
public static float readFloat() {
return Float.intBitsToFloat(readInt());
}
/**
* Reads the next 8 bits from standard input and return as an 8-bit byte.
*/
public static byte readByte() {
char c = readChar();
return (byte) (c & 0xff);
}
public static void main(String[] args) {
// read one 8-bit char at a time
while (!BinaryStdIn.isEmpty()) {
char c = BinaryStdIn.readChar();
BinaryStdOut.write(c);
}
BinaryStdOut.flush();
}
}
Binary Writer
public final class BinaryStdOut {
private static BufferedOutputStream out; // output stream (standard output)
private static int buffer; // 8-bit buffer of bits to write
private static int n; // number of bits remaining in buffer
private static boolean isInitialized; // has BinaryStdOut been called for first time?
// don't instantiate
private BinaryStdOut() {
}
// initialize BinaryStdOut
private static void initialize() {
out = new BufferedOutputStream(System.out);
buffer = 0;
n = 0;
isInitialized = true;
}
/**
* Writes the specified bit to standard output.
*/
private static void writeBit(boolean bit) {
if (!isInitialized)
initialize();
// add bit to buffer
buffer <<= 1;
if (bit)
buffer |= 1;
// if buffer is full (8 bits), write out as a single byte
n++;
if (n == 8)
clearBuffer();
}
/**
* Writes the 8-bit byte to standard output.
*/
private static void writeByte(int x) {
if (!isInitialized)
initialize();
assert x >= 0 && x < 256;
// optimized if byte-aligned
if (n == 0) {
try {
out.write(x);
} catch (IOException e) {
e.printStackTrace();
}
return;
}
// otherwise write one bit at a time
for (int i = 0; i < 8; i++) {
boolean bit = ((x >>> (8 - i - 1)) & 1) == 1;
writeBit(bit);
}
}
// write out any remaining bits in buffer to standard output, padding with 0s
private static void clearBuffer() {
if (!isInitialized)
initialize();
if (n == 0)
return;
if (n > 0)
buffer <<= (8 - n); // add padding
try {
out.write(buffer);
} catch (IOException e) {
e.printStackTrace();
}
n = 0;
buffer = 0;
}
/**
* Flushes standard output, padding 0s if number of bits written so far is not a multiple of 8.
*/
public static void flush() {
clearBuffer();
try {
out.flush();
} catch (IOException e) {
e.printStackTrace();
}
}
/**
* Flushes and closes standard output. Once standard output is closed, you can no longer write bits to it.
*/
public static void close() {
flush();
try {
out.close();
isInitialized = false;
} catch (IOException e) {
e.printStackTrace();
}
}
/**
* Writes the specified bit to standard output.
*
* @param x
* the {@code boolean} to write.
*/
public static void write(boolean x) {
writeBit(x);
}
/**
* Writes the 8-bit byte to standard output.
*
* @param x
* the {@code byte} to write.
*/
public static void write(byte x) {
writeByte(x & 0xff);
}
/**
* Writes the 32-bit int to standard output.
*/
public static void write(int x) {
writeByte((x >>> 24) & 0xff);
writeByte((x >>> 16) & 0xff);
writeByte((x >>> 8) & 0xff);
writeByte((x >>> 0) & 0xff);
}
/**
* Writes the r-bit int to standard output.
*/
public static void write(int x, int r) {
if (r == 32) {
write(x);
return;
}
if (r < 1 || r > 32)
throw new IllegalArgumentException("Illegal value for r = " + r);
if (x < 0 || x >= (1 << r))
throw new IllegalArgumentException("Illegal " + r + "-bit char = " + x);
for (int i = 0; i < r; i++) {
boolean bit = ((x >>> (r - i - 1)) & 1) == 1;
writeBit(bit);
}
}
/**
* Writes the 64-bit double to standard output.
*/
public static void write(double x) {
write(Double.doubleToRawLongBits(x));
}
/**
* Writes the 64-bit long to standard output.
*/
public static void write(long x) {
writeByte((int) ((x >>> 56) & 0xff));
writeByte((int) ((x >>> 48) & 0xff));
writeByte((int) ((x >>> 40) & 0xff));
writeByte((int) ((x >>> 32) & 0xff));
writeByte((int) ((x >>> 24) & 0xff));
writeByte((int) ((x >>> 16) & 0xff));
writeByte((int) ((x >>> 8) & 0xff));
writeByte((int) ((x >>> 0) & 0xff));
}
/**
* Writes the 32-bit float to standard output.
*/
public static void write(float x) {
write(Float.floatToRawIntBits(x));
}
/**
* Writes the 16-bit int to standard output.
*/
public static void write(short x) {
writeByte((x >>> 8) & 0xff);
writeByte((x >>> 0) & 0xff);
}
/**
* Writes the 8-bit char to standard output.
*/
public static void write(char x) {
if (x < 0 || x >= 256)
throw new IllegalArgumentException("Illegal 8-bit char = " + x);
writeByte(x);
}
/**
* Writes the r-bit char to standard output.
*/
public static void write(char x, int r) {
if (r == 8) {
write(x);
return;
}
if (r < 1 || r > 16)
throw new IllegalArgumentException("Illegal value for r = " + r);
if (x >= (1 << r))
throw new IllegalArgumentException("Illegal " + r + "-bit char = " + x);
for (int i = 0; i < r; i++) {
boolean bit = ((x >>> (r - i - 1)) & 1) == 1;
writeBit(bit);
}
}
/**
* Writes the string of 8-bit characters to standard output.
*/
public static void write(String s) {
for (int i = 0; i < s.length(); i++)
write(s.charAt(i));
}
/**
* Writes the string of r-bit characters to standard output.
*/
public static void write(String s, int r) {
for (int i = 0; i < s.length(); i++)
write(s.charAt(i), r);
}
/**
* Tests the methods in this class.
*/
public static void main(String[] args) {
int m = Integer.parseInt(args[0]);
// write n integers to binary standard output
for (int i = 0; i < m; i++) {
BinaryStdOut.write(i);
}
BinaryStdOut.flush();
}
}
Fixed-length Codes
Example: Encode an N-character genome: A T A G A T G C A T A G…
We can code the 8 bits ASCII to 2 bits, like A: (01000001) to (00); C: (01000011) to (01)…
Need ceil (lgR) bits to specify one of R symbols.
Run-length Encoding
Example: Simple type of redundancy in a bitstream. Long runs of repeated bits.
0000000000000001111111000000011111111111
We can use 4-bit counts to represent alternating runs of 0s and 1s: 15 0s, then 7 1s, then 7 0s, then 11 1s.
1111 0111 0111 1011
public class RunLength {
private static final int R = 256;
private static final int LG_R = 8;
/**
* Reads a sequence of bits from standard input (that are encoded using run-length encoding with 8-bit run lengths); decodes them; and writes the results to standard output.
*/
public static void expand() {
boolean b = false;
while (!BinaryStdIn.isEmpty()) {
int run = BinaryStdIn.readInt(LG_R);
for (int i = 0; i < run; i++)
BinaryStdOut.write(b);
b = !b;
}
BinaryStdOut.close();
}
public static void expand2() {
boolean b = false;
while (!BinaryStdIn.isEmpty()) {
int run = BinaryStdIn.readInt(LG_R);
for (int i = 0; i < run; i++) {
BinaryStdOut.write(b);
}
b = !b;
}
BinaryStdOut.close();
}
/**
* Reads a sequence of bits from standard input; compresses them using run-length coding with 8-bit run lengths; and writes the results to standard output.
*/
public static void compress() {
char run = 0;
boolean old = false;
while (!BinaryStdIn.isEmpty()) {
boolean b = BinaryStdIn.readBoolean();
if (b != old) {
BinaryStdOut.write(run, LG_R);
run = 1;
old = !old;
} else {
if (run == R - 1) {
BinaryStdOut.write(run, LG_R);
run = 0;
BinaryStdOut.write(run, LG_R);
}
run++;
}
}
BinaryStdOut.write(run, LG_R);
BinaryStdOut.close();
}
public static void write(char x, int r) {
if (r < 1 || r > 16)
throw new IllegalArgumentException("Illegal value for r = " + r);
if (x >= (1 << r))
throw new IllegalArgumentException("Illegal " + r + "-bit char = " + x);
for (int i = 0; i < r; i++) {
boolean bit = ((x >>> (r - i - 1)) & 1) == 1;
writeBit(bit);
}
}
}
Huffman Compression
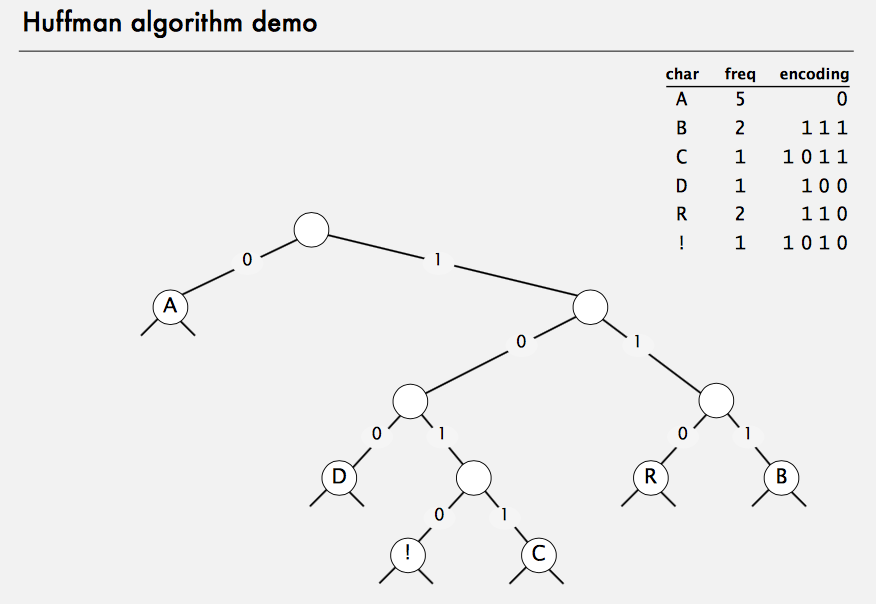
Huffman compression implementation:
To compress it:
- Read the input.
- Tabulate the frequency of occurrence of each char value in the input.
- Build the Huffman encoding trie corresponding to those frequencies.
- Build the corresponding codeword table, to associate a bitstring with each char value in the input.
- Write the trie, encoded as a bitstring (pre-order traverse).
- Write the count of characters in the input, encoded as a bitstring.
- Use the codeword table to write the codeword for each input character.
To expand a bitstream:
- Read the trie (encoded at the beginning of the bitstream).
- Read the count of characters to be decoded.
- Use the trie to decode the bitstream.
Huffman compression handles variable-length prefix-free codes. It is effective for various types of files, not just natural language text.
Running time with a binary heap is \(N + R\log R\).
public class Huffman {
// alphabet size of extended ASCII
private static final int R = 256;
// Do not instantiate.
private Huffman() {
}
// Huffman trie node
private static class Node implements Comparable<Node> {
private final char ch;
private final int freq;
private final Node left, right;
Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
// is the node a leaf node?
private boolean isLeaf() {
assert ((left == null) && (right == null)) || ((left != null) && (right != null));
return (left == null) && (right == null);
}
// compare, based on frequency
public int compareTo(Node that) {
return this.freq - that.freq;
}
}
/**
* Reads a sequence of 8-bit bytes from standard input; compresses them using Huffman codes with an 8-bit alphabet; and writes the results to standard output.
*/
public static void compress() {
// read the input
String s = BinaryStdIn.readString();
char[] input = s.toCharArray();
// tabulate frequency counts
int[] freq = new int[R];
for (int i = 0; i < input.length; i++)
freq[input[i]]++;
// build Huffman trie
Node root = buildTrie(freq);
// build code table
String[] st = new String[R];
buildCode(st, root, "");
// print trie for decoder
writeTrie(root);
// print number of bytes in original uncompressed message
BinaryStdOut.write(input.length);
// use Huffman code to encode input
for (int i = 0; i < input.length; i++) {
String code = st[input[i]];
for (int j = 0; j < code.length(); j++) {
if (code.charAt(j) == '0') {
BinaryStdOut.write(false);
} else if (code.charAt(j) == '1') {
BinaryStdOut.write(true);
} else
throw new IllegalStateException("Illegal state");
}
}
// close output stream
BinaryStdOut.close();
}
// build the Huffman trie given frequencies
private static Node buildTrie(int[] freq) {
// initialze priority queue with singleton trees
MinPQ<Node> pq = new MinPQ<Node>();
for (char i = 0; i < R; i++)
if (freq[i] > 0)
pq.insert(new Node(i, freq[i], null, null));
// special case in case there is only one character with a nonzero frequency
if (pq.size() == 1) {
if (freq['\0'] == 0)
pq.insert(new Node('\0', 0, null, null));
else
pq.insert(new Node('\1', 0, null, null));
}
// merge two smallest trees
while (pq.size() > 1) {
Node left = pq.delMin();
Node right = pq.delMin();
Node parent = new Node('\0', left.freq + right.freq, left, right);
pq.insert(parent);
}
return pq.delMin();
}
// write bitstring-encoded trie to standard output
private static void writeTrie(Node x) {
if (x.isLeaf()) {
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch, 8);
return;
}
BinaryStdOut.write(false);
writeTrie(x.left);
writeTrie(x.right);
}
// make a lookup table from symbols and their encodings
private static void buildCode(String[] st, Node x, String s) {
if (!x.isLeaf()) {
buildCode(st, x.left, s + '0');
buildCode(st, x.right, s + '1');
} else {
st[x.ch] = s;
}
}
/**
* Reads a sequence of bits that represents a Huffman-compressed message from standard input; expands them; and writes the results to standard output.
*/
public static void expand() {
// read in Huffman trie from input stream
Node root = readTrie();
// number of bytes to write
int length = BinaryStdIn.readInt();
// decode using the Huffman trie
for (int i = 0; i < length; i++) {
Node x = root;
while (!x.isLeaf()) {
boolean bit = BinaryStdIn.readBoolean();
if (bit)
x = x.right;
else
x = x.left;
}
BinaryStdOut.write(x.ch, 8);
}
BinaryStdOut.close();
}
private static Node readTrie() {
boolean isLeaf = BinaryStdIn.readBoolean();
if (isLeaf) {
return new Node(BinaryStdIn.readChar(), -1, null, null);
} else {
return new Node('\0', -1, readTrie(), readTrie());
}
}
/**
* Sample client that calls {@code compress()} if the command-line argument is "-" an {@code expand()} if it is "+".
*/
public static void main(String[] args) {
if (args[0].equals("-"))
compress();
else if (args[0].equals("+"))
expand();
else
throw new IllegalArgumentException("Illegal command line argument");
}
}
LZW Compression
Summary: Huffman does variable length code for fixed length symbols; LZW does fixed length code for variable length strings.
Using prefix match code (Ternary Search Trie) to implements LZW compression: Encode everything in binary; Limit the number of elements in the symbol table; Initially dictionary has 512 elements (with 256 elements filled in for ASCII characters), transmit 9 bits per integer. When it is filled up, we double it to 1024 and start transmitting 10 bits per integer.
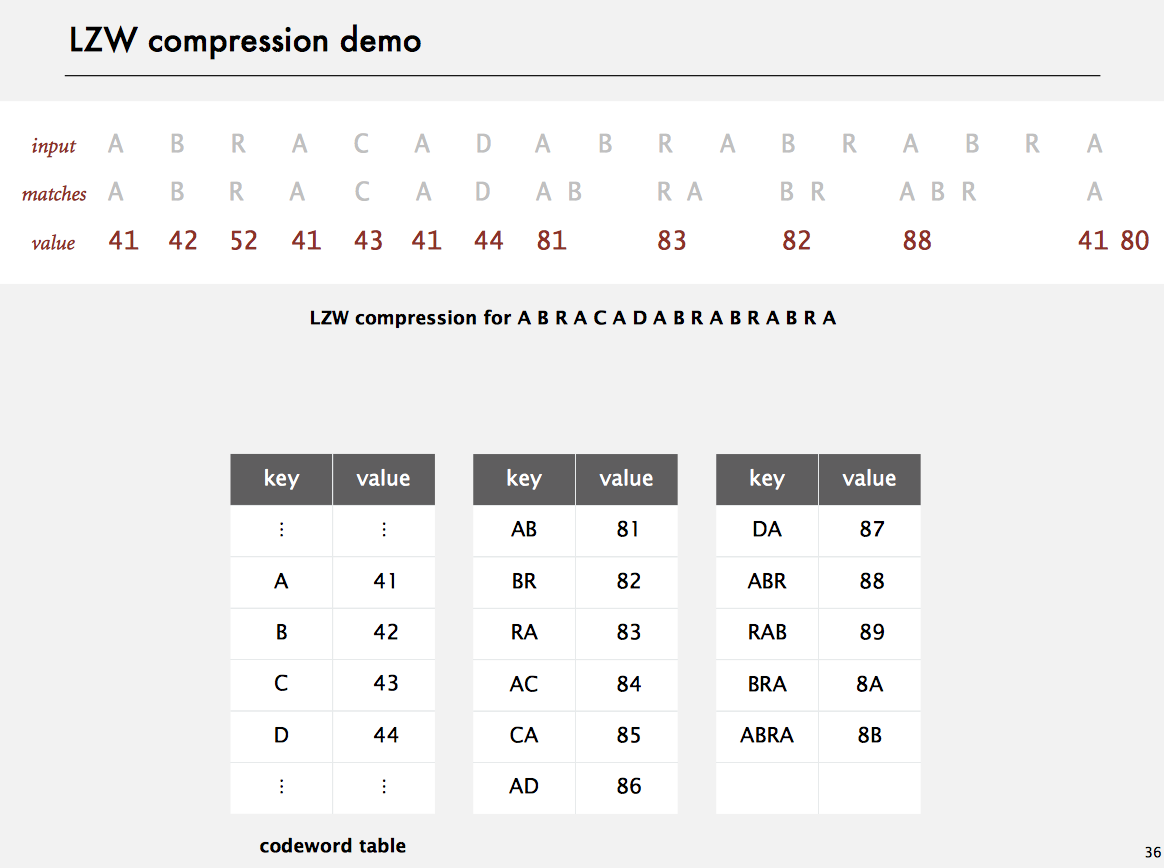
LZW Compression:
- Create TST associating W-bit codewords with string keys.
- Initialize ST with codewords for single-char keys.
- Find longest string s in TST that is a prefix of unscanned part of input.
- Write the W-bit codeword associated with s.
- Add s + c to TST, where c is next char in the input.
LZW Expansion:
- Create ST associating string values with W-bit keys.
- Initialize ST to contain single-char values.
- Read a W-bit key.
- Find associated string value in ST and write it out.
- Update ST.
public class LZW {
private static final int R = 256; // number of input chars
private static final int L = 4096; // number of codewords = 2^W
private static final int W = 12; // codeword width
/**
* Reads a sequence of 8-bit bytes from standard input; compresses
* them using LZW compression with 12-bit codewords; and writes the results
* to standard output.
*/
public static void compress() {
String input = BinaryStdIn.readString();
TST<Integer> st = new TST<Integer>();
for (int i = 0; i < R; i++)
st.put("" + (char) i, i);
int code = R+1; // R is codeword for EOF
while (input.length() > 0) {
String s = st.longestPrefixOf(input); // Find max prefix match s.
BinaryStdOut.write(st.get(s), W); // Print s's encoding.
int t = s.length();
if (t < input.length() && code < L) // Add s to symbol table.
st.put(input.substring(0, t + 1), code++);
input = input.substring(t); // Scan past s in input.
}
BinaryStdOut.write(R, W);
BinaryStdOut.close();
}
/**
* Reads a sequence of bit encoded using LZW compression with
* 12-bit codewords from standard input; expands them; and writes
* the results to standard output.
*/
public static void expand() {
String[] st = new String[L];
int i; // next available codeword value
// initialize symbol table with all 1-character strings
for (i = 0; i < R; i++)
st[i] = "" + (char) i;
st[i++] = ""; // (unused) lookahead for EOF
int codeword = BinaryStdIn.readInt(W);
if (codeword == R) return; // expanded message is empty string
String val = st[codeword];
while (true) {
BinaryStdOut.write(val);
codeword = BinaryStdIn.readInt(W);
if (codeword == R) break;
String s = st[codeword];
if (i == codeword) s = val + val.charAt(0); // special case hack
if (i < L) st[i++] = val + s.charAt(0);
val = s;
}
BinaryStdOut.close();
}
}